Lecture 24: The Human Eye

25.2, 25.7, 25.9

cornea

does most of the focusing (70%)

R = 8 mm, n = 1.376

Iris

controls light entering the eye

Lens

does fine adjustment to focusing by adjusting its own focal length

n = 1.386 - 1.406

retina - rods and cones

converts light into electrical impulses

optic nerve → brain → image

fovea

most sensitive part of retina

0.25 mm in diameter

consists of closely packed cones

the human eye resembles…

a camera in its basic functioning, with an adjustable lens, the iris and the retina

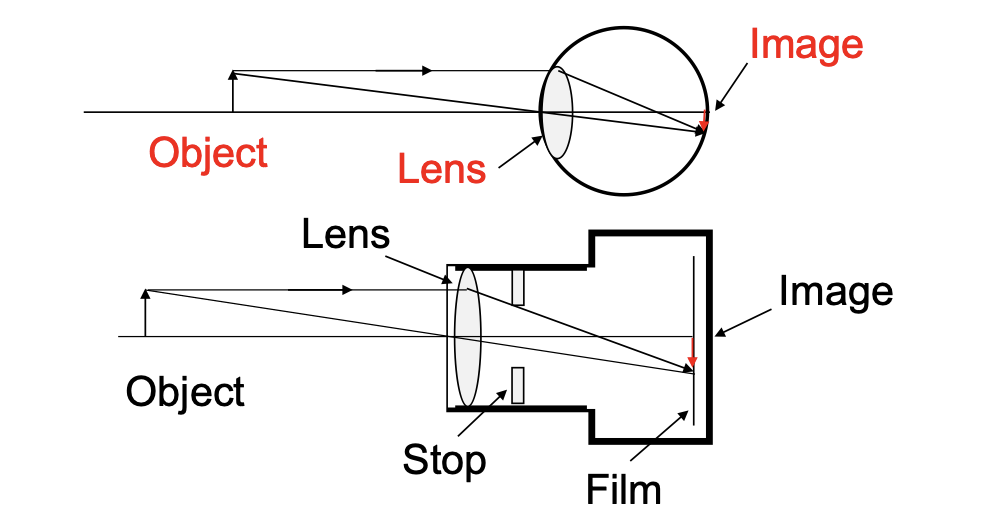
accomodation by a normal eye

• most of the focusing action occurs at the cornea due to refraction

• the lens does fine adjustment to focusing by varying its own focal length by changing its thickness by relaxing or contracting ciliary muscles

• this focusing adjustment is called accommodation

when we see object at infinity, the eye lens is relaxed and thinner….

hence its f is large

when we see nearby object, the eye lens is thickened…

hence its f is small

what is the range length of the eye lens from far point to the near point for a normal eye, assume diameter of the eyeball = 2cm

1/do + 1/di = 1/f

1/infinity + 1/2 = 1/f

f = 2cm

when object is at near point = 25 cm

1/do + 1/di = 1/f

1/25 + ½ = 1/f

f = 1.85 cm

2-1.85 = 0.15 cm → focal length

near point

closest distance at which eye can focus clearly, for eye it is about 25 cm

far point

farthest distance at which eye can focus clearly, for normal eye it is at infinity

nearsightedness

far point of the eye comes closer to eye. So person can’t see distant objects clearly

farsightedness

near point is too far away from eye. So person can’t see near objects clearly

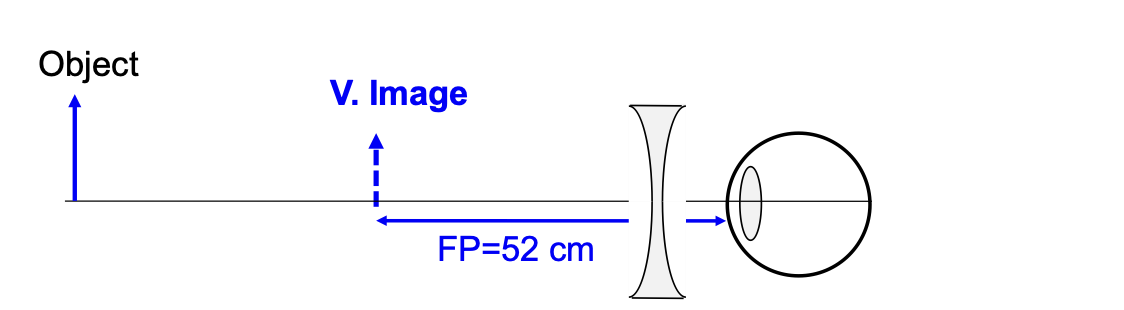
a nearsighted person has a far point of 52cm, calculate power of lens needed so that person can see distant objects clearly. Assume glasses are worn 2cm in front of the eye

do = infinity

di = -(52-2)=-50

1/do + 1/di = 1/f

f = -50 cm

P = 1/f → 1/-0.5 m = -2 diopter

diverging lens is used to correct nearsightedness

A farsighted person has a near point distance of 45 cm.

Calculate power of the lens needed so that person can read

newspaper held at 25 cm from the eye. Assume glasses are worn

2.0 cm in front of the eye.

do = 25 - 2 = 23

di = -(45-2) = - 43

1/do + 1/di = 1/f

f = 49.45 cm

Power = 1/f = 1/0.495

= +2 diopter

converging lens is used to correct farsightedness

when eyes are opened under water, objects appear blurred, why is this

because light rays are bent much less than they would, if entering the eye from air, hence are not focused on the retina, this can be avoided by wearing goggles

f(in water) > f(in air)

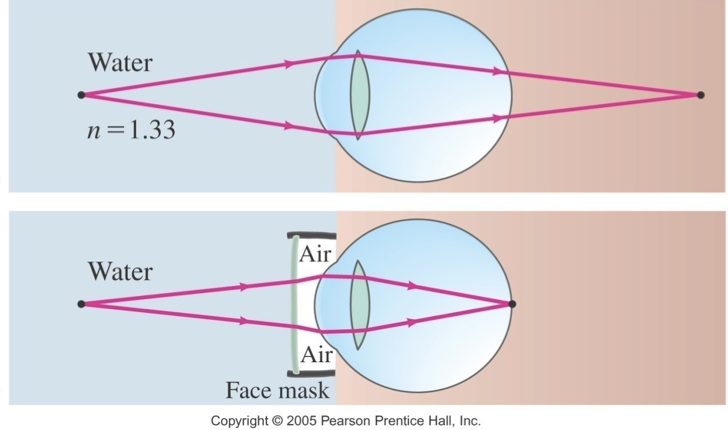
by how much the converging power of the cornea is reduced under water

nc / nw = 1.376/1.333 =1.0323 1.032

therefore, reduced by 3%

what happens when a person uses goggles

nc/n(air) = 1.376/1.000 =1.376 1.376

focusing action is restored to 100%

resolution

the ability of an instrument (eg. camera, telescope, lens) to produce distinct images of two closely spaced point objects

high resolution

closer images, yet distinct

factor that puts limit on resolution

the images formed are not point images, but are blob images use to diffraction effects

effect of diffraction of light

for a circular aperture of diameter D, the central maximum has an angular width theta

theta = 1.22wavelength/D

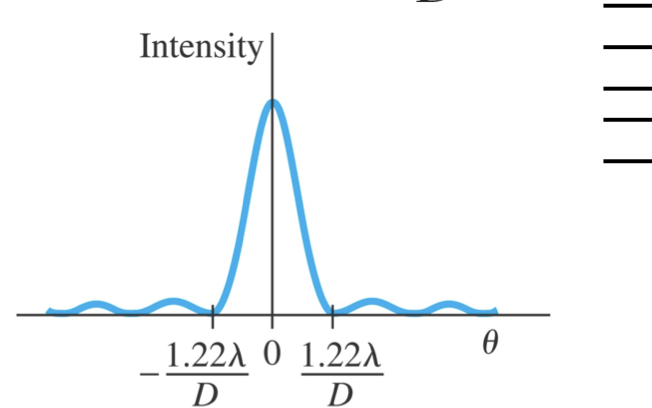
the Rayleigh criterion states that…

two images are just resolvable when the centre of one peak is over the first minimum of the other

youre in a plane at altitude of 10 000 ,, if you look down at the ground, estimate the minimum separation between objects that you could distinguish. Consider only diffraction effects. Assume diameter of your pupil, D = 3 mm and wavelength of 550 nm

theta = 1.22 wavelength/D

theta = distance/d

distance = theta x d

1.22(550×10^-9)/(3×10^-3) x 10 000

= 2.2 m

the net result is that the eye can resolve objects whose angular separation is about

5 × 10^-4 radian

minimum distance between two objects held at NP (25cm) that normal human eye can resolve? Assuming the angular limit of resolution is 5 × 10^-4 radian

angular limit of resolution

theta = 5 × 10^-4 rad

since theta = distance/L

distance = L x theta

(25 × 10^-2 m)(5 × 10^-4 rad)

x = 0.125 mm