Circular Motion

how to solve for non-uniform circular motion

draw a freebody diagram + use the forces to show a net force (fnet = force up - force down). Input in these values and rearrange

• top of circle on inside of rollercoaster/ at top of string:

  fnet = weight + tension/normal (both down)

  mv²/r=mg → v=√gr for MIN velocity at top

• bottom of circle:

  fnet = tension/normal - weight

• top of circle on outside of rollercoaster:

  fnet = weight - normal

can also use conservation of energy to find velocity in worst-case (using it with reference to the top because generally v=√gr)

real weight vs apparent weight

real weight = true weight = mg —> never changes

apparent weight is how heavy you feel based on the forces acting on you

—> weightless = you are in freefall

• No acceleration

  fnet = 0, you feel your real weight

• Accelerating up

  fnet = N - mg —> N = ma + mg, you feel heavier

• Accelerating down

  fnet = mg + N —> N = ma-mg, you feel lighter

Characteristics of UCM

• radius is constant

• period is constant

• speed is same

• direction if linear velocity is tangential to force

• acceleration/fnet is towards the centre (centripetal) + is constant

• angular velocity is constant

formula for UCM characteristics

• not if F = MAc is not exact, the object will not execute UCM

  F < MAc = slip out of turn

  F > MAc = slip into turn

• angular velocity must be in rad/s

  RPM is bigger than rad/s:

  RPM —> Rad/s = x (2𝜋/60)

  Rads —> RPM = ÷(2𝜋/60)

  for hertz:

  f —> t —> 2 pie / T

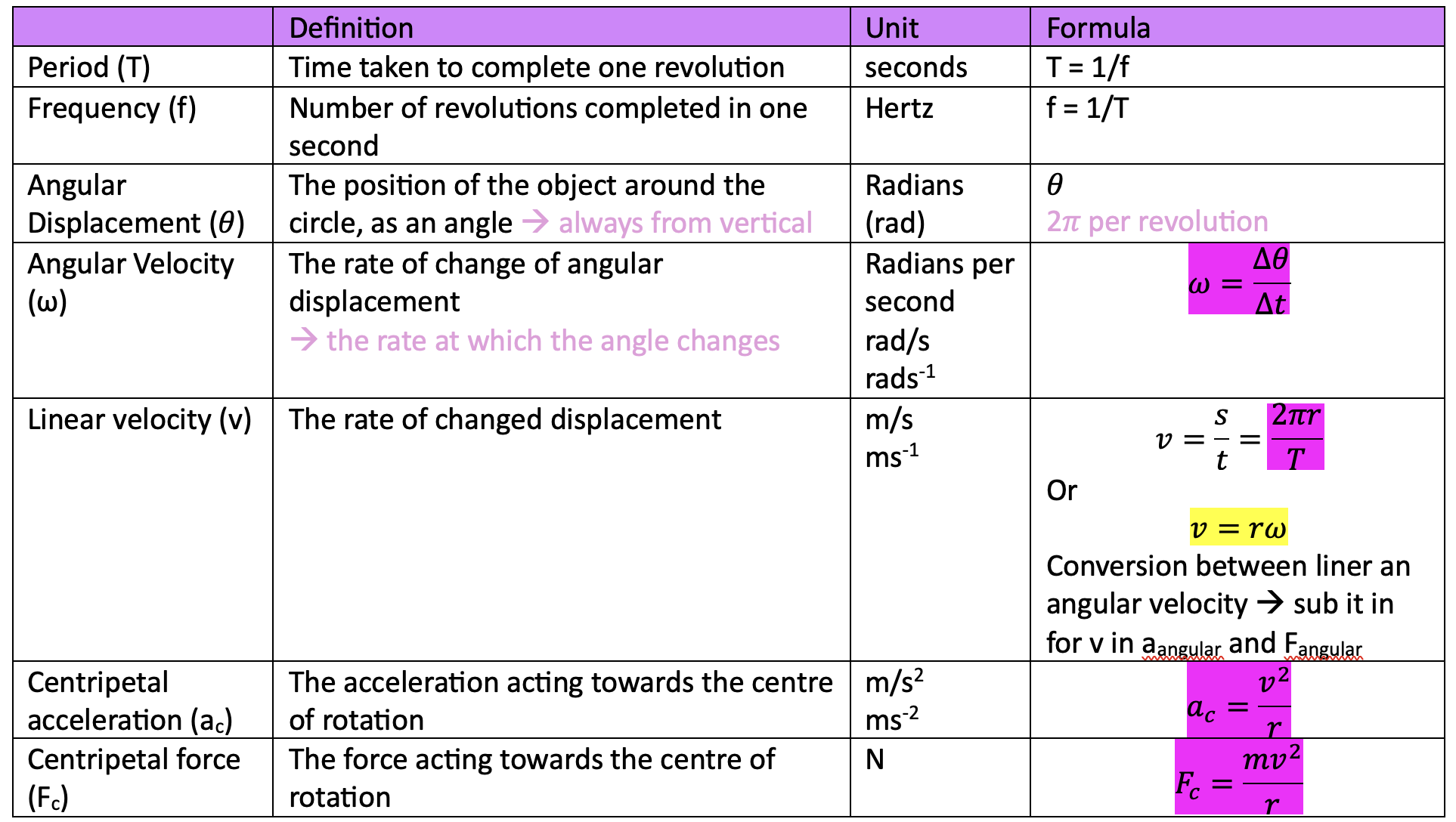
relationship between variables in Fc equation

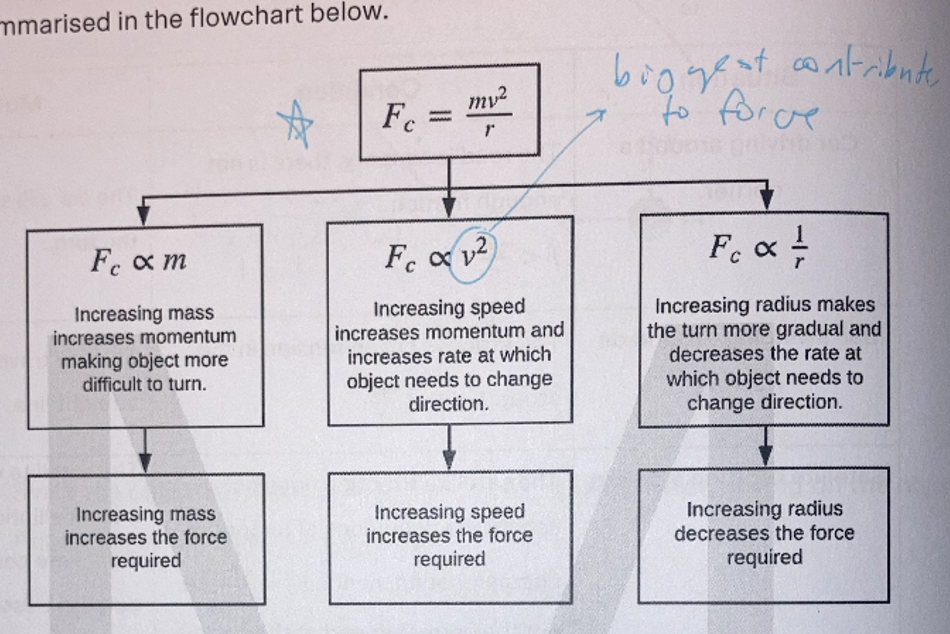
solving UCM for car on flat road

provider: friction

1. draw freebody diagram

   1. mg = N

   2. Fc = friction = 𝜇N = mv²/r

2. solve for unknowns

   1. If looking for acceleration, use Fnet = ma

      E.g. 𝜇N = (mv²/r ∴ v=√μgr

   2. If looking for velocity, use Fnet = (mv²/r

      E.g. a = 𝜇N ÷ m

solving UCM for car on banked road (no friction)

Provider = horizontal component of the normal force

1. freebody diagram

   1. normal force

   2. weight force

2. Decompose the normal force into vertical and horizontal components

   Nx = Nsin𝜃, Ny = Ncos𝜃

3. Apply N2L

   y: Fnet = 0, Ny = Ncos𝜃 = mg (eq 1)

   x: Nx = Nsin𝜃 = ma (eq 2) = mgtan𝜃

4. Solve simeltaneously by dividing eq 2 and 1

   1. tanW = a/g

   2. a=v²/r=gtanθ ∴v=√grtanθ

5. Find the normal force

   Can use pythag

   N =mg/cosθ

solving UCM for car on banked road (friction)

provider: x component of normal and friction —> friction generally goes DOWN THE SLOPE

1. freebody diagram

   1. normal

   2. weight

   3. friction

2. decompose normal and friction into vertical and horizontal components

   1. y: Ncosθ = mg+Fsinθ

   2. x: Fc = mv²/r = Nsinθ+Fcosθ

3. Solve simeltaneously by rearranging for m in y and substituting it in for x

4. rearrange for v

5. substitute friction in for μN so:

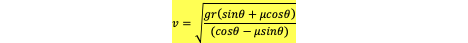
a mass on a string

provider: x component of tension

1. freebody (mg and tension)

2. decompose tension

   1. a. Tx = Tsin𝜃, Ty = Tcos𝜃 → Theta is always from the vertical

3. Apply N2L

   y: Fnet = 0, Ty = Tcos𝜃 = mg (eq 1)

   x: Tx = Tsin𝜃 = ma (eq 2) = mgtan𝜃

4. solve simeltaneously by diving eq 2 by 1

5. find acceleration and velocity:

   

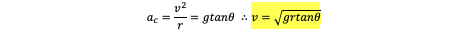
6. find tension

   Can use pythag

   T=mg/cosθ

period of a conical pendulum

work in UCM

none

No work is done when an object is in uniform circular motion (for any plane)

• Since the speed is not changing, the kinetic energy stays the same

• Since F and s are tangential (are perpendicular), work = 0

THERE IS NO WORK DONE IN A VERTICAL PLANE → BUT THE MECHANICAL ENERGY (U) IS CHANGING

torque

a measure of the force that can cause an object to rotate about an axis —> ROTATIONAL FORCE

• max when r and F are perpendicular (sin90 = 1)

• Torque is a vector

  • anticlockwise (-) and clockwise (+)

  • they can add

τ=r⊥ F=rF sin⁡θ —> theta is angle between vectors

for a rigid body, torque is constant so:

τ=r1⊥ F1 =r2⊥ F2

→ solve torque by decomposing F/r to and multiply it by the perpendicular component to r/F