AP CALCULUS AB

Trig Identities

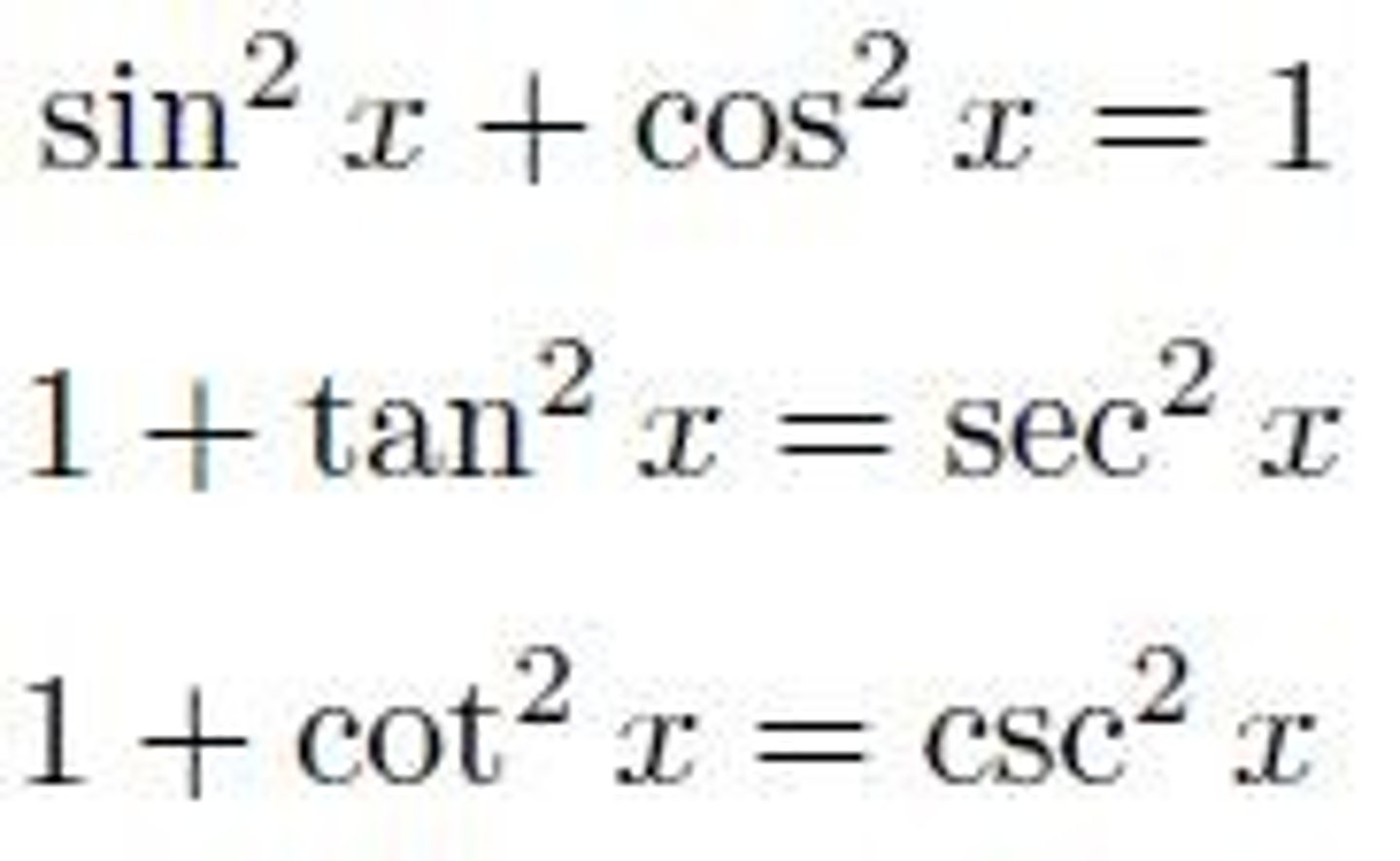
dy/dx

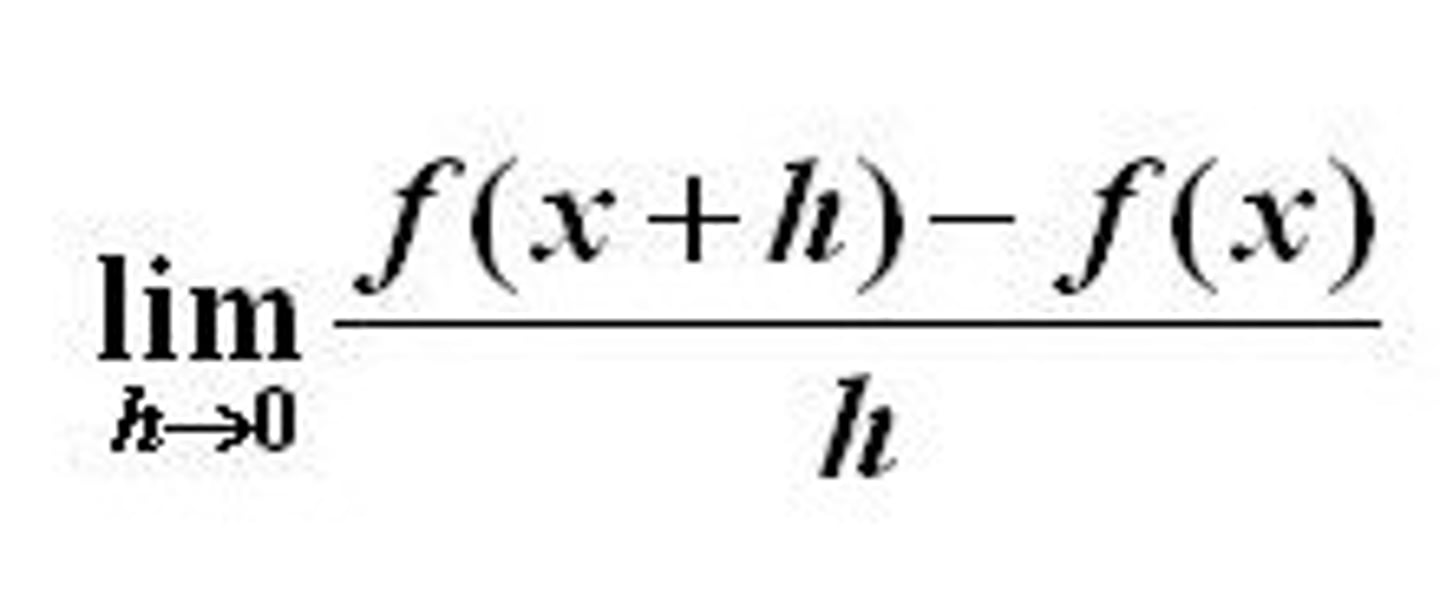
Intermediate Value Theorem

Extreme Value Theorem

There must be a max and min if the function is continuous on [a,b]

Linear Approximation

F(x)~=~f(a) +f`(a)(x-a)

Finding Average Velocity

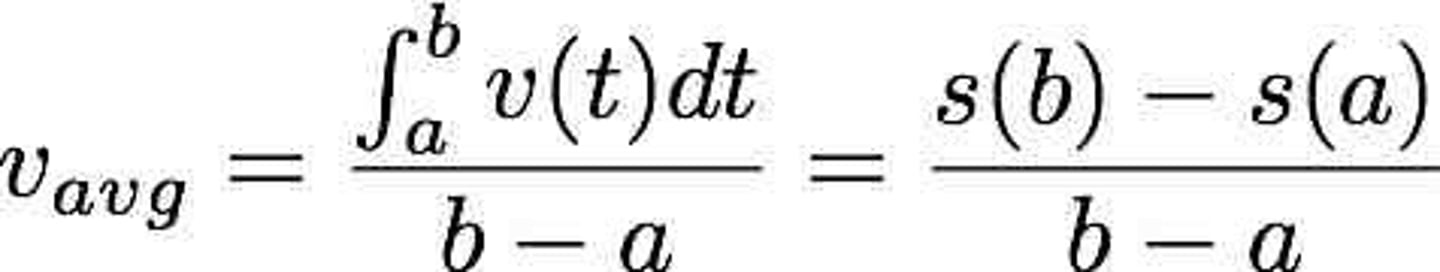
Numerical Differentiation

Used to estimate the derivative

(F(x+h)-f(x))/h

Inflection Points

To find inflection points

1. Find the second derivative

2. Set the second derivative equal to zero

3. Solve for x

Optional

4. Plug in and solve for f(x)

Mean Value Theorem

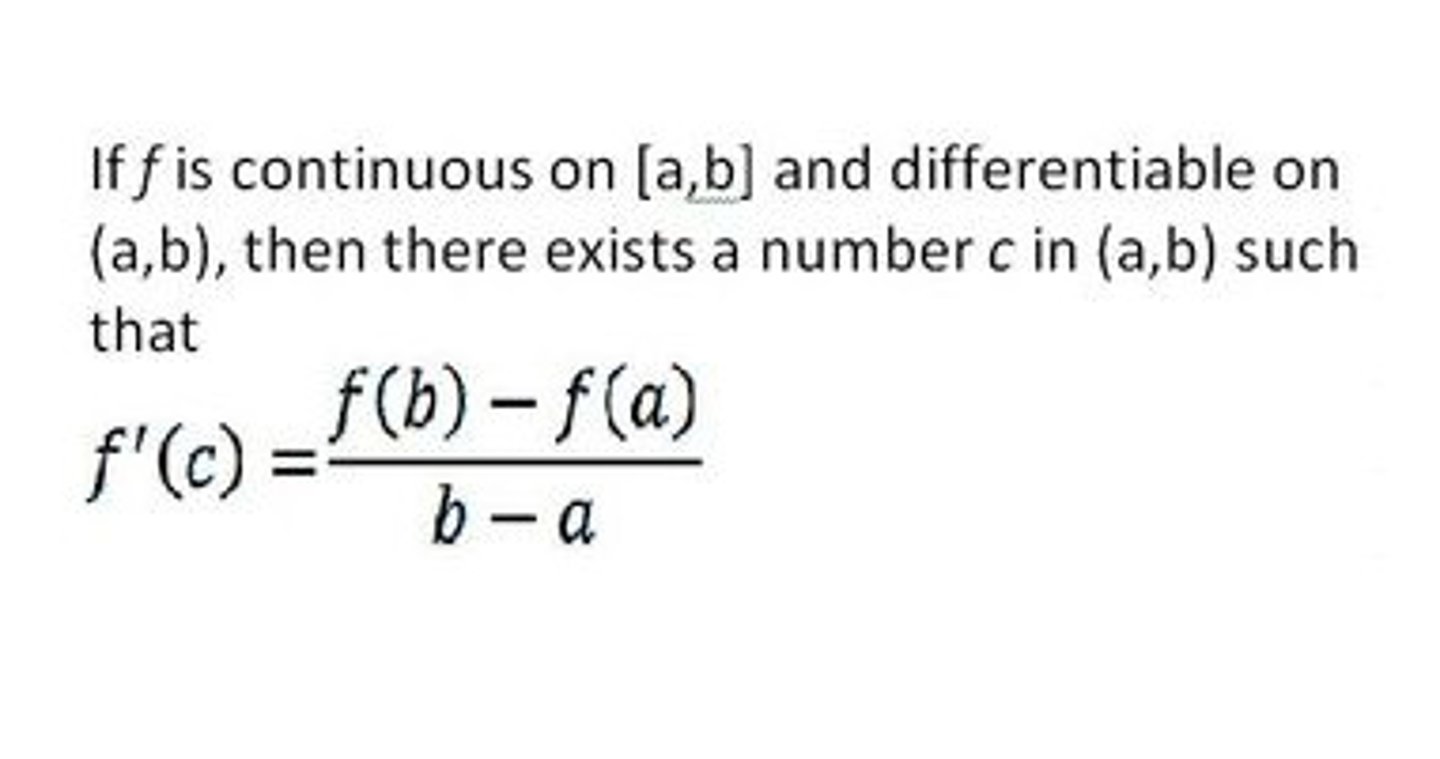
F(x): Increasing or Decreasing

If f`is positive, then f(x) is increasing

If f` is negative, then f(x) is decreasing

F(x): Concavity

If f`` is positive, then f` is increasing, and the concavity of f(x) is upwards

If f`` is negative, then f` is decreasing, and the concavity of f(x) is downwards

Absolute Max./Min.

Only occur at critical points or end points of a continuous function (guaranteed by the EVT)

Differentiation: Product Rule

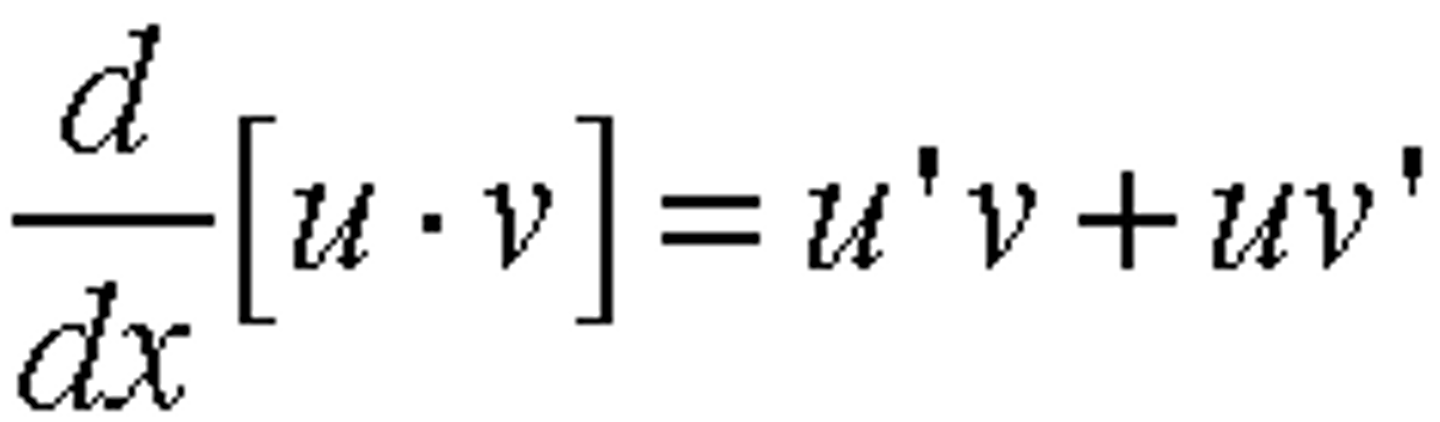
Differentiation: Quotient Rule

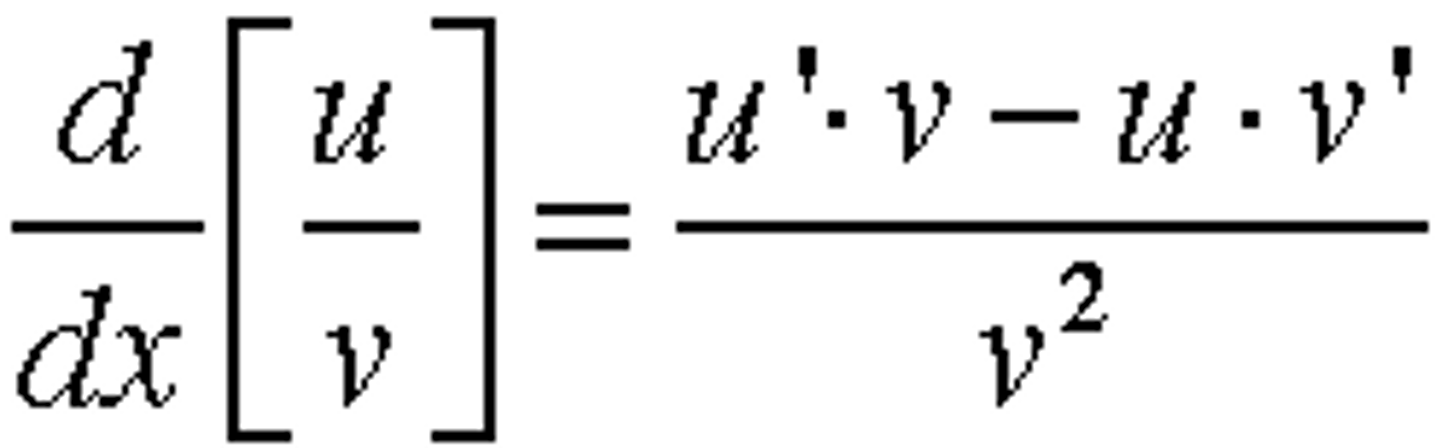
Differentiation: Chain Rule

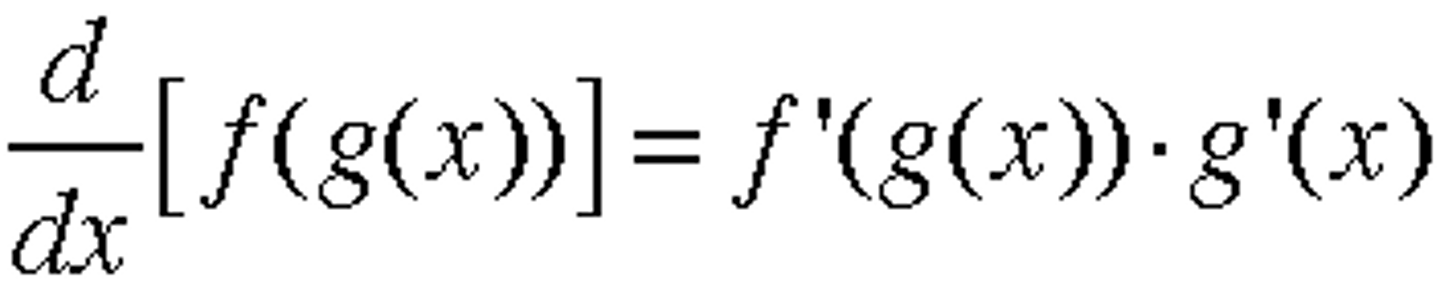
Differentiation: Inverse Functions

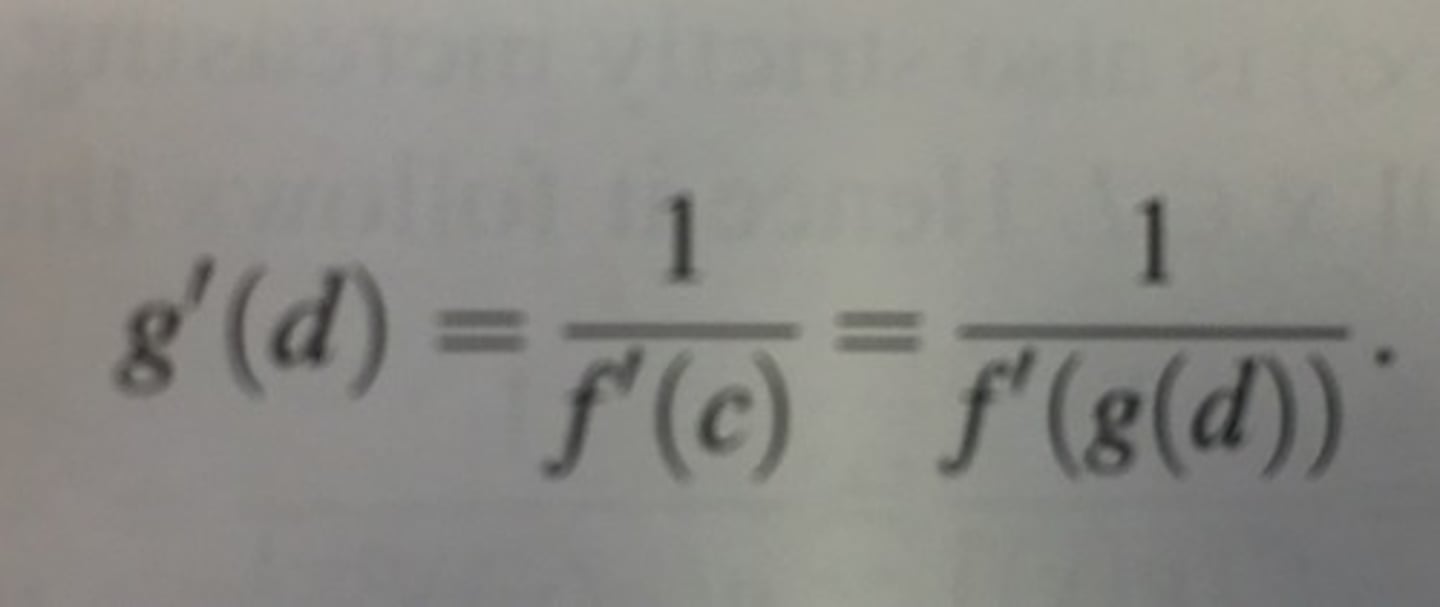
Differentiation: Implicit Functions

Differentiation: Power Rule

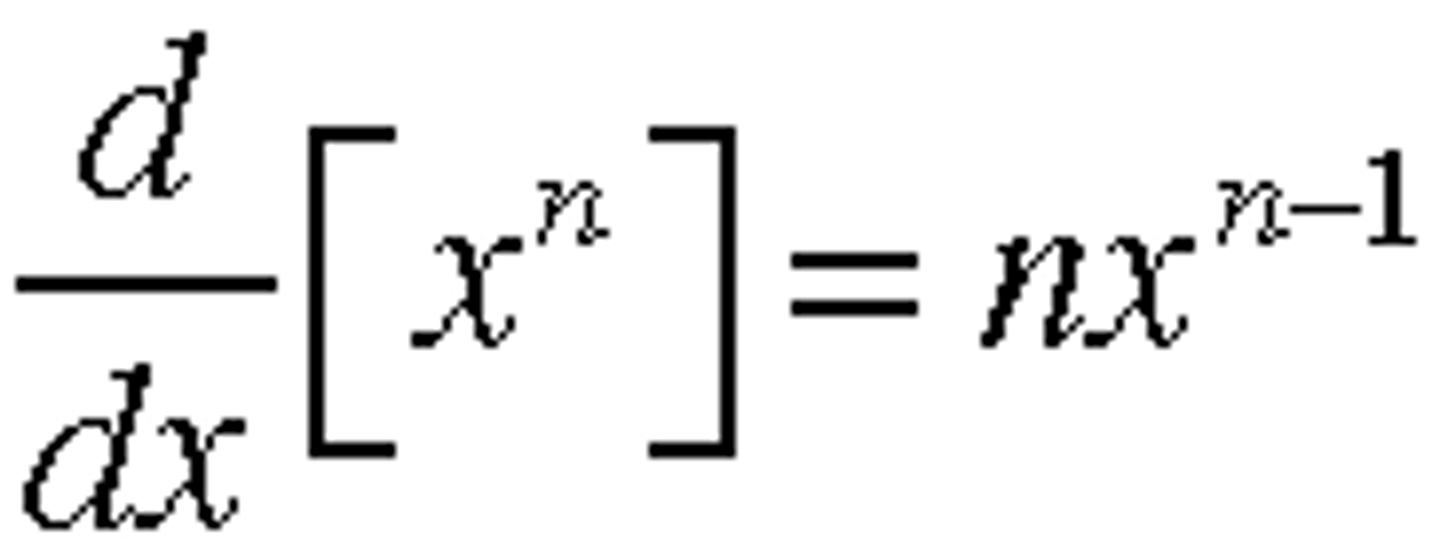
Differentiation: Logarithms

d/dx of ln|x| = 1/x

d/dx of log base a of |x| = 1/(ln(a)x)

d/dx of ln|f(x)| = f`(x)/f(x)

Differentiation: Trig Functions

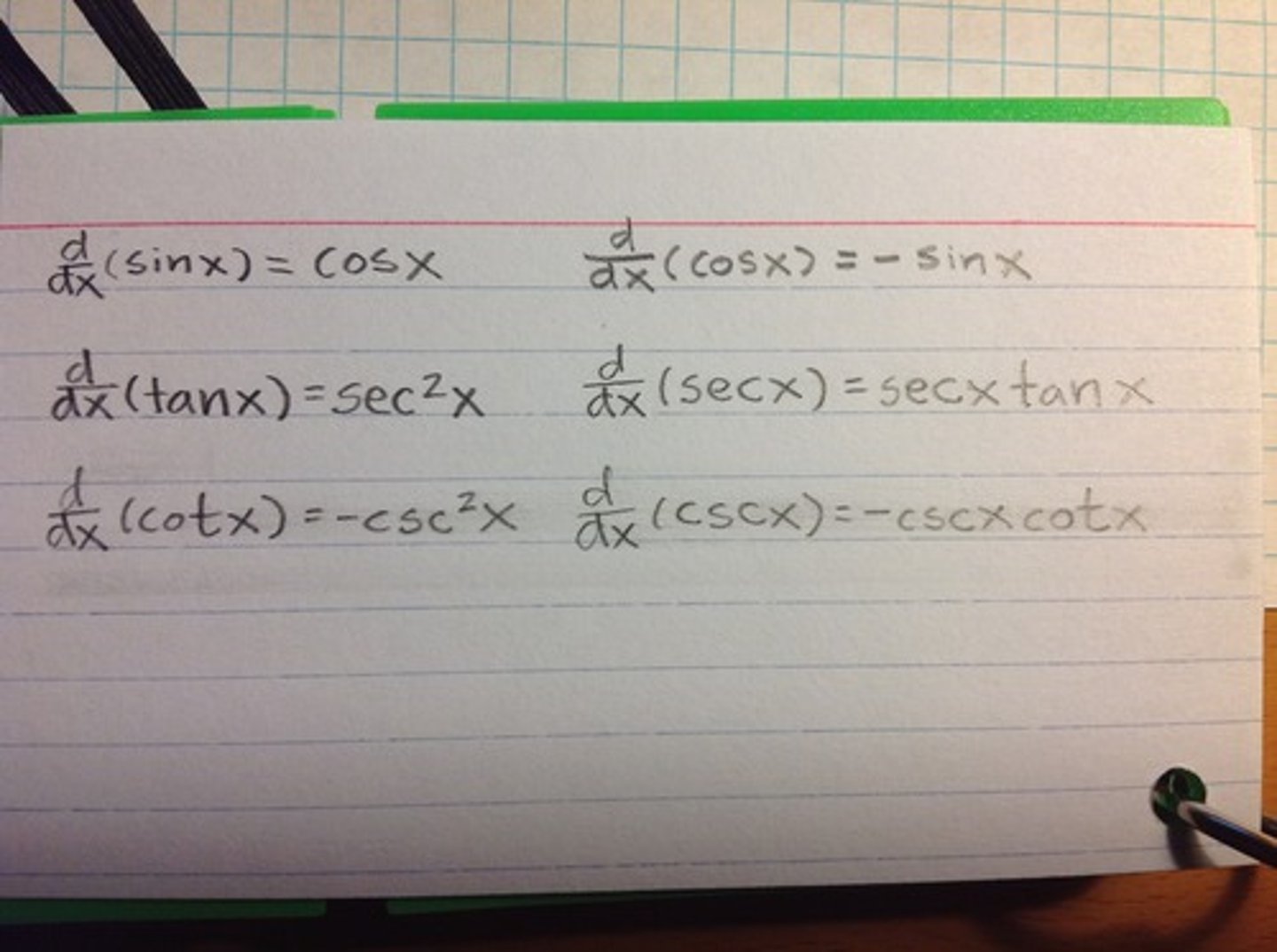
Related Rates

Suppose two variables, each a function of "time", are related by an equation.

1. Differentiate both sides of the equation

2. Use data given for variables and on of the rates to solve for the other rate

Optimization with Constraint

1. Visualize the problem; name the variables

2. Write down the objective function - the one to be optimized - as a function of two variables

3. Write down a Constraint Equation relating the variables

4. Use the constraint to rewrite the objective function in terms of one variable (Isolate one of the variables and then plug in for that variable)

5. Analyze the new function of one variable to find its optimal point(s) and the optimal value

Indefinite Integral

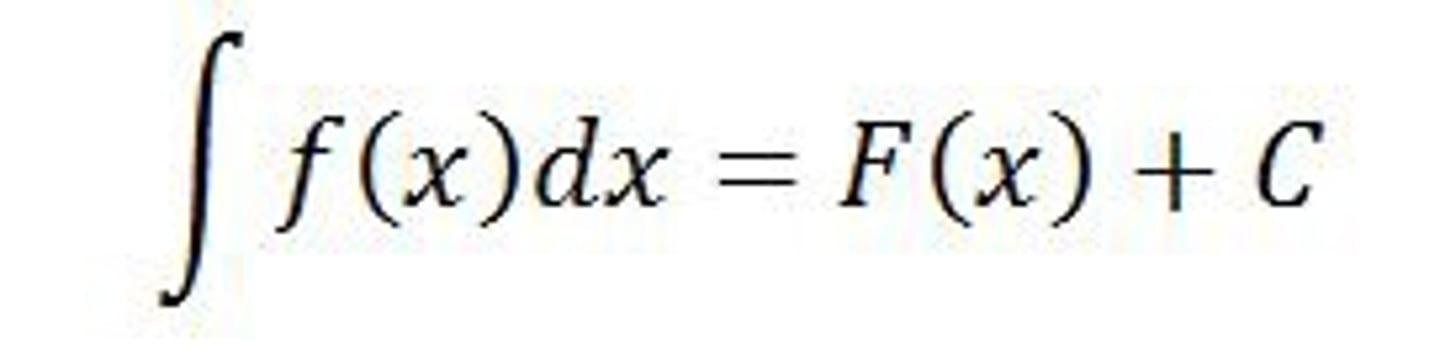
Definite Integral

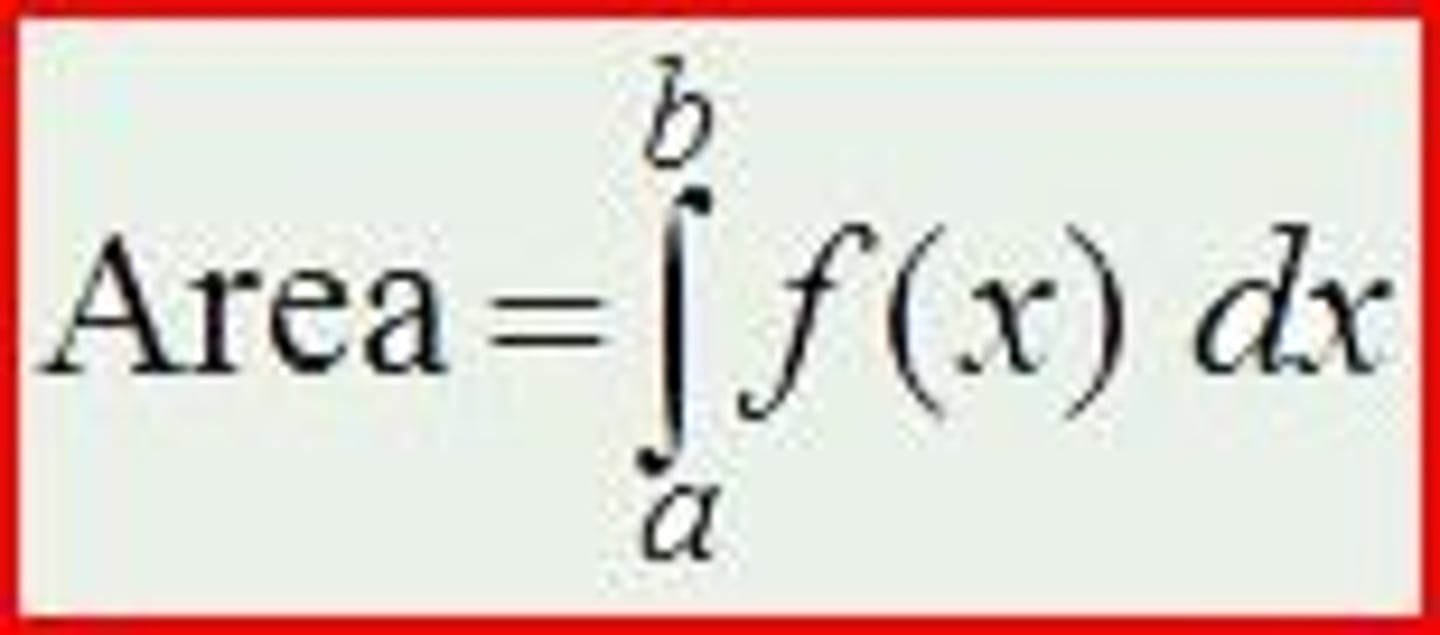
Fundamental Theorem of Calculus

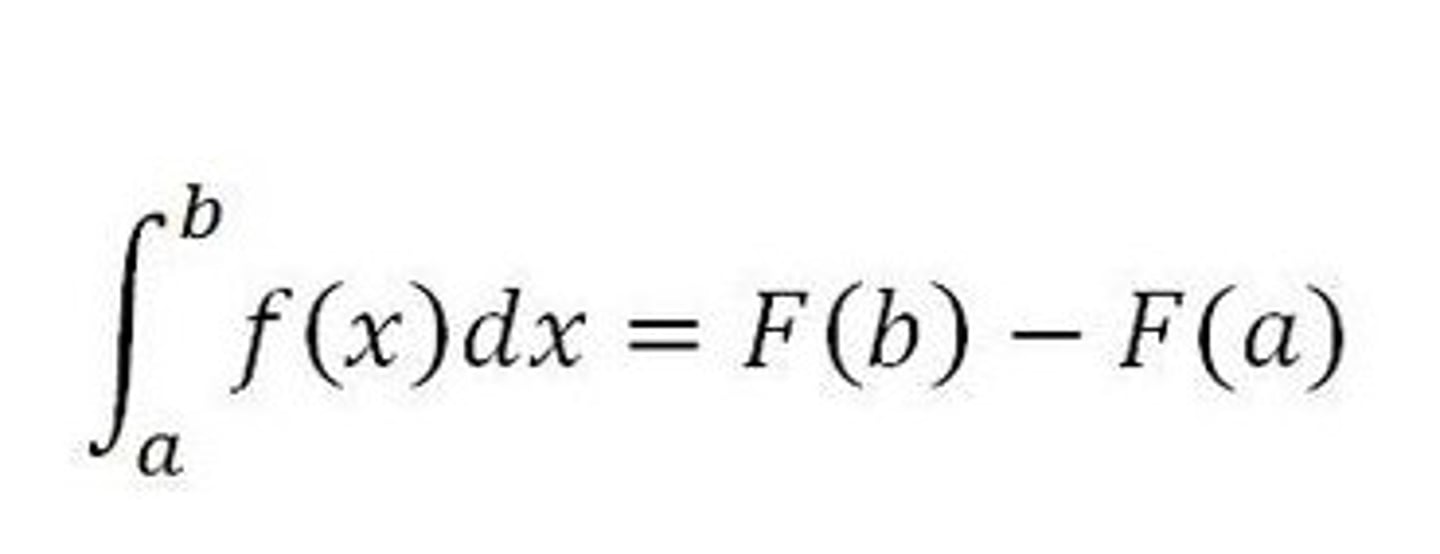
Second Fundamental Theorem of Calculus

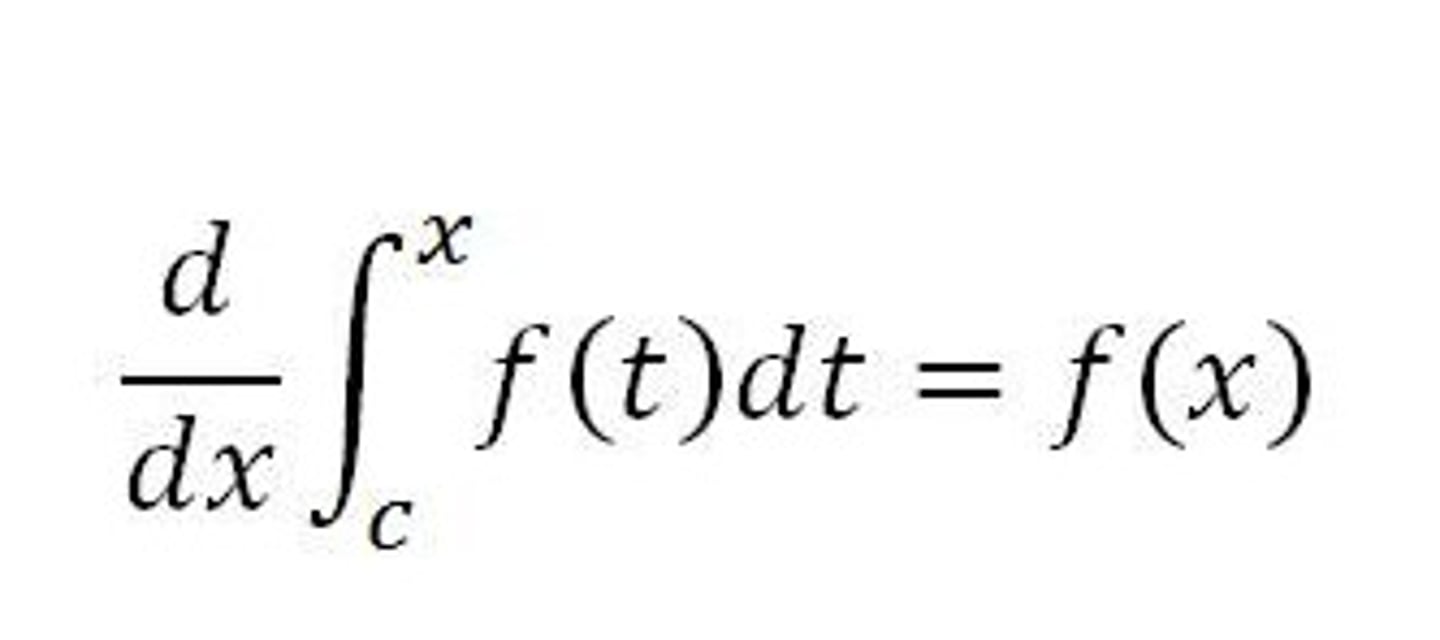
MVT for Integrals

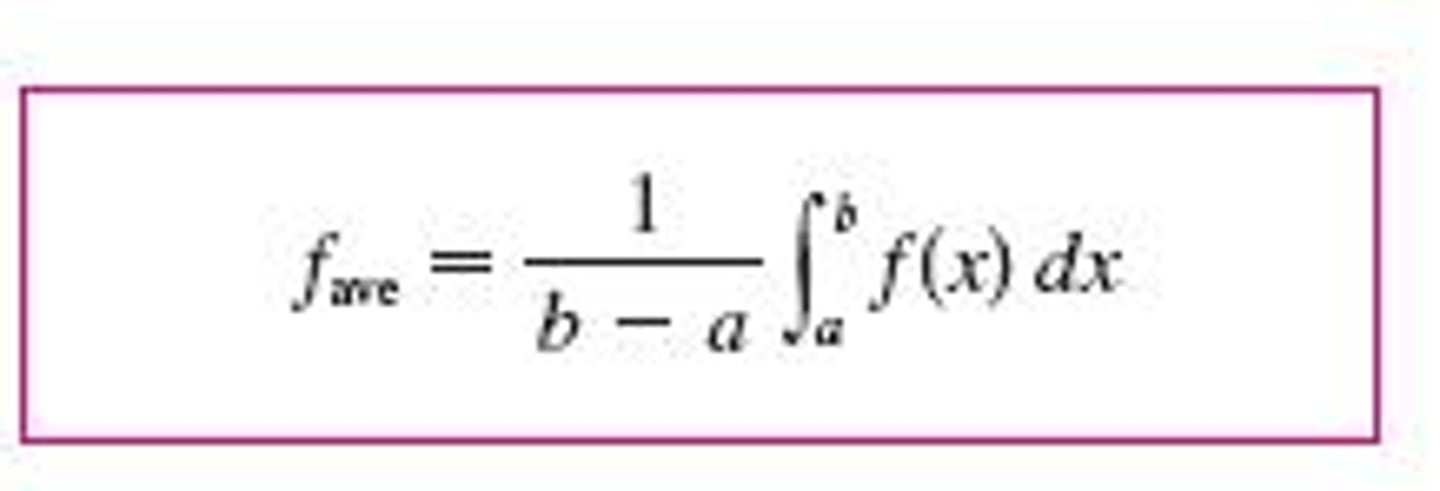
Integration: Power Rule

Integration: Natural Logarithm

(squiggly line antiderivative)d/du = ln|u| + C

Integration: Exponential Function

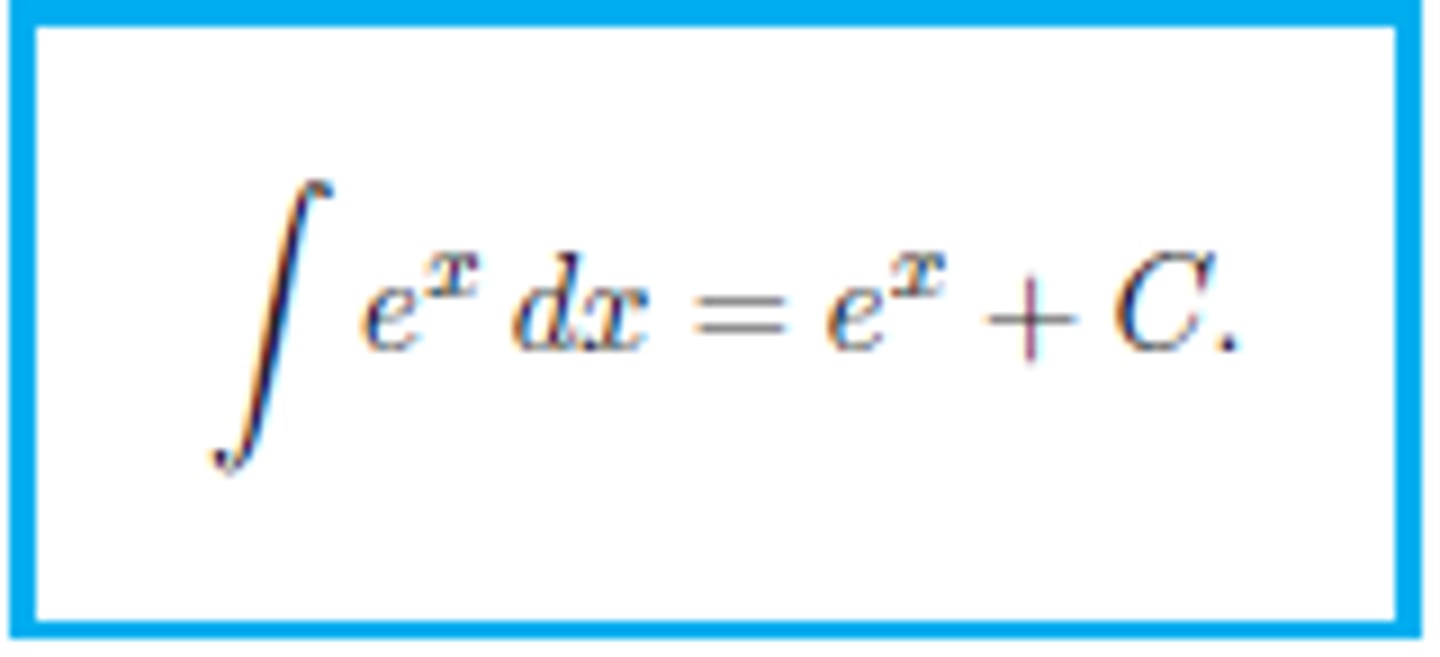
Integration: Trig Functions

http://calculus.nipissingu.ca/tutorials/integralgifs/int_indef_trigtable.gif

Area Between Curves

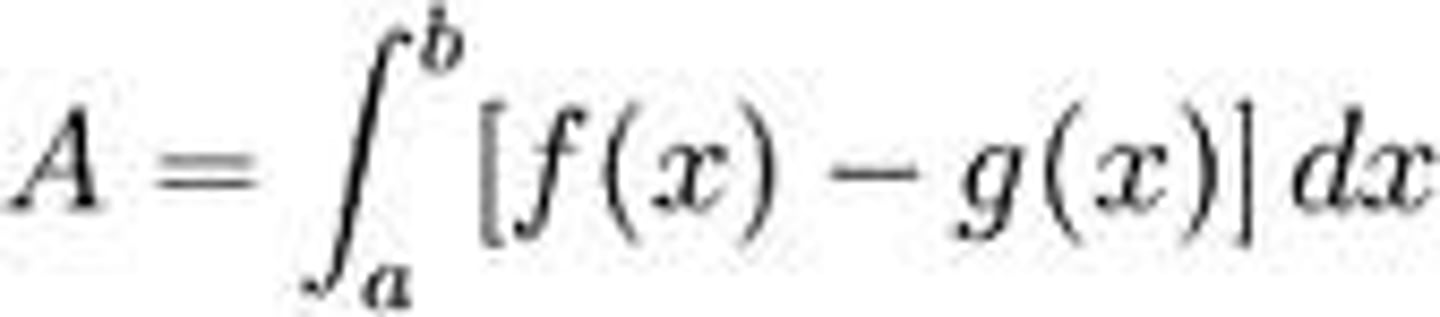
Volumes of Solids of Revolution

Rotating the the region between two curves about a line, then finding the volume created

Disk Volume

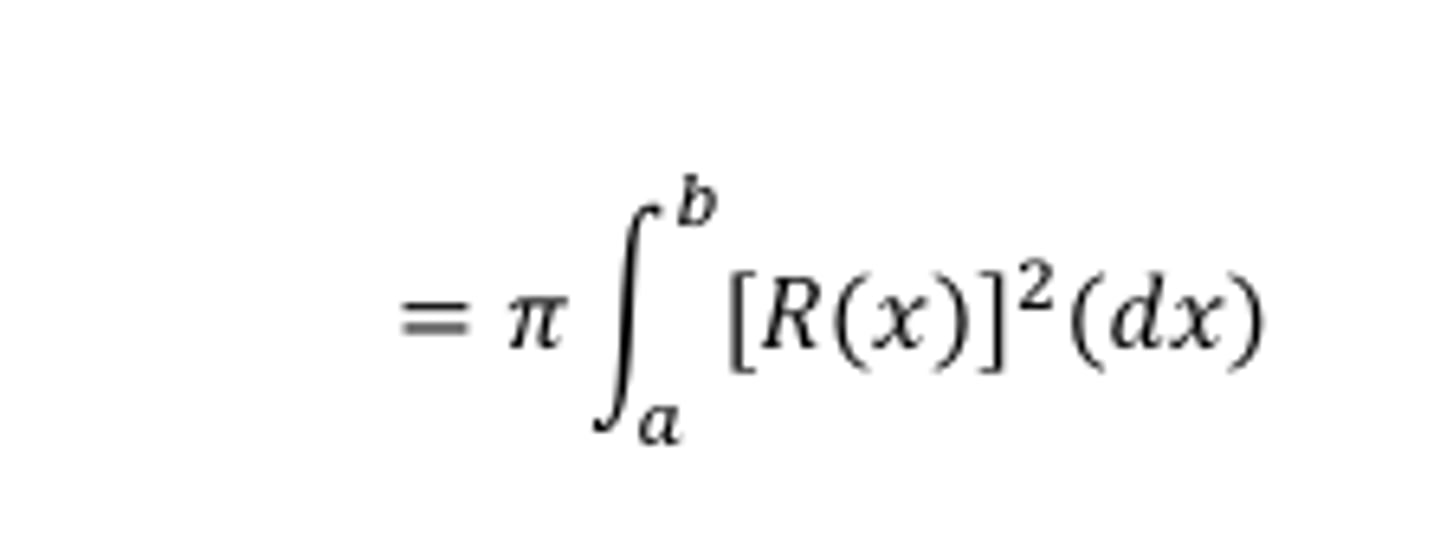
Washer Volume along x axis

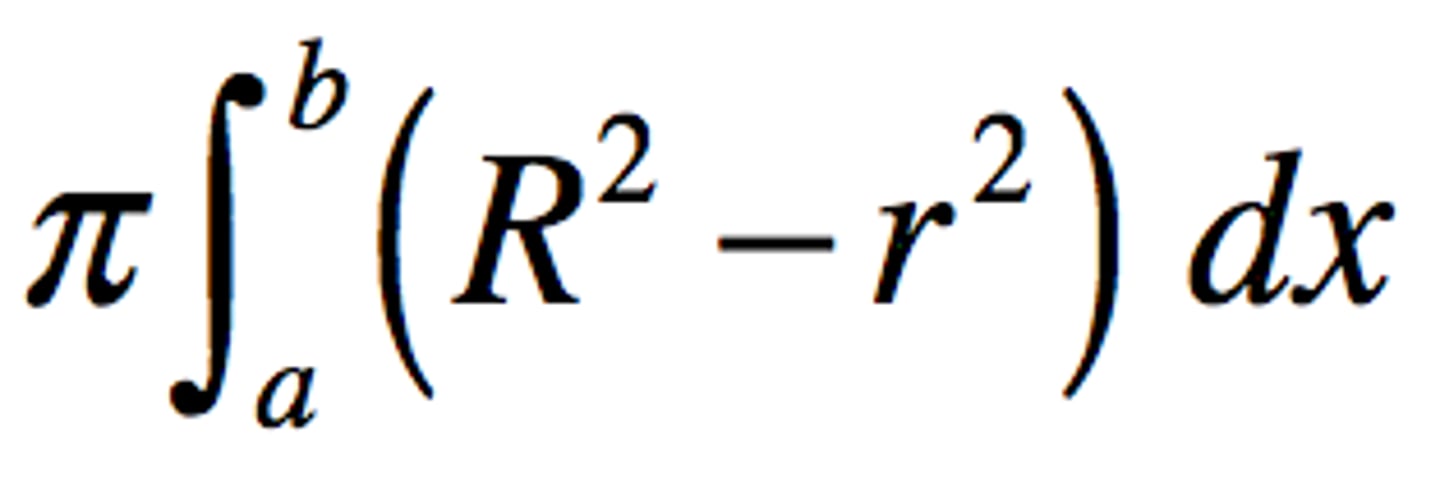
Washer Volume along y axis

Same as along the x axis simply replace x with y (replace every single x with a y)

Cylindrical Shell Volume

h = R-r

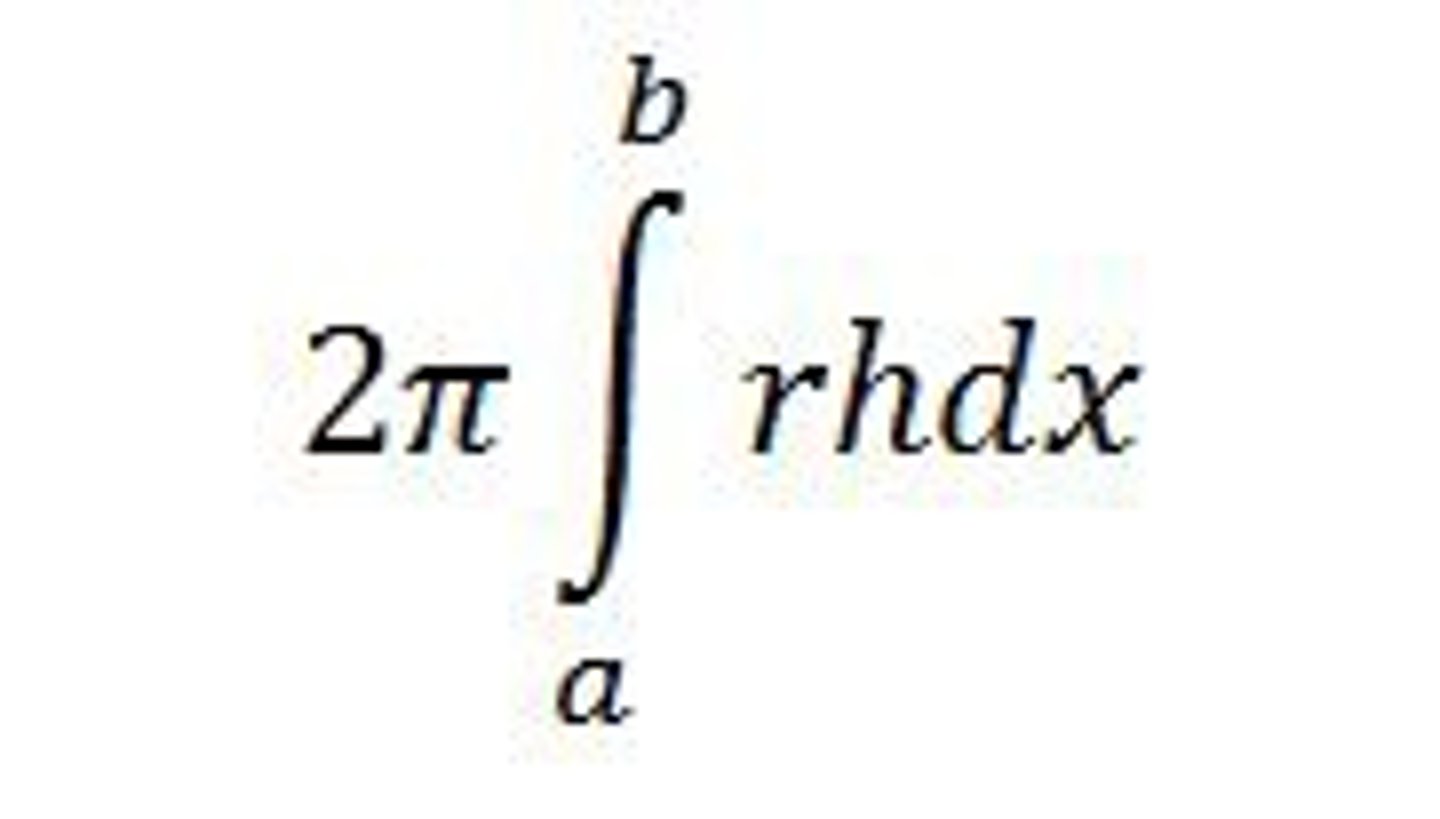
Riemann Sum

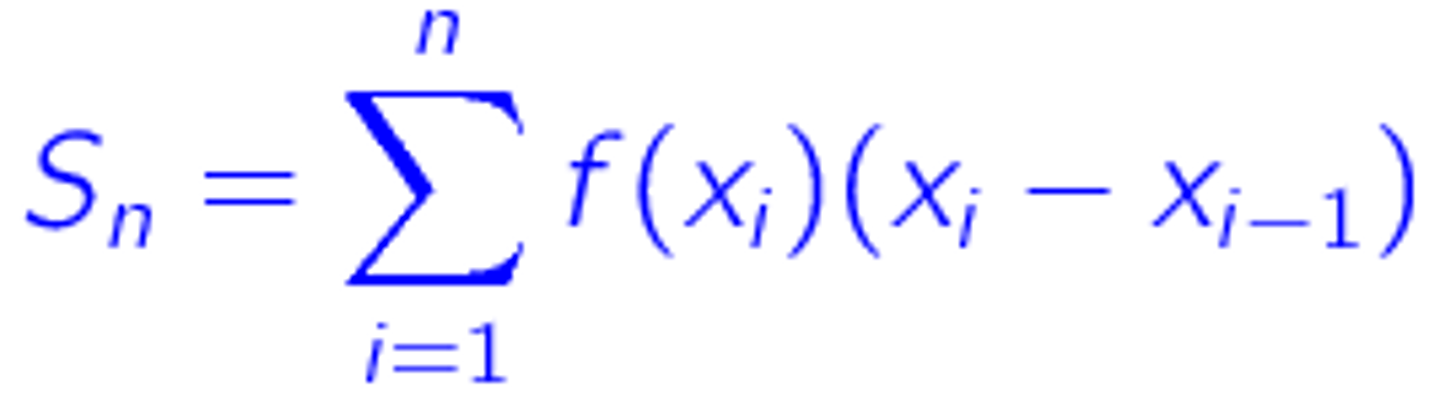
Riemann Sum: Trapazoidal

http://images.slideplayer.com/22/6418662/slides/slide_4.jpg