Wiskunde ex 2

Eenheidsvectoren

E_x, E_y en E_z

co(A^→B)=? als co(A^→)=(x₁,y₁) en co(B^→)=(x₂,y₂)

(x₂-x₁,y₂-y₁)

norm van een vector (definitie)

de lengte van de vector

norm van een vector (formule)

uitz. (bij 2D-vlak z-waarden weglaten)

‖A^→B‖=|AB|=√((x₂-x₁)²+(y₂-y₁)²+(z₂-z₁))

norm van een puntvector (bij puntvector 2D enkel 2 variabelen)

‖P^→‖=|OP|=√(x²+y²+z²)

formule van Chasles-Möbius

A^→B+B^→C=A^→C

zwaartepunt (definitie)

Het snijpunt van de zwaartelijnen van een driehoek.

zwaartelijn (=lijn van hoek tot midden van overstaande zijde)

zwaartepunt Z^→(formule)

(bij een driehoek en vierhoek)

Z^→=(A^→+B^→+C^→)/3 (bij driehoek)

Z^→=(A^→+B^→+C^→+D^→)/4 (bij vierhoek)

midden van een lijsntuk (formule)

M^→=(A^→+B^→)/2

richtingsvector (definitie)

een vector U^→ die de richting bepaald van de rechte a dat verschillend is van de nulvector

U^→(l,m,n)

richtingsrechte (definitie)

de rechte door de oorprong en evenwijdig met de rechte a

vectoriële vergelijking van de rechte a

a↔

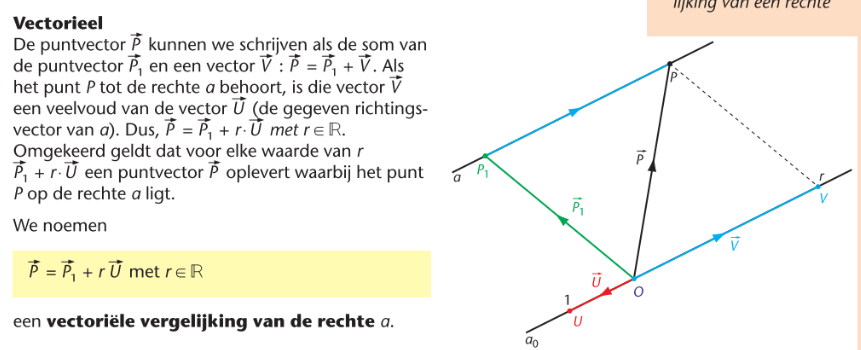
de stelsel parametervergeljkingen van de rechte a

a↔

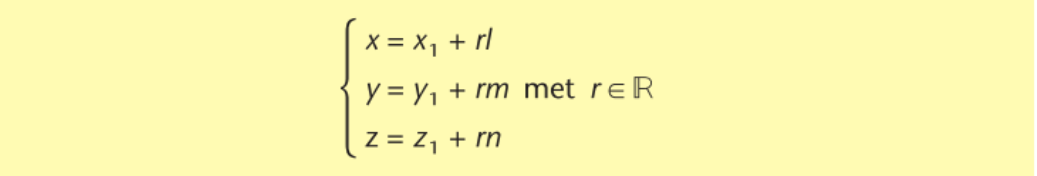
de stelsel cartesiaanse vergelijkingen van de rechte a (3 manieren/notaties)

a↔

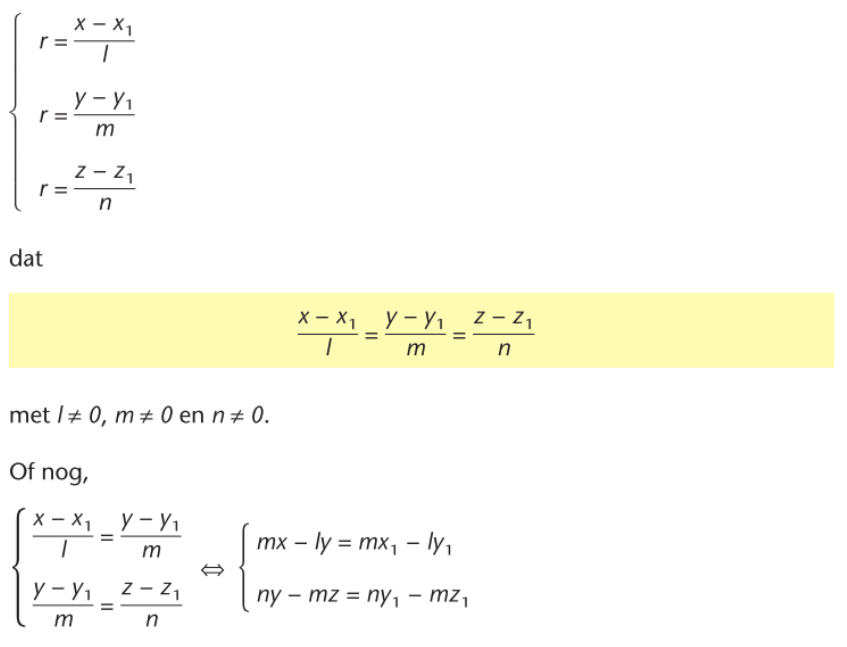
stelsel cartesiaanse vergelijkingen richtingsrechte a₀ (de rechte evenwijdig met rechte a en door de oorsprong)

a₀↔

(Homogene stelsel van a)

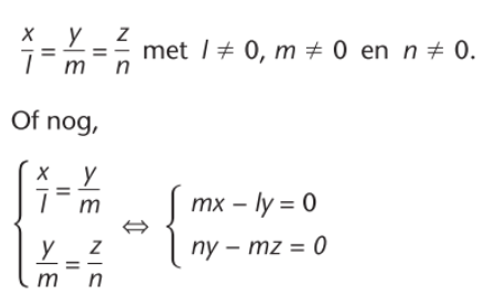
samenvatting onderlinge ligging

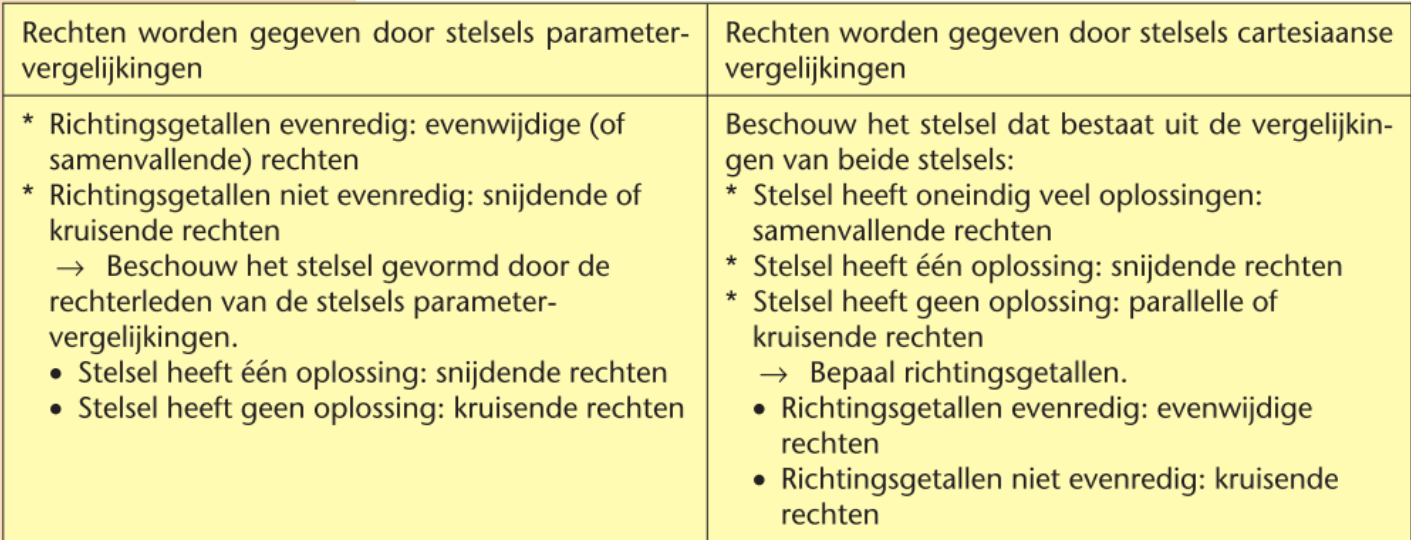
hoek tussen twee rechten (definitie)

is de kleinste positieve hoek tussen hun richtingsrechten

scalair product van 2 vectoren (formule)

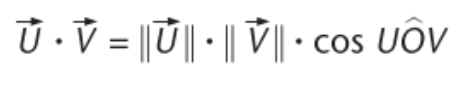
hoek tussen 2 vectoren (formule)

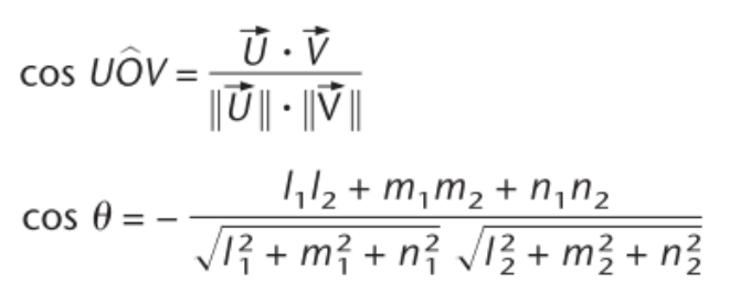
loodrechte stand van 2 vectoren

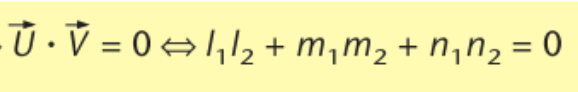
vectoriërle vergelijking van het richtingsvlakvlak α₀ door O, U en V

een stelsel parametervergelijkingen van het richtingsvlak α₀ door O, U(l₁,m₁,n₁) en V(l₂,m₂,n₂)

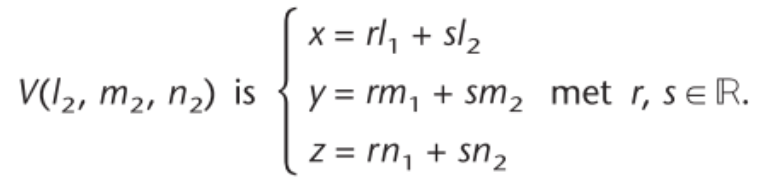
stel richtingsgetallen van α

de coördinaatgetallen van een richtingsvector van het vlak α

stel richtingsvectoren van α

de twee richtingsvectoren van het vlak α die geen veelvouden zijn van elkaar

richtingsvlak α₀ (def)

is een vlak door de oorsprong dat evenwijdig is met het vlak α

vectoriële vergelijking van het vlak door A met een stel richtingsvectoren(=de 2 richtingsvectoren) U^→ en V^→)

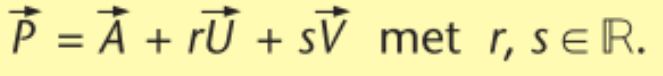
cartesiaanse vergelijking van het richtingsvlak α₀ door O

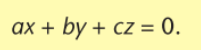
stelsel parametervergelijkingen van het vlak door A(x₀,y₀,z₀) met richtingsvectoren U^→ en V^→

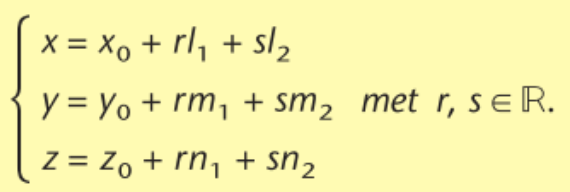
cartesiaanse vergelijking van een vlak α

ax+by+cz=d

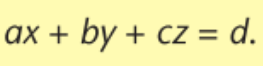
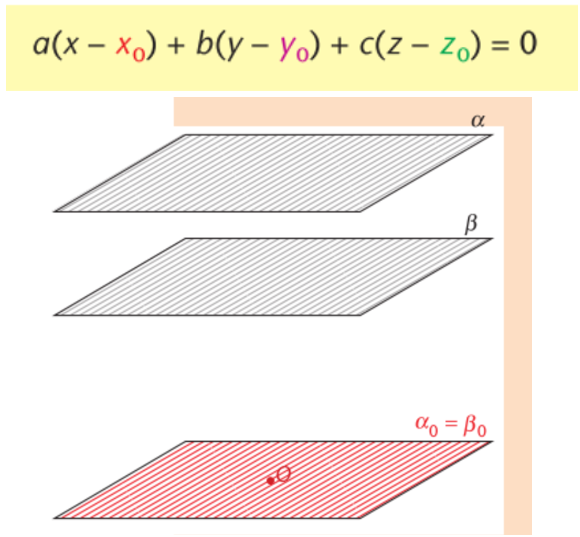
Wat is de cartesiaanse vergelijking van het vlak β door A en evenwijdig met α als α↔ax+bx+cz=d en A(x₀,y₀,z₀)

(evenwijdige vlakken hebben evenredige richtingsvlakken)

onderlinge ligging van een vlak en een rechte

• Een rechte en een vlak zijn snijdend of evenwijdig

• Vlakken en rechten die elkaar snijden, hebben één punt gemeen: het snijpunt

• als een rechte en een valk evenwijdig zijn, ligt de rechte al dan niet in het vlak.

onderlinge ligging tussen 2 vlakken en van een rechte en een vlak berekenen

zie p. 65-70

onderlinge ligging tusen twee vlakken

• twee vlakken zijn snijdend of evenwijdig

• snijdende vlakken snijden elkaar volgens een rechte: de snijlijn

• evenwijdige vlakken zijn al dan niet samenvallend

samenvatting onderlinge ligging

Normaalvector (definitie)

is een vector van een vlak (verschillend van de nulvector) die loodrecht staat op dat vlak

eigenschap normaalvector (cart. vgl.)

als ax+by+cz=d een cartesiaanse vergelijking is van een vlak α, dan is N^→(a,b,c) een normaalvector van α

hoek tussen 2 snijdende vlakken α en β (definitie)

is de hoek tussen de respectieve snijlijnen met de loodvlak γ op de snijlijn van α en β

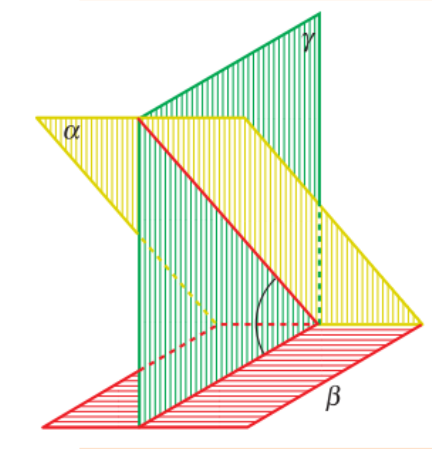
eigenschap bij hoek tussen 2 vlakken

de hoek tussen 2 vlakken is gelijk aan de de hoek van respectieve loodlijnen op deze vlakken

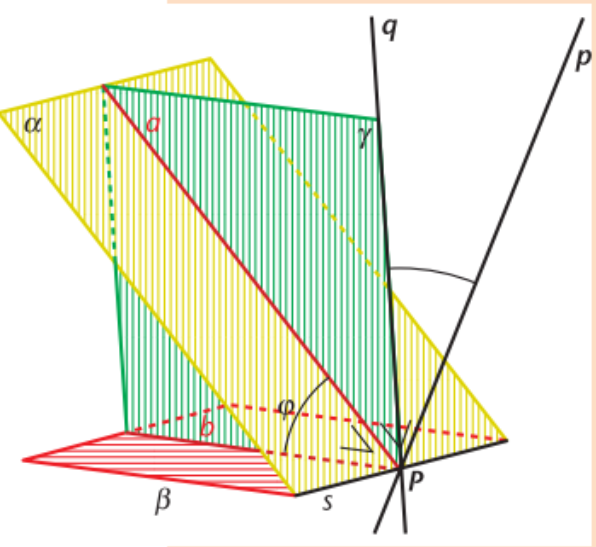
definitie vlakken die loodrecht staan op elkaar

als de normaalvectoren loodrecht staan op elkaar

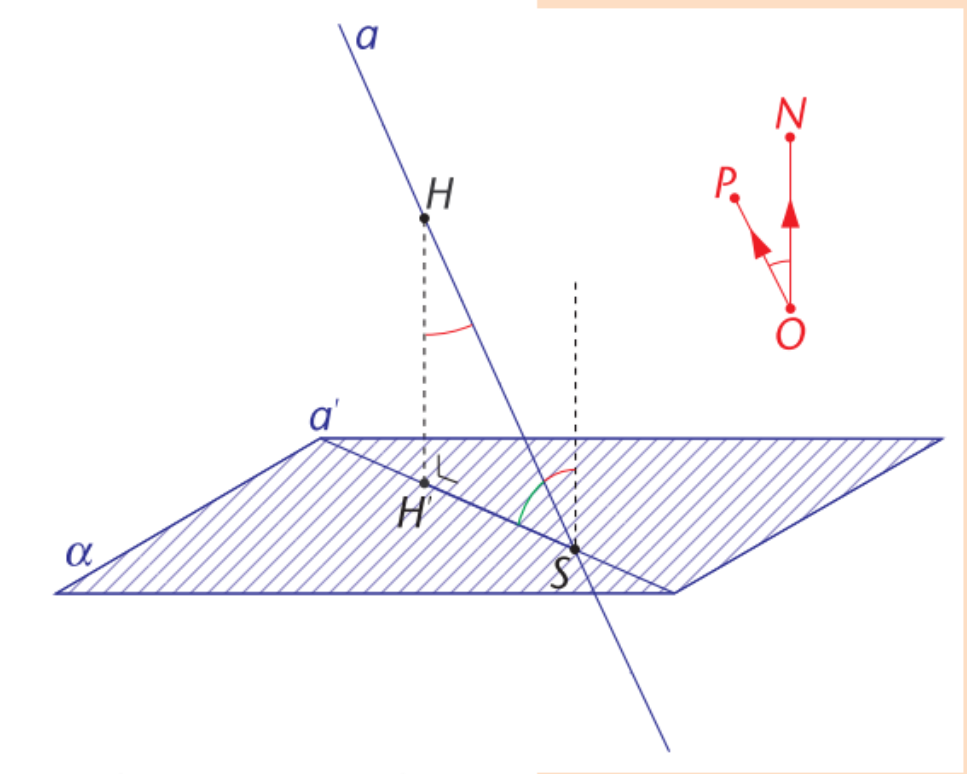
hoek tussen een vlak α en een rechte a (dat niet loodrecht staat op α) (definitie)

is de hoek tussen de rechte a en de loodrechte projectie a’ van de rechte a op het vlak α (=normaalvector op snijpunt tussen vlak en rechte)

LET OP!: is de groene hoek Ψ = 90°- φ
rode hoek: cos φ =… (zie p75)

opstellen van pm vgl en cart vgl

zie p. 60

Vlakkenwaaier (definitie)

verzameling van alle vlakken die eenzelfde rechte(=snijlijn) gemeenschappelijk hebben

middelloodvlak van een lijnstuk [AB] (definitie)

vlak loodrecht op de rechte AB en door het midden van [AB]

(= verzameling van alle punten op gelijke afstand van A en B)

afstand tussen vlak en punt (formule)

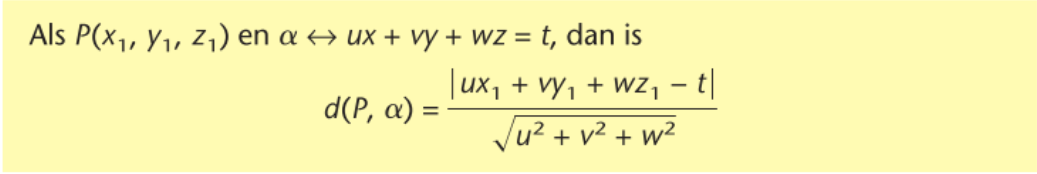
afstand punt tot een rechte

zie p. 86-87

afstand tussen twee kruisende rechten

zie p. 88-90

gemeenschappelijke loodlijn (definitie)

Is de gemeenschappelijke rechte van twee kruisende rechten die loodrecht staan op elkaar en de kortste weg is tussen de twee rechten.

gemeenschappelijk loodlijnstuk van kruisende rechten a en b

Is de lijnstuk dat begrensd is door de respectieve snijpunten P en Q van de rechten a en b met het loodvlak l.

(= tussen de rechtren a en b) d(a,b)=|PQ|

afstand van punten op gelijke afstand van twee evenwijdige, niet-samenvallende vlakken (formule)

γ ↔ ux+vy+wz= (t₁+t₂)/2

middenparellelvlak

Zijn alle punten die op gelijke afstand zijn van evenwijdige, niet-samenvallende vlakken.

punten op gelijke afstand van twee snijdende vlakken (formule)

(principe bissectrices van 2 snijdende rechten = rechte door stompe hoek en door scherpe hoek)

vlak van punten op gelijke afstand van twee snijdende vlakken (definitie)

deelvlakken of bissectorvlakken

snijlijn van vlakkenwaaier (formule)

r.α+s.β= vgl van alle vlakken met de snijlijn l

(dus deze formule is niet voor de snijlijn)