EGN 3365 Exam 2

The given stress-strain graph represents?

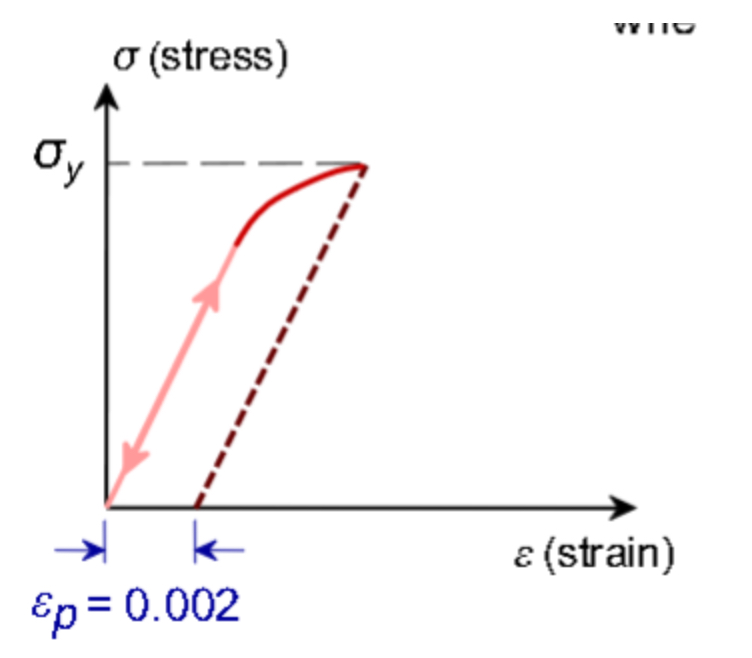
The given stress-strain graph represents?

Elastic then plastic deformation

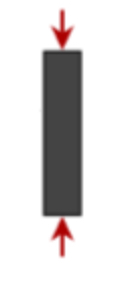
What does the figure represent?

Simple compression

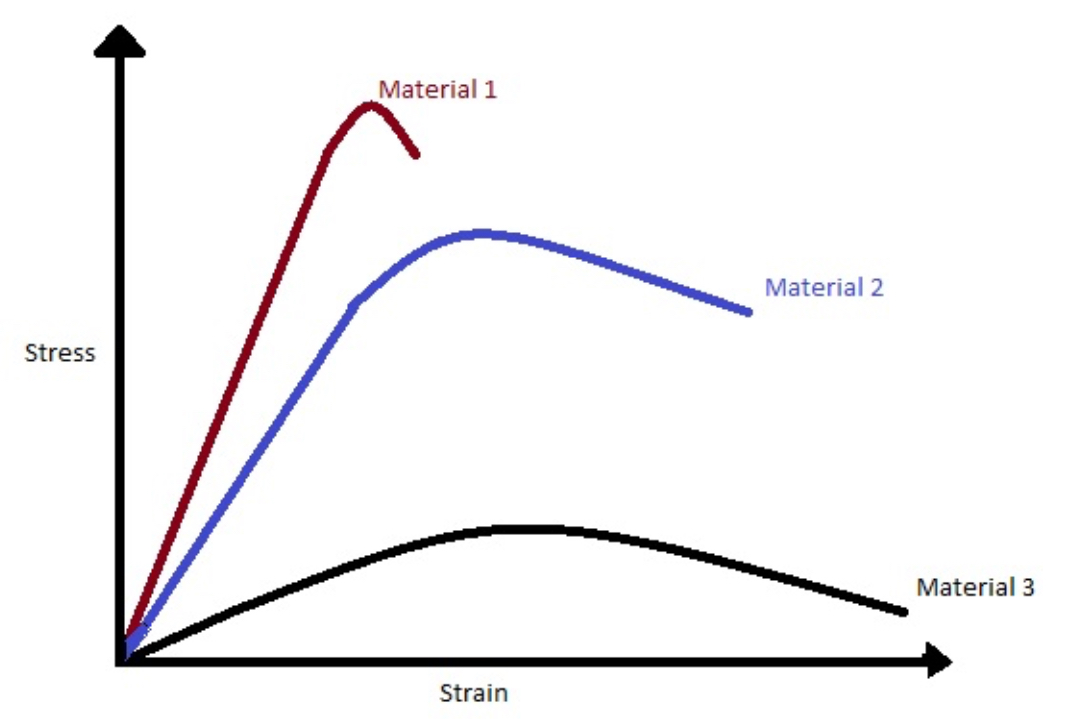
Which material has the highest toughness?

Material 2

For an engineering strain of 1, calculate percentage elongation (ductility) of the specimen?

100

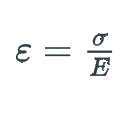
A specimen of copper having a rectangular cross-section 15.2 mm X 19.1 mm  is pulled in tension with 44,500 N  force, producing only elastic deformation. Calculate the resulting strain. ( Elastic modulus of copper = 110 GPa)

1.39 x 10^-3

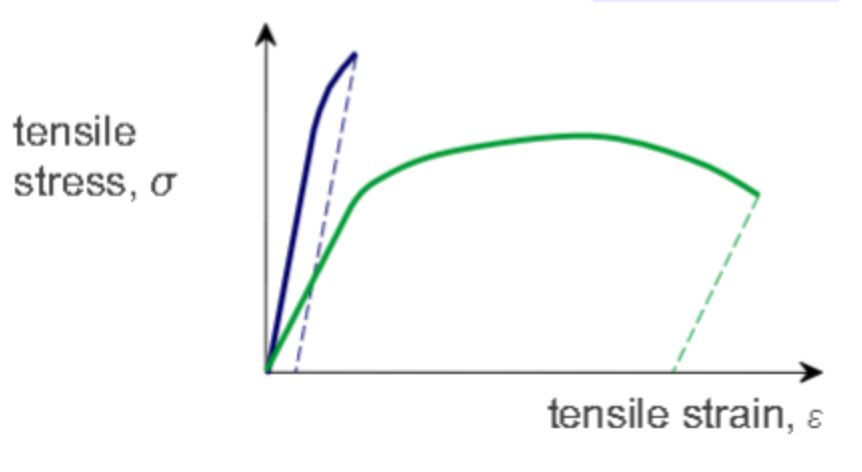
Ductility is the amount of plastic deformation at failure.

From the given graph below, determine which line represent a material with high ductility and which line represent a material with low ductility.

Blue line: Low ductility.

Green line: High ductility.

For some metal alloy, the true stress of 345 MPa produces a plastic true strain of 0.02. How much does a specimen of this material elongate when true stress of 415 MPa is applied if the original length is 500 mm? Assume a value of 0.22 for the strain-hardening exponent, n.

23.7mm

Poisson's ratio for metals, ceramics and polymers is in the range:

0.15 < v <= 0.5

Deformation of a sample to an engineering strain of 2 means that the sample is ___________ its original length.

A. Half

B. Twice

C. Three times

D. 2% longer than

Three times

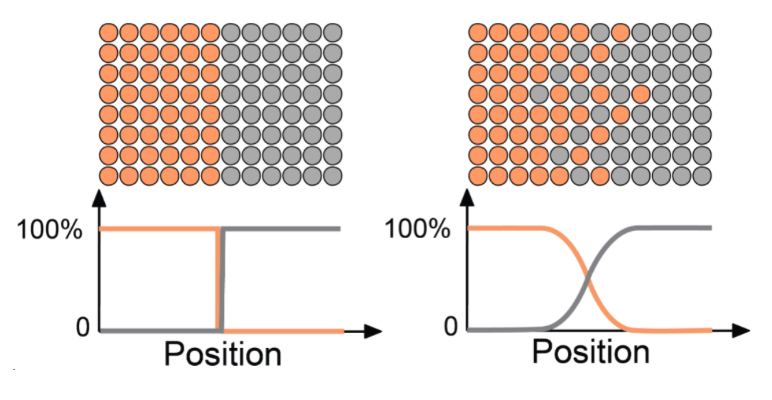
What best describes the figure?

A. Not an example of diffusion

B. Left: before diffusion, right: after diffusion

C. Left: after diffusion, right: before diffusion

D. None of the above

Left: before diffusion; right: after diffusion

What is diffusion

Mass transport by atomic motion

Atoms tend to _____________ from regions of _____________ concentration to regions of _____________ concentration.

Migrate, high, low

What is self-diffusion?

Migration of host atoms in pure metals

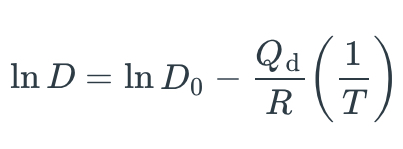
What is the derivation of the equation relating the diffusion coefficients at two temperatures T1 and T2, given that:

D₂ = D₁exp [-Qd/R(1/T2-1/T2)]

At 300°C the diffusion coefficient and activation energy for Cu in Si are

D₁ (300°C) = 7.8 × 10⁻⁻¹¹ m²/s

Qd = 41.5 kJ/mol

Compute the diffusion coefficient D₂ at 400°C.

28.46 × 10⁻⁻¹¹ m²/s

Non-steady state diffusion is a function of:

Time and position

Fick’s first law of diffusion is applicable to

Steady state diffusion

What’s Fick’s second law of diffusion?

dC/dt = D d²C/dx²

What's Fick’s first law of diffusion?

J = −D dC/dx

What’s the relationship between the diffusion coefficient and temperature?

Increases with increasing temp

What is interdiffusion?

Diffusion of atoms of one material into another material

Diffusion rate of vacancy diffusion depends on

Number of vacancies, activation energy

interstitial diffusion

smaller atoms diffuse between adjacent atoms, faster than vacancy diffusion

Case hardening is an example of _________ diffusion

Interstitial

case hardening

outer surface is hardened by diffusing carbon atoms into surface

Doping

adding impurities to a semiconductor to increase conductivity

Process of doping

1. P rich layers on surface

2. Heat it

3. Doped semiconductor regions

Diffusion is faster for

open crystal structures, materials with secondary bonding, smaller diffusing atoms, lower density materials

Tensile load (pulling)

If a specimen is being elongated or extended

Compressive load (pushing)

Specimen is compressed or contracted

Deformation

Change in dimension

shear forces

Parallel to cross sectional area

Plastic deformation

permanent change in shape by bending and folding

Elastic deformation

material returns to original state when stress is removed

Common states of stress

Simple tension, torsion, simple compression, bi-axial tension, hydrostatic compression

Yield strength

point where the material begins to plastically deform

Toughness

the ability of a material to resist fracture

Hardness

resistance to localized surface deformation and compressive stresses

Resilience

Ability of a material to store energy

Ductility

amount of plastic deformation at failure

Engineering stress

tensile, shear

Engineering strain

tensile, lateral, shear

Percent elongation

the total percent increase in length of a specimen during the tensile test

Dislocation

A defect where atoms are misaligned around it

Edge dislocation

extra half plane of atoms inserted into a crystal structure

Dislocation line

The line where dislocations happen

Screw dislocation

lattice plane shifts similar to a spiral staircase

Burgers vector

measure of lattice distortion

Twin boundary

a reflection of atom positions across the twin plane

Solidification

Result of casting molten material

Grain boundaries

Regions between grains (crystals)

Point defects

vacancy, interstitial atoms, substitutional atoms

Vacancies are

vacant atomic sites

Dislocations move when

Stresses are applied

A catalyst ____________ the rate is a chemical reaction without being consumed

Increases

Dislocation types include

Edge, screw, and mixed

two diffusion mechanisms

vacancy and interstitial

The applied mechanical force is normalized to

Stress

The degree of deformation is normalized to

strain

Elastic deformation is

nonpermanent and reversible

Plastic deformation is

permanent and nonrecoverable

Stiffness

a material's resistance to elastic deformation

Strength

A materials resistance to plastic deformation

In an optical microscope, grain boundaries appear as white lines after the surface is prepared by etching. T/F

false

According for Fick’s first law, the concentration of diffusing species is a function of both time and position. T/F

false

D_interstitial << D_substitutional

T/F

false

In edge dislocation, burger’s vector is perpendicular to dislocation line. T/F

true

Diffusion coefficient _________ with increasing temperature

increases

What are the interfacial defects?

twin boundaries, grain boundaries, stacking faults

I can observe individual atoms using an optical microscope. T/F

false

What’s an example to processing using diffusion

case hardening

Interstitial diffusion is more rapid than vacancy diffusion. T/F

true

Equiaxed grains are

Roughly the same dimension in all directions

Columnar grains are

grains elongated in one direction

Rate of diffusion is __________ of time

independent

Diffusion is ____________ of time

dependent

What are the 5 interfacial defects?

external surfaces, phase boundaries, optical boundaries, twin boundaries, stacking faults