Introducción a la estadística

Fenómenos

Deterministas:

• No hay variabilidad

  • no se aplica estadística

Estocástico

• Con variabilidad

  • se aplica estadística

Cómo se dice a la información recogida?

Variable (s)

Qué es un individuo?

Elemento que forma parte de la población

Es lo que estudiamos

No tiene por qué ser humano, puede ser objeto u elemento

• Ejemplo:

  • Urgencia en hospital —> cada visita es un individuo y una persona puede tener varias visitas

Qué es la población?

Conjunto de todos los individuos o unidades que son objeto principal del estudio

La población puede ser:

• pequeña

• grande

• abstracta (lanzamientos de un dado)

Qué es la muestra?

Subconjunto de la población a la que accede el investigador para recoger la información deseada (la muestra debe ser representativa de la población)

Qué es la variable?

Característica de los individuos de interés para nuestra investigación que puede tomar diferentes valores

Variable independiente (VI):

• Método de toma de notas

  • Categorías: portátil / bolígrafo y papel.

Variable dependiente (VD):

• Rendimiento académico

  • Medido, por ejemplo, mediante la nota de un examen o prueba estandarizada.

Qué es el parámetro?

Valor que resume una determinada variable en una población

• Media, porcentaje…

Suelen ser constantes o variables?

• La población es única, así que suelen ser constantes

El parámetro sería la diferencia real en la media de las notas entre todos los estudiantes universitarios que toman apuntes con portátil y todos los que toman apuntes con papel.

Qué es estadístico?

Valor que resume una determinada variable en una muestra (nos da una idea de lo que podría ser el parámetro)

Suelen ser constantes o variables?

• La muestra es variable, puede cambiar, entonces esto podrá ser variable también.

Ejemplos:

• Elegir a alguien al azar y preguntar la edad

  • variable

• Elegir a cinco personas al azar y calcular la media de sus edades

  • variables

• Preguntar a toda la clase y hacer la media de sus edades

  • constante

El estadístico sería la diferencia entre las medias de las notas de los dos grupos dentro de tu muestra (la clase o clases donde haces el estudio).

Qué es el muestreo?

Técnicas para seleccionar una muestra de una población

Hay diversas formas de seleccionar la muestra. Conocer la población será clave para hacerlo de unas maneras u otras.

Opciones posibles según tu diseño:

• Muestreo aleatorio simple: seleccionar estudiantes al azar.

• Muestreo por conveniencia: usar los estudiantes disponibles en una clase (muy común en estudios educativos).

• Muestreo estratificado: asegurar que haya representación equilibrada de quienes usan portátil y quienes usan papel.

Qué es la estadística descriptiva?

Describir los datos después de haberlos analizado (Parte de la estadística que se dedica a recoger, clasificar, resumir y analizar un conjunto de datos, con el fin de describir ese conjunto)

• No nos dice mucha cosa porque imaginemos que nos da de media de a cuánto vivimos de clase, 30min. Esto puede significar que o todos vivimos a 30min o que unos están muy cerca y otros muy lejos.

En tu estudio incluiría:

• Media y desviación estándar de las notas en cada grupo.

• Distribución de estudiantes por método de toma de notas.

• Gráficos comparativos (barras, boxplots).

Ejemplo:

• Media del grupo portátil = 6.8; media del grupo papel = 7.5.

Inferencia

Conjunto de métodos usados para obtener conclusiones sobre al población a partir de la información obtenida de una muestra.

Permiten generalizar los resultados de la muestra a la población

• Hay que tener en cuenta si la diferencia entre nuestros datos x% y z% es muy grande o muy pequeña → si la diferencia es muy pequeña puede ser casualidad. 

En este caso:

• Prueba t de Student para comparar medias entre dos grupos.

• Intervalos de confianza para la diferencia de medias.

• Decisión sobre la hipótesis (rechazar o no rechazar H₀).

Ejemplo:

• Si p < 0.05, se concluye que existen diferencias significativas en el rendimiento académico según el método de toma de notas.

Qué es la probabilidad?

Rama de las matemáticas que mide la posibilidad de que se dé el resultado en una variable.

Variable

Característica observable en los individuos que pude tomar valores diferentes.

• La variabilidad es la capacidad de variar de esa característica

Fuentes de variabilidad:

• Medida

  • Instrumento

  • Observador

• Biológicas

  • Intra individuos

  • Entre individuos

Fuentes de variabilidad: de instrumento

Herramienta que uso para medir la variable

No debería añadir variabilidad; a un mismo individuo medido dos veces debe dar el mismo resultado (fiabilidad) y además el resultado debe ser el correcto (validez)

Ejemplo:

• Para calcular el nivel de inteligencia les haces un examen a los alumnos, este examen será el instrumento para calcular la variable así que un examen no puede ser más difícil que el otro.

Fuentes de variabilidad: observador

El observador que recoge la medición puede añadir variabilidad

Necesitamos lo mismo que necesitábamos en instrumento:

• Fiabilidad

• Validez

Ejemplo:

• tipo de examen, varía dependiendo del profesor que lo corrige - Si el examen es tipo test → este ya no tienen efecto (no varia)

Fuentes de variabilidad: intra individuos

Todos los valores por el que el mismo individuo puede dar valores diferentes (y ser correctos)

• La hora del día, si acaba de comer, etc…

• Para ello se hacen todas las mediciones en las mismas condiciones.

Entre individuos

Todos los motivos por los que dos individuos pueden dar resultados diferentes.

Estas fuentes de variabilidad son inevitables dada la condición humana

VARIABLES. Tipos según su papel en el análisis

Variable dependiente (outcome o respuesta):

• la de interés. Afectada (o no) por las variables independientes. Es lo que queremos demostrar.

Variables independientes (predictoras o explicativa):

• la que puede tener un efecto sobre la dependiente según la hipótesis

Covariables

• otras variables que pueden influir en la variable dependiente y de ese modo influir en nuestro resultado. Se deben controlar, ajustar o estratificar

VARIABLES. Según tipo y escala

Variables según tipo de escala pueden ser:

Cualitativas (representan características o atributos que no son numéricos. Sus posibles valores se llaman categorías. Suelen ser pocos y por tanto repetirse)

• Escala nominal (≠)

• Escala ordinal (≠, >)

Cuantitativas (discretas/continuas)

• Discretas: toman valores finitos y concretos (si tenemos o no hermanos, el valor del café pq este siempre tiene que tener un valor exacto…)

• Continuas: toman cualquier valor dentro de cierto intervalo. Siempre se redondean (edad, altura, porque se redondean)

  • Intervalo

  • Razón

Las variables discretas a menudo toman pocos valores, y por lo tanto se repiten. Con las continuas, no suele ser así

Problema con cualitativas y cuantitativas

Las variables continuas tienen el problema de que podríamos no parar de medir, si digo que mi altura es 1,70, podría medir más decimales (1,70,678483929… y podría no parar), esto es una locura, así que diciendo solamente los cm me valen, aunque no sea mi altura exacta, lo mismo pasa con la edad.

Cualquier variable continua la mediremos así, aproximando.

Muchas veces las variables se recodifican: se convierten de cuantitativas a cualitativas ordinales

• Edad (en años)→ <menons de 35 años>, <de 35 a 65 años>, <más de 65 años>

• Hijos → <ninguno>, <Uno>, <dos o más>

— Perdida de información

• La clasificación es adecuada?

• Guardar siempre la variable original

• Siempre estamos a tiempo

Variable en escala nominal

El valor no tiene ningún orden

Dos individuos pueden ser iguales:

Ejemplo:

• medio de transporte para llegar a la universidad

• Color de ojos

• Universidad donde se estudia

Variable en escala ordinal

Lo mismo que en escala nominal sólo que hay orden.

Se pueden ordenar los individuos

Ejemplo:

• nivel de estudios

• nivel de inglés (A1, A2, B1, B2…), escala de baja, normal o alto

  • No solo comparo, sino que ordeno, su nivel no es solo C2, sino que es también mayor que el mío.

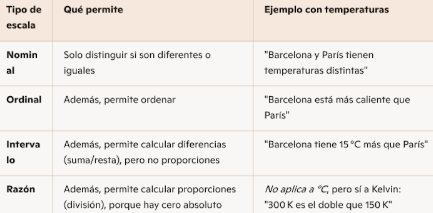
Variable en escala de intervalo

Además de todo lo anterior, podemos calcular la diferencia entre dos individuos, pero no dividirlo, ya que no existe el cero natural.

Ejemplo:

• Temperatura, la hora del día…

Variable en escala de razón

además de lo anterior, podemos dividirlos. La gran mayoría de variables numéricas (cuantitativas) son de este tipo. Cuando el cero indica ausencia de algo.

Explicación de por qué uno se puede dividir y el otro no

1. La Tº: hoy estamos en bcn a 30º y en parís están a 15º, que las temperaturas son diferentes (nominal), podemos decir que una es mayor (ordinal), hacer resta, decir cual hace más frío PERO no podemos dividir y decir que hace el doble de nada porque los 0º es un número arbitrario 

   • (Por qué no se puede dividir con grados Celsius?
     Porque 0 °C no representa ausencia de temperatura, sino un punto arbitrario en la escala. Por eso, decir que 30 °C es el doble que 15 °C no tiene sentido en términos físicos. En cambio, la escala Kelvin sí tiene cero absoluto, lo que permite comparaciones de razón)

2. El sueldo: ella cobra el doble que yo → 0 es la ausencia de dinero