Studied by 22 people
What is a limit?
A limit is a fundamental concept in calculus that describes the behavior of a function as its input approaches a certain value. It represents the value that a function approaches(expected value) as the input gets arbitrarily close to a particular point. Sometimes there is no expected value so we write does not exist or dne.
Lim x → 0+ f(x) = 5means what when spoken out loud?
The limit as x approaches 0 from the right of f(x) is equal to 5.
A limit of f(x) at x = a exist if…?
A limit of f(x) at x = a exists if the left-hand limit and the right-hand limit of f(x) as x approaches a are equal.
Whats the difference between f(a) and lim of f(x) as x approaches a
The main difference between f(a) and the limit of f(x) as x approaches a is that f(a) represents the value of the function f at a specific point a, while the limit of f(x) as x approaches a represents the behavior of the function as x gets arbitrarily close to a. In other words, f(a) is a single value, whereas the limit of f(x) as x approaches a may or may not exist, and if it does, it can be different from f(a).
Suppose lim as x approaches a = f(a) for all a in the domain of f(x). What must be true about f(x)?
For lim as x approaches a = f(a) to hold for all a in the domain of f(x), f(x) must be continuous at every point in its domain.
What does it mean for a graph to oscilate?
A graph oscillates when it repeatedly moves back and forth between two points or values. It shows periodic behavior with regular cycles of highs and lows.
What is direct substitution?
Direct substitution is a method used in calculus to evaluate limits of functions. It involves replacing the variable in the function with the value it is approaching, and then simplifying the expression to find the limit. This method is applicable when the function is continuous at the point being evaluated.
When will a rational function have a hole?
A rational function will have a hole when there is a factor that cancels out in both the numerator and denominator, resulting in an undefined point. This occurs when there is a common factor that can be canceled out, creating a hole in the graph.
When will a rational function have a vertical asymptote?
A rational function will have a vertical asymptote at a value of x where the denominator of the function becomes zero.
How do you find the horizontal asymptote of a rational function?
The horizontal asymptote of a rational function can be found by comparing the degrees of the numerator and denominator. If the degree of the numerator is less than the degree of the denominator, the horizontal asymptote is y = 0. If the degrees are equal, the horizontal asymptote is the ratio of the leading coefficients. If the degree of the numerator is greater than the degree of the denominator, there is no horizontal asymptote.
Explain using limit definition of a horizontal asymptote to explain why a horizontal asymptote can be crossed.
Horizontal Asymptote: A line that a function approaches as x approaches positive or negative infinity. It can be crossed if the function has a removable discontinuity or a vertical asymptote at a certain point. The limit definition of a horizontal asymptote helps us understand that even though the function approaches the asymptote, it does not guarantee that it cannot cross it.
How do we determine if a function is continuous?
A function is continuous if it has no jumps, holes, or breaks. It means that the function is unbroken and can be drawn without lifting the pen. To determine if a function is continuous, we need to check three conditions: 1) the function is defined at the point, 2) the limit of the function exists at that point, and 3) the limit equals the function value at that point.
What is a jump discontinuity?
A jump discontinuity occurs when a function has a sudden change in value at a specific point. The function "jumps" from one value to another without any intermediate values. It is characterized by having two distinct one-sided limits that do not equal each other.
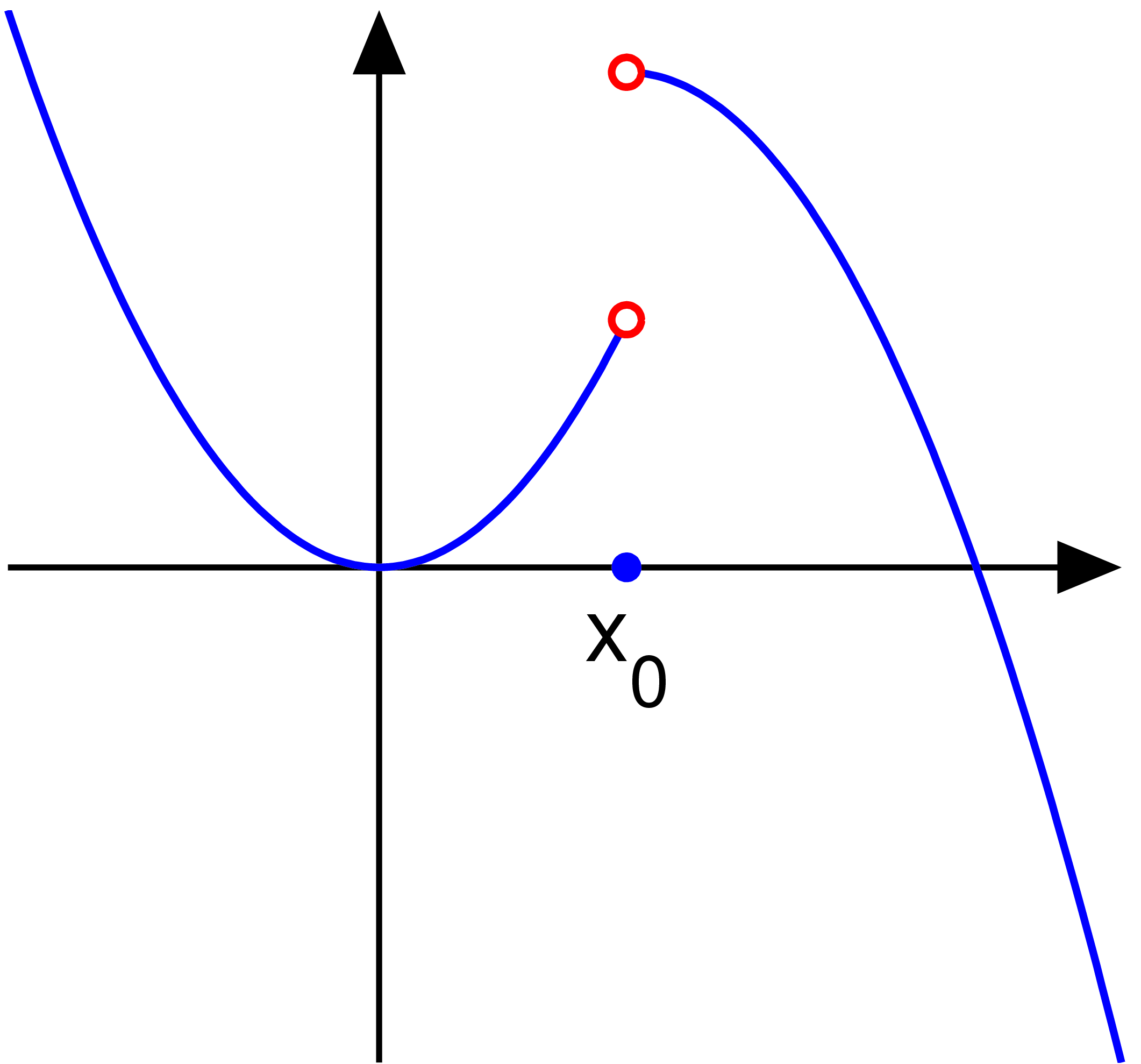
What is a removable discontinuity?
A removable discontinuity is a point on a graph where a hole exists. It occurs when a function is undefined at a certain point, but can be made continuous by assigning a value to that point. The hole can be filled by removing the discontinuity and connecting the graph smoothly.(Black dot is part of the line, white is the hole)
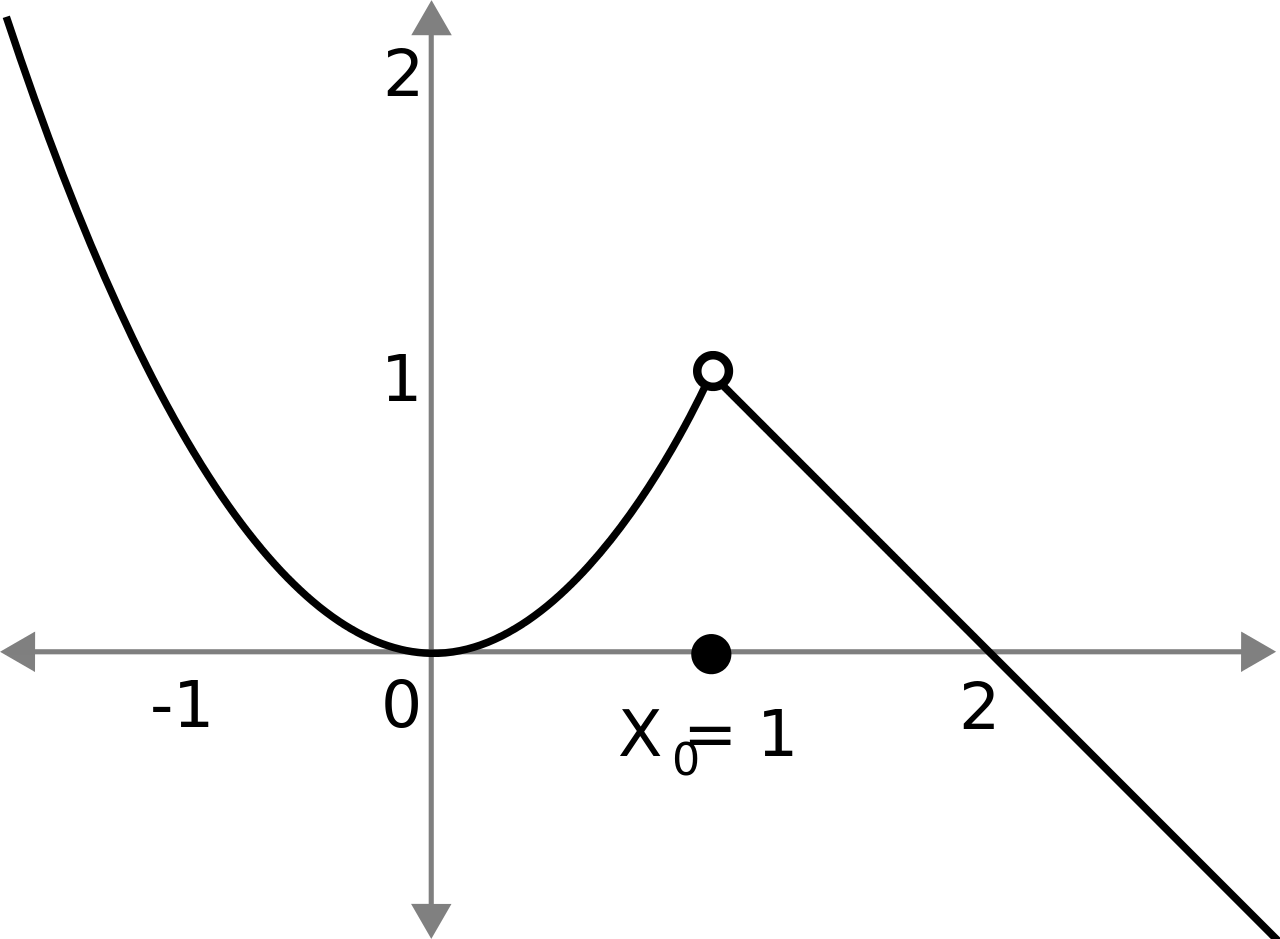
What is a infinite discontinuity?
A type of discontinuity where the limit of a function does not exist because it approaches positive or negative infinity.
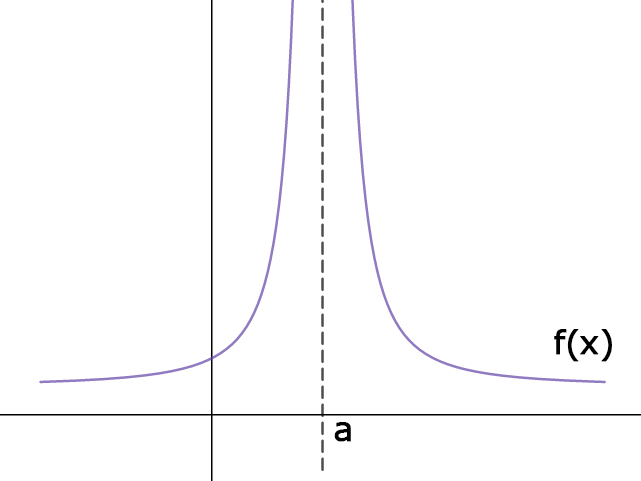
What is a continuity?
A continuity is the property of a function where there are no breaks, holes, or jumps in its graph. It means that the function is smooth and can be drawn without lifting the pen.
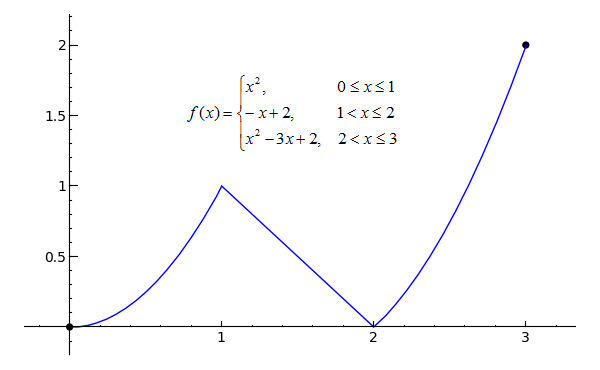
A function is continuous at x = a if __________________________________________________A function is continuous on an open interval (a,b) if it is continuous at all points in the interval. A function that is continuous on the entire real line (−∞, ∞) is continuous everywhere. A discontinuity at a is called removable if f can be made continuous by redefining f(a). Otherwise the discontinuity is_______________
lim of f(x) as x approaches a = f(a), non removable.
What us the Scalar multiple of properties of limits?
Scalar Multiple Property of Limits: When evaluating the limit of a function multiplied by a scalar, the limit is equal to the scalar multiplied by the limit of the function.
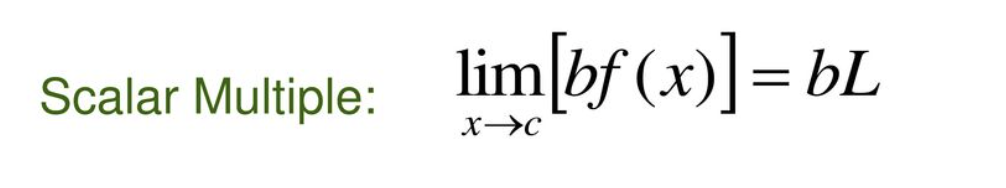
What is the Sum or Difference of properties of limits?
Sum law for limits states that the limit of the sum of two functions equals the sum of the limits of two functions. Difference law for limits states that the limit of the difference of two functions equals the difference of the limits of two functions.
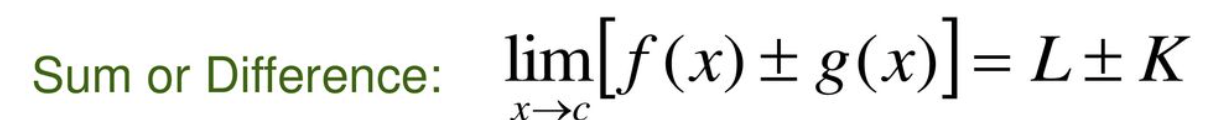
What is the product of properties limits?
Multiply limits of each function.
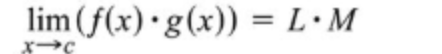
What is the quotient of properties limits?
divide the limits
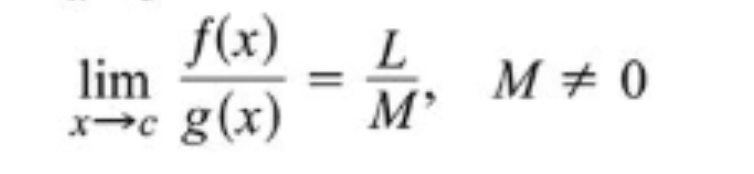
What is the power of properties limits
Raise the limit to the nth power
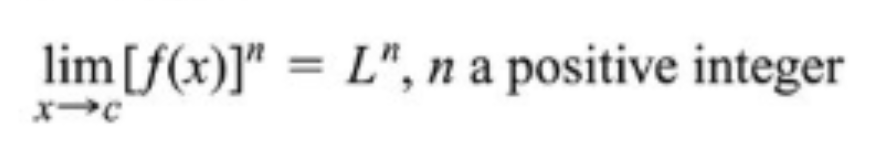
What is squeeze theorem?
The squeeze (or sandwich) theorem states that if f(x)≤g(x)≤h(x) for all numbers, and at some point x=k we have f(k)=h(k), then g(k) must also be equal to them.
What is the intermediate value theorem?
Basically from [a,b] you can find a k that is equal to f( c ) c being in [a,b]
Note 
Flashcard (43)