Alternating Series Error Bound Theorem

The Alternating Series Error Bound Theorem is an essential concept in AP Calculus, particularly in the study of series and approximations. This theorem provides a way to estimate the error when using a partial sum to approximate the sum of an alternating series. Below is an in-depth exploration of this theorem, its applications, and related concepts.

1. Definition of an Alternating Series

An alternating series is a series where the terms alternate in sign. It is typically expressed as:

2. Convergence Conditions (Alternating Series Test)

An alternating series converges if it satisfies the following two conditions:

1. Monotonicity:
   The terms ana_nan​ are monotonically decreasing

   ex.

   

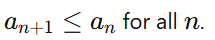
2. Vanishing Term Condition:

   

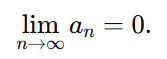
If these are satisfied, the series converges by the Alternating Series Test (Leibniz Criterion).

3. Error in Partial Sums

4. The Alternating Series Error Bound Theorem

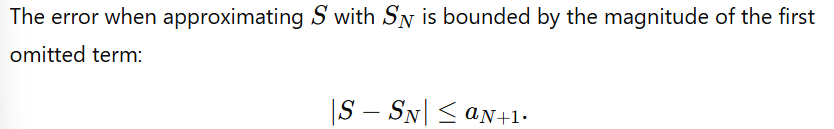
• The error bound is absolute, meaning it ignores the sign of the terms.

• The error is directly related to the size of the next term in the sequence, aN+1a_{N+1}aN+1​.

• This makes alternating series particularly useful for approximations, as the error is easy to control and calculate.

5. Examples

Example 1: Alternating Harmonic Series

Example 2: Alternating Series with Smaller Terms

6. Practical Applications

1. Approximating Series Sums: The error bound ensures that we can control the accuracy of approximations for alternating series.

2. Numerical Methods: The theorem is widely used in numerical analysis, particularly when calculating transcendental functions such as

   

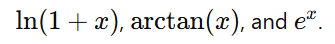
3. Engineering and Physics: In contexts where infinite series appear, alternating series often emerge, and the error bound ensures that approximations meet desired precision.

7. Importance in AP Calculus

• Conceptual Understanding: Helps students grasp the relationship between convergence and error.

• AP Exam Applications: Frequently appears in multiple-choice and free-response questions, requiring calculations and explanations of error bounds.

• Connection to Taylor Series: Alternating series often connect to the error bounds of Taylor polynomial approximations.

8. Summary

The Alternating Series Error Bound Theorem is a simple yet powerful tool for approximating the sum of an alternating series. It provides a clear guideline for controlling error, making it invaluable in calculus and beyond. Its practical applications and conceptual clarity make it a cornerstone of series approximation techniques.

By understanding this theorem, students can confidently tackle problems involving alternating series and make precise approximations with minimal effort.