Introduction

• Kinematics is the branch of physics that studies the motion of objects without considering the forces causing the motion.

• One-dimensional kinematics deals with motion along a straight line, considering only one direction.

2.1: Displacements

• Kinematics

  • Deals with the concepts that are needs to describe motion. without any reference to forces.

  • How things move

  • Straight line motion

• Dynamics deals with the effect that forces have on motion

• Kinematics and dynamics from the branch of physics we know as mechanics.

• Displacement visual:

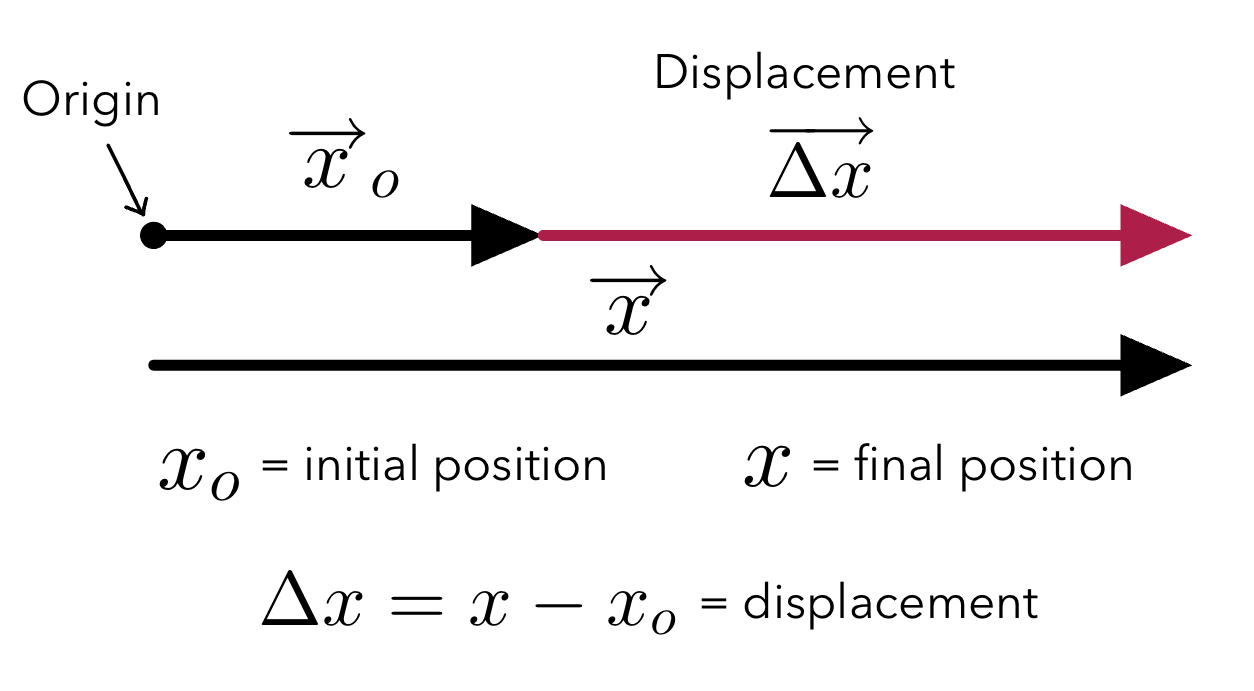Variable Meanings:

• {x}_{0} = initial position

• x = final position

• \Delta = final - initial

  • Change in

• \Delta x=x-x_{0}

• Arrows over variable represent vectors

2.2: Speed and Velocity

Average speed

• Average speed is the distance traveled divided by the time required to cover the distance.

  • Average speed = \dfrac{Distance}{ElapsedTime}

  • Elapsed time = \Delta t=t-t_{0}

• Distance (m)

  • A scalar unit measure of the distance an object moves as measured along the path followed.

• Scalar quantity

• SI units for speed: \dfrac{m}{s}

Average velocity

• Average velocity is the displacement divided by the elapsed time.

  • Average velocity = \dfrac{Displacement}{ElapsedTime} = \dfrac{\Delta \overrightarrow{x}}{\Delta t}

    • \Delta x=x-x_{0}

    • \Delta t=t-t_{0}

• If average velocity is positive, the object is moving in the positive direction.

• If average velocity is negative, the object is moving in the negative direction.

• If average velocity is zero, the object is not moving.

• Displacement (m)

  • A vector representing the change in position of an object, drawn from the initial to the final position.

• Vector quantity

• SI unit for velocity: \dfrac{m}{s}

Instantaneous velocity

• The instantaneous velocity indicates how fast an object is moving and the direction of motion at each instant of time.

• The rate of change of the displacement at a particular instant.

• \overrightarrow{v}=\lim _{\Delta t-0}\dfrac{\overrightarrow{\Delta x}}{\Delta t}

• Vector quantity

• SI unit for velocity: \dfrac{m}{s}

2.3: Acceleration

• Acceleration is any change in velocity for an object divided by the time interval over which the change occurs.

• The notion of acceleration emerges when a change in velocity is combined with the time during which the change occurs.

• The change in the velocity of an object divided by the elapsed time.

• Definition of average acceleration:

  • \dfrac{}{\overrightarrow{a}}=\dfrac{\overrightarrow{v}-\overrightarrow{v}_{0}}{t-t_{0}}=\dfrac{\Delta \overrightarrow{v}}{\Delta t}

• If average acceleration is positive, the speed is increasing with time.

• If average acceleration is negative, the speed is decreasing with time.

• If average acceleration is zero, it is at constant speed.

• Vector quantity

• SI unit for velocity: \dfrac{m}{s^{2}}

2.4: Equations of Kinematics for Constant Acceleration

• Develop useful equations assuming:

  • Acceleration is constant

  • Start motion at origin

  • Start clock at time = 0

• Five kinematic variables

  Meaning	Variable	Units
  Displacement	x	m
  Acceleration (constant)	a	\dfrac{m}{s^{2}}
  Final velocity (at time t)	v	\dfrac{m}{s}
  Initial velocity	v_{0}	\dfrac{m}{s}
  Elapsed time	t	s

• Kinematic equations

  • v=v_{0}+at

  • x=\dfrac{1}{2}\left( v_{0}+v\right) t

  • v^{2}=v_{0}^{2}+2ax

  • x=v_{0}t+\dfrac{1}{2}at^{2}

2.5: Applications of the Equations of Kinematics

Reasoning Strategy

• Make a drawing.

• Decide which directions are positive and negative.

• Write down the value that are given for any of the five kinematic variable.

• Determined the desired variable.

  • Each equation has only 4 variables.

  • If we know 3, we can solve for the rest.

• Find the appropriate kinematic equation to apply.

• Solve.

2.6: Freely Falling Bodies

• Free Fall - An idealized vertical motion in which air resistance is IGNORED.

• All bodies at the same location above the Earth fall vertically with the same acceleration.

• This motion of free fall and the acceleration of a freely falling body is called acceleration due to gravity.

• Acceleration due to gravity is always constant and always faces downwards.

  • The ONLY force acting on the object is the CONSTANT FORCE OF GRAVITY.

  • Causes constant acceleration of -9.80 m/s²

    • a =-9.80 m/s²

    • g = 9.80 m/s²

      • g is ALWAYS positive.

• If a ball is thrown in the air, gravity is pulling it down.

Graphical Analysis of Velocity and Acceleration-Velocity

• Slope = \dfrac{rise}{run}=\dfrac{\Delta x}{\Delta t}=\overline{v}

ON A DISPLACEMENT-TIME GRAPH

• SLOPE equals VELOCITY (rise/run)=m/s)

• Y-INTERCEPT equals the INTIAL DISPLACEMENT

• STRAIGHT LINES imply zero velocity (constant velocity)

• CURVED LINES imply non-uniform acceleration

• PARABOLIC LINES imply constant acceleration

• AVERAGE VELOCITY is the slope of the straight line connecting the endpoints of a curve

• INSTANTANEOUS VELOCITY is the slope of the line tangent to a curve at any point

• POSITIVE SLOPE implies motion in the positive direction

• NEGATIVE SLOPE implies motion in the negative direction

• ZERO SLOPE implies state of rest

ON A VELOCITY-TIME GRAPH

• SLOPE equals ACCELERATION (rise/run = m/s / s=m/sa²)

• Y-INTERCEPT equals the INITIAL VELOCITY

• HORIZONTAL LINES imply zero acceleration

• STRAIGHT LINES implyconstant acceleration

• CURVED LINES imply non-uniform acceleration

• AVERAGE ACCELERATION is the slope of the straight line connecting the endpoints of a curve

• INSTANTANEOUS ACCELERATION is the slope of the line tangent to a curve at any point

• POSITIVE SLOPE implies an increase in velocity in the positive direction

• NEGATIVE SLOPE implies an increase in velocity in the negative direction

• ZERO SLOPE implies motion with constant velocity

ON AN ACCELERATION-TIME GRAPH

• SLOPE is meaningless, but zero slope (a horizontal line) implies motion with zero or constant acceleration

• Y-INTERCEPTS equals the initial acceleration

• The area under the curveequals the change in velocity (m/s² x s = m/s)

Extra Notes

Constant Acceleration

• Constant acceleration refers to a situation where an object's velocity changes by the same amount in each unit of time. In other words, the object's acceleration remains constant over time. This can be represented by a straight line on a velocity-time graph.

• If something is speeding up in a given direction, the acceleration must be in that direction.

• If something is slowing down, the acceleration is opposite to the direction of motion.

Example: A car moving along a straight road with constant acceleration can be exemplified by a scenario where its velocity increases by 10 m/s every second. Initially, the car is at rest, but after 1 second, its velocity becomes 10 m/s. After 2 seconds, it reaches 20 m/s, and so on. This consistent increase in velocity over time demonstrates constant acceleration.

Freely Falling Bodies

• In absence of air resistance, all bodies near the surface of the Earth fall vertically with the same constant acceleration (because of constant force).

  • This is called the acceleration due to gravity (gravity being the force that causes the acceleration.

  • Represented by symbol g.

• Force of gravity is ALWAYS present.

• Acceleration is ALWAYS present, ALWAYS the same value, and ALWAYS directed downward (toward center of Earth, so its negative if pointing down).

• g = -9.80 m/s²

  • g may be exchanged with a = -9.80 m/s²

• Since the force of air resistance increases with speed, sometimes objects will reach a maximum “terminal velocity” and stop accelerating when at some point net acceleration = 0

Terminal Velocity (v+)

• Terminal velocity is the maximum velocity that an object can reach when falling through a fluid, such as air or water. It occurs when the force of gravity pulling the object downward is balanced by the drag force exerted by the fluid. At terminal velocity, the object no longer accelerates and falls at a constant speed. The value of terminal velocity depends on the object's mass, shape, and the density of the fluid it is falling through.

• EQUATION FOR VELOCITY

  • Velocity = gravity(time)

  • v = gt

• v=g(t) is a vacuum, so v continually increases

Key Concepts

1. Displacement:

   • The change in position of an object.

   • It is a vector quantity, having both magnitude and direction.

   • Symbolized by Δx.

2. Velocity:

   • The rate of change of displacement.

   • It is a vector quantity, having both magnitude and direction.

   • Symbolized by v.

   • Average velocity (v_avg) is calculated as the displacement divided by the time taken.

3. Speed:

   • The rate of change of distance traveled.

   • It is a scalar quantity, having only magnitude.

   • Symbolized by s.

   • Average speed (s_avg) is calculated as the total distance traveled divided by the time taken.

4. Acceleration:

   • The rate of change of velocity.

   • It is a vector quantity, having both magnitude and direction.

   • Symbolized by a.

   • Average acceleration (a_avg) is calculated as the change in velocity divided by the time taken.

5. Equations of Motion:

   • The equations that relate displacement, velocity, acceleration, and time.

   • For constant acceleration, the following equations hold:

     • v = u + at (equation 1)

     • s = ut + (1/2)at^2 (equation 2)

     • v^2 = u^2 + 2as (equation 3)

     • s = ((u + v)/2)t (equation 4)

     • Where u is the initial velocity, v is the final velocity, t is the time, and a is the acceleration.

6. Graphical Representations:

   • Displacement-time graph:

     • The slope of the graph represents velocity.

   • Velocity-time graph:

     • The area under the graph represents displacement.

   • Acceleration-time graph:

     • The slope of the graph represents acceleration.

Conclusion

• One-dimensional kinematics focuses on the motion of objects along a straight line.

• Displacement, velocity, speed, and acceleration are fundamental concepts in kinematics.

• Equations of motion and graphical representations help analyze and understand the motion of objects.