vibrational/infrared spectroscopy

what does vibrational spectroscopy probe

molecular motions due to movement of atoms in individual chemical bonds

EM region for vibrational spectroscopy and what it is used for

IR region

used to identify functional groups in molecules, confirm the structure of compounds and measure the vibrational frequencies and force constants of chemical bonds

vibration of diatomic molecules

• how is it modelled

• equation?

• diagram (3 scenarios)

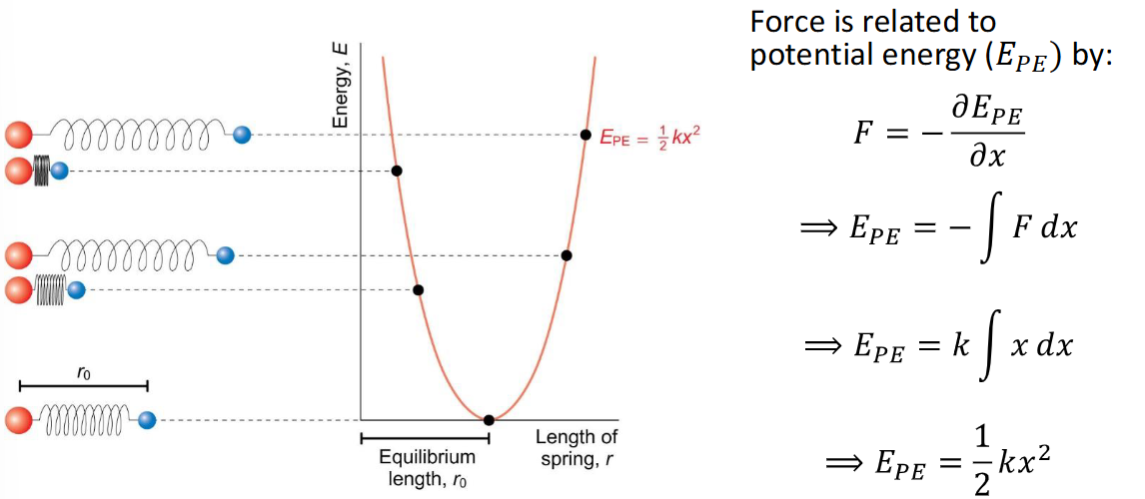
how are potential energy and force related

• equation + derviation

• graph/diagram

vibrational frequency of a diatomic molecule

• the bond oscillates, undergoing simple harmonic motion

• the vibrational frequency depends on

  • mass of atoms - heavier atoms vibrate at a slower frequency

  • bond force constant - stiffer “springs” vibrate at higher frequency

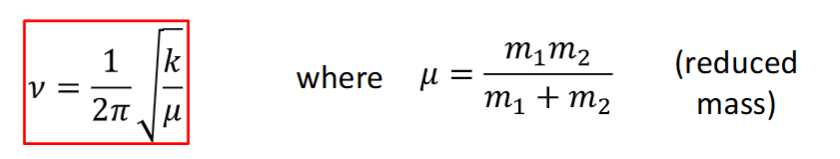
how is the equation for E_V found

what is it and what are the terms

found by solving schrodinger’s equation with V(x) = ½kx²

v is the vibrational quantum number which takes integer values v ≥ 0

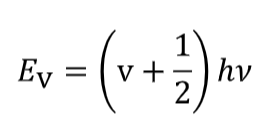
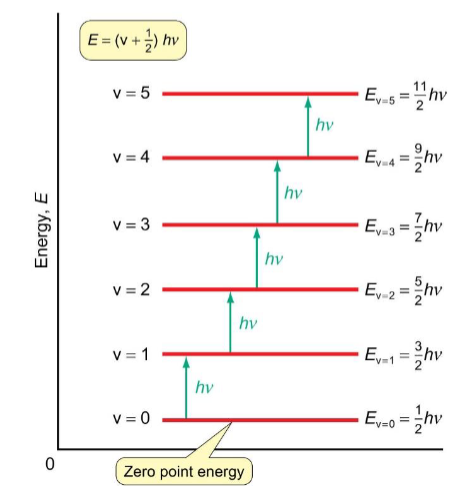
ground state for vibrational energy?

there is a finite ground state energy:

E_V=0 = ½hv - as lowest v=0 → vibrational does not allow zero energy level

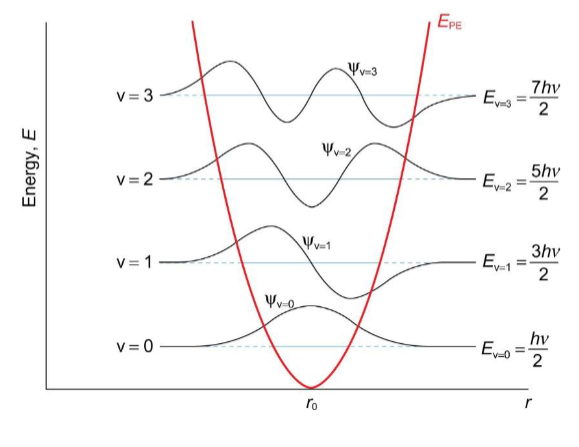
vibrational energy levels and wavefunctions

• wavefunctions are finite outside of the parabolic potential well - an example of quantum mechanical tunnelling

• classically, the particle is forbidden to exist outside the potential well, but there is a finite probability of the particle penetrating this region in quantum mechanics - it continues outside the red line for a short period

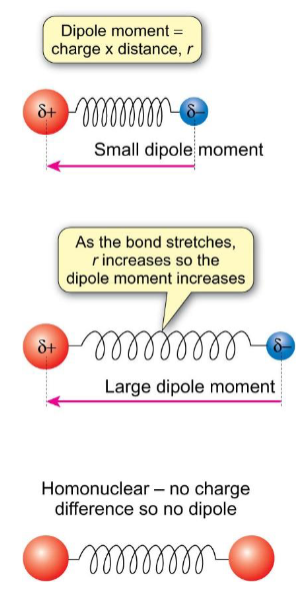
gross selection rule for vibrational

there must be a change in the dipole moment of the molecule during the vibration - for diatomics, this means the molecule must have a permanent dipole moment. homonuclear diatomics eg H₂ do not give IR spectra

specific selection rule for vibrational

Δv = ±1

+1 for absorption and -1 for emission spectra

vibrational spectra of diatomic molecules

• transitions are between adjacent levels - all ΔE = hv

• vibrational spectroscopy can only probe the transitions and the gaps are identical for diatomics, so only one peak is expected in the spectrum

how are bond force constants measured

• force constant is a measure of stiffness and therefore of strength

• combine equations for E_v and v to give this equation

• calculate reduced mass

• k can be calculated from the equation for ΔE

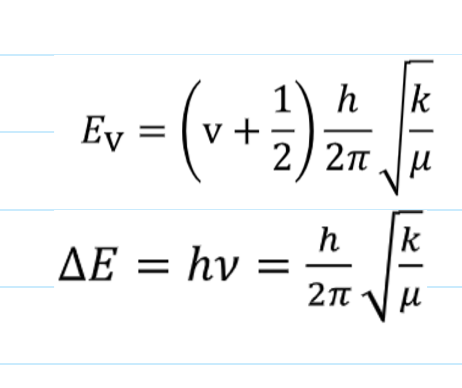
populations of vibrational energy levels

use Botlzmann distribution again

in this case the ground state has approx 2 million times the occupancy of higher states (can usually expect this as expect molecules to be in ground state)

this means the dominant transition, and the one causing the spectrum, is v=0 → v=1 (as can only move out of v=0 and the specific selection rule means can only go to v=1)

effect of isotopic substitution

when is it most significant

the bond force constant is a property of the chemical bond and therefore the electron distribution

this is not expected to change significantly by adding extra neutrons to the nucleus - ie k is assumed to be independent of the isotope

there are slight shifts in spectra, and heavier isotopes cause lower frequencies

the shift in spectra is most significant for H → D isotopic substitution as the lightest atom moves much more than the heavy atom and dominates the value of the reduced mass.

anharmonic vibrations

• when used

• equation (name?)

• graph

assumption of harmonic oscillations is good but not exact. real molecules undergo anharmonic oscillations - energy levels are still in good agreement for low v.

Morse curve/Morse potential

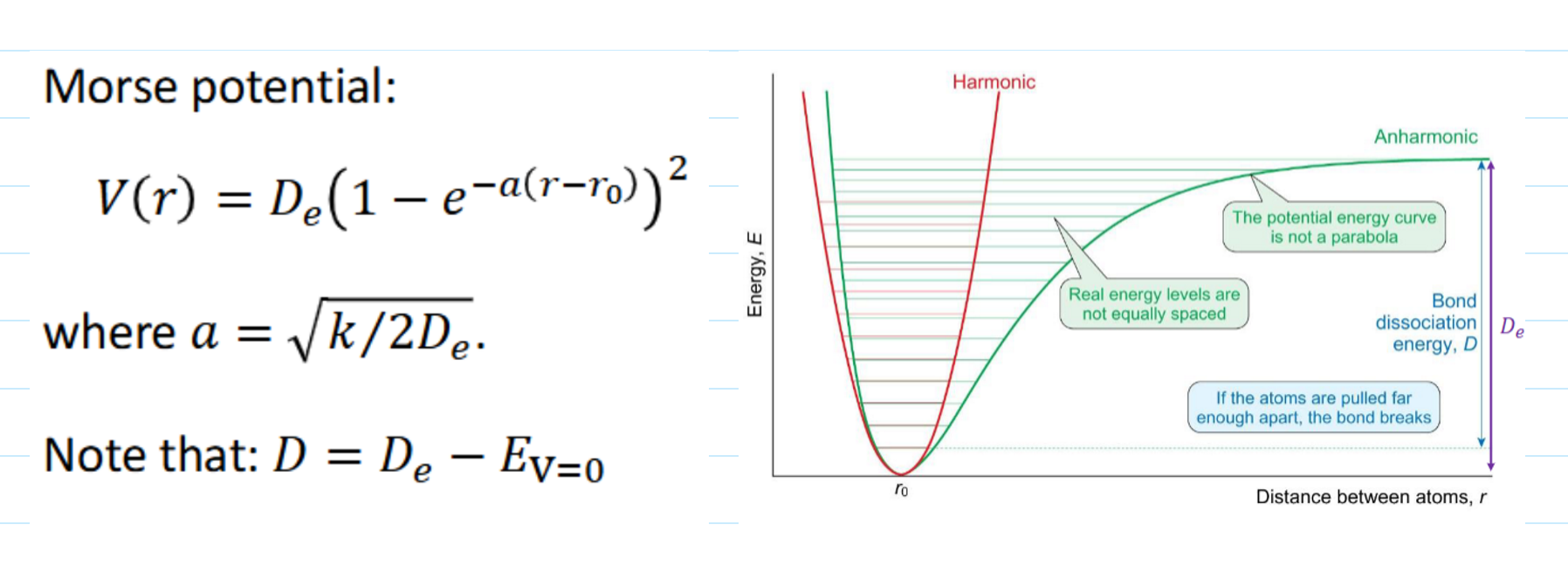
energy levels for anharmonic oscillators

what happens as v increases

ΔE gets smaller as v increases

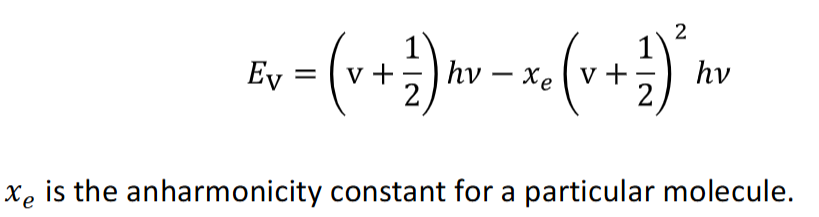
what are overtones

the selection rule Δv = ±1 is strictly for harmonic oscillators

for anharmonic oscillations in real molecules, transitions v=0 → v=2 and v=0 → v=3 are observed. these are called overtone bands and occur at twice and three times the fundamental frequency - however they are much weaker than the fundamental absorption v=0 → v=1

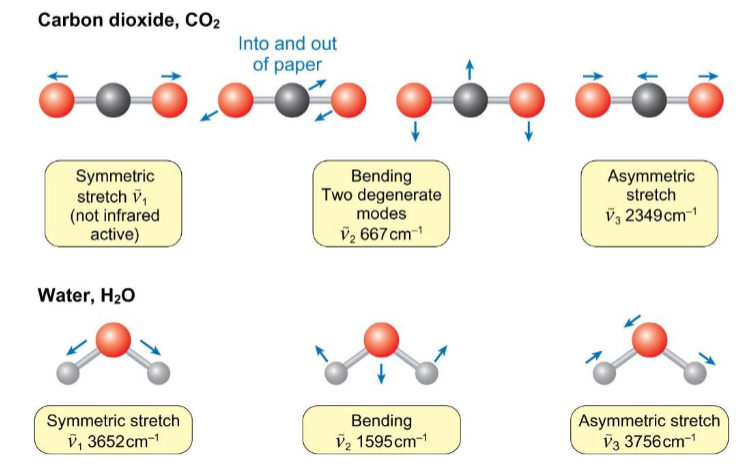
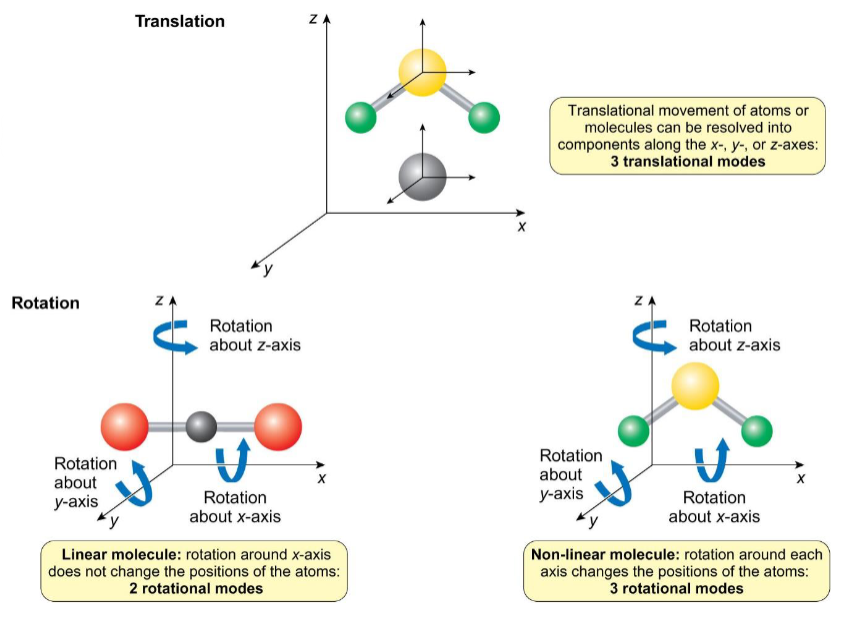
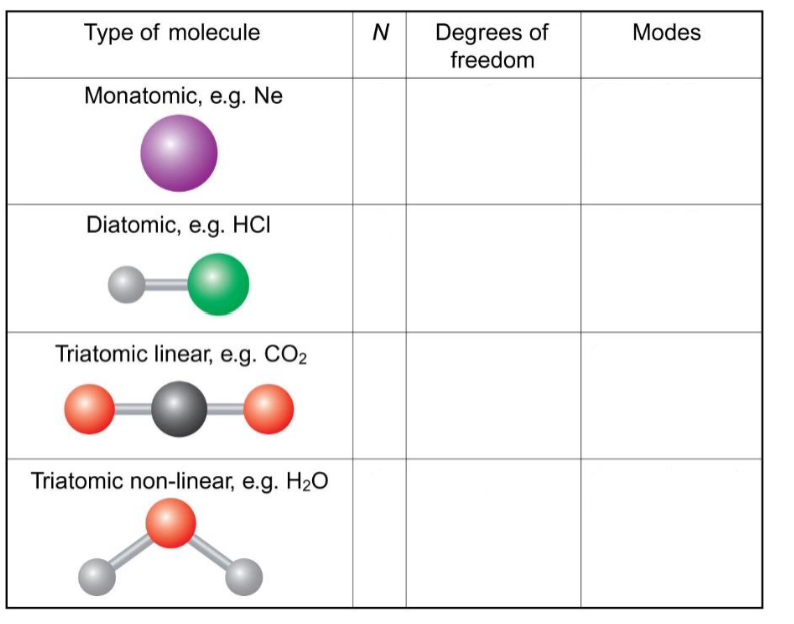
polyatomic molecules

there are vibrational modes due to bending (changes in bond angle) as well as symmetric and asymmetric stretches

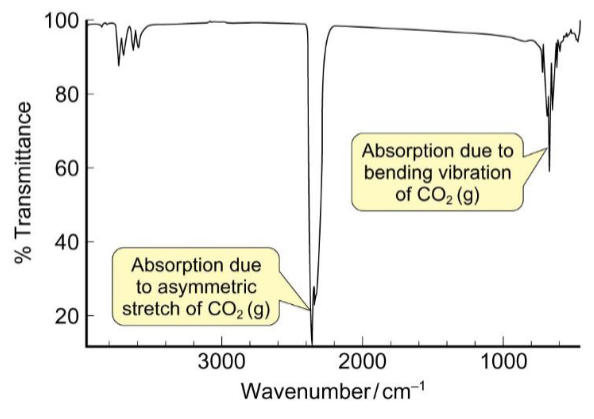
how are atmospheric concentrations of CO₂ measured

the symmetric stretch of CO₂ does not change the dipole moment so its not IR-active

the absorption of the asymmetric stretch can be used for atmospheric measurement of CO₂ concentrations

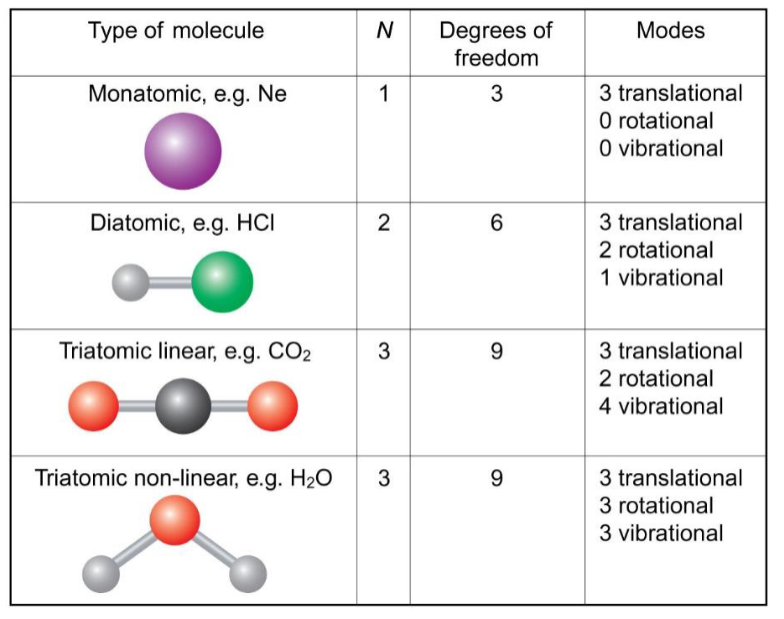
vibrational modes of N atom molecules

more atoms = more possible modes of vibration

linear molecules have (3N-5) vibrational modes

non-linear molecules have (3N-6) vibrational modes

each vibrational mode has its own potential energy curve and series of vibrational energy levels

degrees of freedom

N atoms have 3N degrees of freedom

complete