3.12.2 Wave-particle duality

Newtons corpuscular theory of light

Newton proposed light was made up of small particle-like bodies called corpuscles.

How did Newton explain reflection and how did he state the velocity of the corpuscles change?

• The corpuscles hit the reflective surface and experience an equal and opposite repulsive force from the surface following Newtons third law.

• Horizontal component of velocity unchanged.

• Vertical component of velocity changed.

How did Newton explain refraction and how did he state the velocity of the corpuscles changes?

• Short range force of attraction to surface of more dense medium such as air to glass.

• The component of velocity/momentum parallel to surface unchanged.

• Component perpendicular to surface increases

• Light bends towards the normal / angle of refraction < angle of incidence

• light travels faster in glass than air as it is more dense.

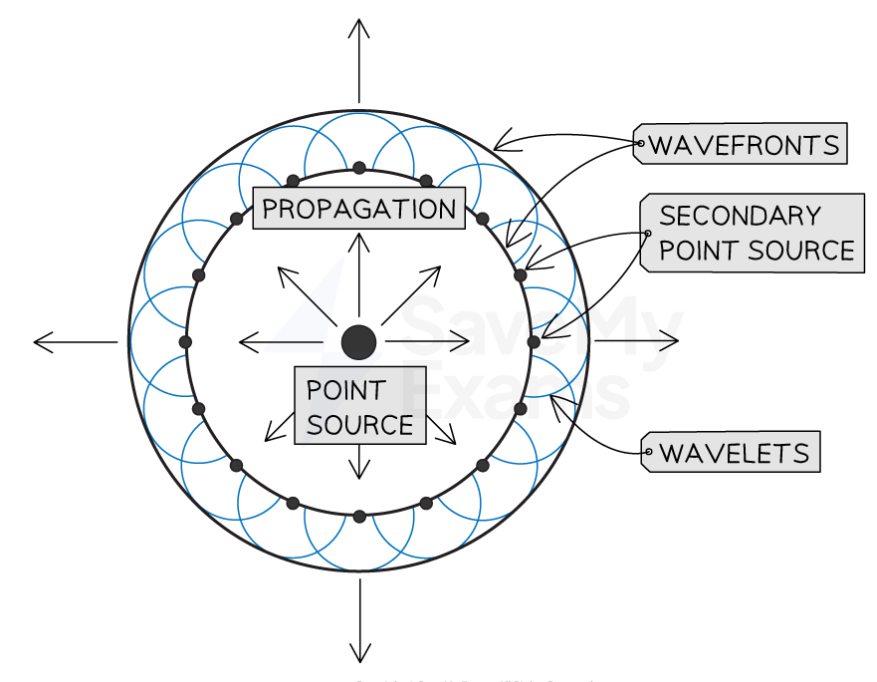
Outline the key features of Huygens’ theory

• Light is a wave.

• The theory uses the idea of secondary wavelets.

• Every point on wavefront acts as a point source of secondary wavelets.

• Secondary wavelets spread out to form the next wavefront.

How did Huygens explain reflection?

• Wavefront hits a reflective surface.

• The point of reflection becomes a secondary point for new wavelets.

• Different parts of the wavefront hit the reflective surface at different times.

• The wavelets spread away from the surface and re-join with others to reform the reflected wavefront in a new direction.

How did Huygens explain refraction of light at an interface between air and water?

• Wave front is incident on interface.

• Huygens secondary wavelets at wave fronts.

• Wavelets travel more slowly in the water.

• The slowing down of the waves / wavelets causes the change in direction.

3 reasons why Newtons theory was preferred

• Newton had a very high reputation at the time.

• There was no way of measuring the speed of light at the time.

• There was no way of observing diffraction at the time.

Youngs double slit experiment explained in terms of Huygens wave theory of light

• When wave reaches slit each point at slit produces secondary wavelets.

• Wavelets overlap on screen.

• Path difference due to different distances between a point on the screen and the two slits.

• Path difference introduces phase differences.

• Bright fringes form where path difference is whole number of wavelengths/waves arrive in phase.

• Dark fringes where path difference is odd number of half wavelengths/waves arrive in antiphase.(Do not accept ‘out of phase’.)

Delayed acceptance of Huygens’ wave theory of light.

• Even after the Young’s double slit experiment, which disproved corpuscular theory, Huygen’s theory wasn’t widely accepted because Newton was a historical figure who scientists expected to be correct.

• It wasn’t until the speed of light was measured in water that Newton’s theory was disregarded, because it was found that light travels slower in water which contradicts the corpuscular theory of light.

Nature of electromagnetic waves

Alternating magnetic and electric fields travelling in phase and at right angles to each other. The direction of wave travel is perpendicular to the oscillations of the electric and magnetic fields.

Maxwells formula for electromagnetic waves

• c=1/√μ₀ε₀

• Here, μ₀ is the permeability of free space, a constant

• ε₀ is the permittivity of free space, also a constant (which has already been encountered in the Electric Fields topic)

• Both of these values are constant, so the speed of electromagnetic waves in a vacuum is constant

• The permeability of free space, μ₀ is a constant that relates magnetic flux density with the current in free space that produces the field

• The permittivity of free space, ε₀ similarly is a constant that relates electric field strength with the charged object in free space producing the electric field.

How did Hertz discover radio waves

• Hertz discovered radio waves by using an apparatus which allowed high voltage sparks to jump across a gap of air as this leads to the production of radio waves.

• The radio waves could be detected by using a loop of wire with a gap.

• This will detect the waves’ alternating magnetic field as the field will enter the loop causing a change in magnetic flux, inducing a potential difference which will cause a spark to cross the gap in the wire.

How did Hertz measure the speed of radio waves

• By placing a metal sheet in front of the apparatus, the radio waves are reflected back onto themselves causing stationary waves to be formed.

• By using detectors, you can find the distance between adjacent nodes (points of no displacement) in order to find the wavelength, and using the frequency of the waves, calculate their speed.

Significance of Hertz measurement of the speed of radio waves

The speed calculated by Hertz was found to be the same as Maxwell’s predicted value of the speed of electromagnetic waves, which helped confirm that radio waves were EM waves.

Fizeau’s determination of the speed of light

• A pulsed beam of light is passed through a gap in a toothed wheel rotating at a slow speed.

• The beam of light reflects on a mirror a large distance behind the wheel causing it to return back through the same gap between teeth in the wheel.

• The speed of rotation of the wheel is increased until the light beam can no longer be seen because it is blocked by a tooth in the wheel next to the gap it could previously pass through. (If this speed is doubled, the light would be visible again because the light will now return through the gap next to the one it initially passes through).

• The toothed wheel has n  gaps and n  teeth which both have the same width

  • This means that, if a full revolution has a period of T, then the time taken for a gap to be replaced by a tooth is 𝑡 = 𝑇/2𝑛

• Recall that time period is the reciprocal of frequency f  (of teeth passing a point per second) so we can write this as 𝑡 = 1/2𝑛𝑓

• When the observer sees the reflected light disappear, the time taken for light to travel the distance to the mirror and back (2d) is the time taken for a gap to be replaced by a tooth (t), so 2𝑑/𝑐 = 1/2𝑛𝑓

• Rearranging this allowed Fizeau to calculate the speed of light as 𝑐 = 4𝑑𝑛𝑓

Implications of Fizeau’s determination of the speed of light

Fizeau’s result was extremely significant because it was very close to the value predicted by Maxwell, which provided evidence that light was an EM wave.

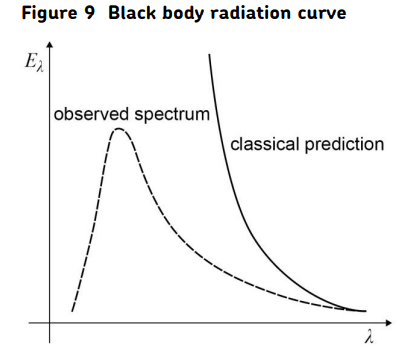
The ultraviolet catastrophe and black-body radiation.

• The ultraviolet catastrophe refers to the disagreement between practical measurements of the energy intensity at different wavelengths from a black body at a given temperature and the theoretical predictions using classical physics.

• A black body is one that emits all wavelengths of radiation that are possible for that temperature.

• The dotted lines in the graph in Figure 9 show the practical variation of energy intensity emitted at different wavelengths with wavelength for a particular temperature.

• The solid line shows the prediction made using classical physics. Classical physics predicts that most of the energy would be emitted at short (ultraviolet) wavelengths and would become infinite at very short wavelengths.

• Measurements indicate however that there is a peak as shown by the solid line. This peak occurs at a shorter wavelength as the temperature increases (Wein’s Law).

Planck’s interpretation in terms of quanta

• EM radiation emitted in quanta.

• Energy of quantum is related to a single frequency E=hf.

Outcomes of photoelectric effect experiment

• No photoelectric emission if incident light below threshold frequency.

• Photoelectric emission is instantaneous/occurs as soon as light is incident on metal surface

• Photoelectrons have a range of KE from zero to max value, depending on type of metal and frequency of incident light.

• Number of photoelectrons per second is proportional to intensity of incident radiation

The failure of classical wave theory to explain observations on photoelectricity.

• Intensity of wave (brightness of light) should determine whether photoelectron emitted/KE of photoelectron so wave theory could not explain the maximum kinetic energy of photoelectrons.

• Light of any frequency should cause emission so the wave theory could not account for the existence of the threshold frequency.

• Wave energy spread over surface should mean time needed to for electrons to accumulate enough energy to be emitted/lower intensity the longer the time could not explain the instant emission of photoelectrons.

Einstein’s explanation of photoelectricity

• Light is made of photons.

• Photoelectrons due to one photon interacting with one electron in surface of metal.

• Minimum energy (work function of metal) needed for electron to be emitted related to a threshold frequency by ϕ= hf₀

• Remaining energy of photon (hf-hf₀) becomes (max) KE of photoelectron. E=hf+ϕ+E_k(max)

• Brighter source means more photons (per second) and therefore more photoelectrons (per second).

Stopping potential

• If a potential is applied across a metal surface/ emitter plate that makes it positive this opposes the flow of the photoelectric current as the photoelectrons must do work against the electrostatic force of attraction towards the surface causing the kinetic energy of the photoelectrons will decrease.

• As this potential is increased the emitter plate becomes more positive, the number of photoelectrons with enough kinetic energy to cross the gap decreases.

• The stopping potential is the potential difference you would need to apply across the metal to stop the photoelectrons with the maximum kinetic energy.

• E_k(max)=eV_s

• E=hf+ϕ+E_k(max)

• hf=ϕ+E_k(max)=ϕ+eV_s

• V_s=(h/e)f-(ϕ/e)

• Therefore, if you plot a graph of stopping potential against frequency of light, you will get a straight line graph with a gradient of (h/e), a y-intercept of -(ϕ/e) and an x-intercept which is the threshold frequency of the metal.

• This experimental evidence confirmed Einstein’s photon theory of light.

De Broglie’s hypothesis

• The de Broglie hypothesis states that all particles have a wave-like nature and a particle nature, and that the wavelength of any particle can be found using the following equation: λ=h/mv.

• p=mv=h/λ.

Electron diffraction

• To investigate whether electrons did exhibit wave-like properties, an electron diffraction tube was produced

• The electrons were accelerated in an electron gun with a high potential difference, such as 5000 V, and were then directed through a thin film of graphite

  • The gaps between the carbon atoms were sufficiently small to cause diffraction, using the predicted DeBroglie wavelength of electrons 

  • Diffraction is a property of waves when passing through a small gap - if the electrons were seen to diffract then this was proof of their wave-like properties

• The electrons were indeed seen to diffract from the gaps between carbon atoms and produce a circular pattern on a fluorescent screen made from phosphor

λ=h/√2meV derivation for electron diffraction

• eV=1/2 mv² so v=√2eV/m

• p=mv=m(√2eV/m)=√m²(√2eV/m)=√m²2eV/m)=√2meV

• λ=h/p=h/√2meV

Effect of potential difference on the diffraction pattern

• Using λ=h/√2meV you can see that as the accelerating voltage is increased, the speed of electrons increases and so their de Broglie wavelength decreases, so the electrons are diffracted less and the fringe spacing will decrease (the rings will move closer).

• The converse is also true, as accelerating voltage is decreased, the speed of electrons decreases so their de Broglie wavelength increases, so the electrons are diffracted more and the fringe spacing will increase.

• This follows wave theory, which states the fringe spacing in a diffraction pattern will increase as wavelength increases, providing further evidence to support the de Broglie hypothesis.

Estimate of anode voltage needed to produce wavelengths of the order of the size of the atom.

• The de Broglie wavelength needs to roughly equal the diameter of the atom - roughly 0.1nm

• λ=h/√2meV

• λ√2meV = h

• √2meV = h/λ

• 2meV = (h/λ)²

• V = h²/2meλ²

• = 150V roughly

Benefits of using electron microscopes over light microscopes

The wavelength of an electron beam is much smaller than that of light, meaning electron microscopes have a much higher resolving power than light microscopes, so are used to view incredibly small structures. As the wavelength of the electrons decreases the resolving power of the microscope increases.

How does a TEM form an image

• In a TEM electrons are accelerated by an electron gun, and pass through a set of magnetic lenses, passing through an extremely thin sample so that the electrons do not slow down, and their wavelength doesn’t change.

• Electrons through the middle of the lenses are undeviated.

• Electrons at the edges of the lens are deflected by magnetic fields towards the axis of the TEM.

• Condenser lens deflects the electrons into a wide parallel beam incident uniformly on the sample.

• Objective lens will form an image of the sample.

• Projector lens then casts a second image onto the fluorescent screen.

Factors that affect the quality of, and the level of detail in, the image of the TEM.

• Wavelength depends on speed of the electrons.

• Lower the wavelength gives greater the detail.

• Emitted electrons come from a heated cathode and therefore have a speed distribution dependent on temperature.

• The speed of the electrons is not always the same which causes different pathways through the lens and so aberration.

• The sample thickness reduces the speed of the electrons increasing the wavelength and decreasing the detail.

How does an STM form an image

• An STM is formed of a very fine tipped probe, which moves across the surface of an object and stays at a constant potential (can be either negative or positive), meaning electrons can only travel in one direction.

• An STM uses quantum tunnelling of electrons in order to form an image of the surface of an object.

• Quantum tunnelling involves:

  • A potential/coulomb barrier that electrons (in surface) have to overcome.

  • Electrons have insufficient energy so (due to wave properties of electrons) there is a probability of electrons crossing from sample to tip of probe.

• The smaller the barrier/gap, the more likely it is that tunnelling will occur.

• This movement of electrons from the surface to the tip of the probe can be measured and is known as the tunnelling current.

• As the probe moves across the surface, the size of the gap will vary, when it becomes larger, tunnelling current will decrease as tunnelling of electrons is less likely to occur and when it becomes smaller, tunnelling current will increase as tunnelling of electrons is more likely.

• There are two ways an STM can operate:

  • Constant height mode

  • Constant current mode

Constant height mode

• The probe is kept at a constant height as it moves across the surface, and the tunnelling current is recorded.

• When probe moves over higher layer of electrons, current increases.

• This is used to image the surface of the object.

Constant current mode

• Tip of probe maintained a certain distance (about 1nm) above surface.

• When probe moves over higher layer of electrons, current increases.

• Through a feedback process the tip is moved higher to reduce current to original value.

• The movement of the probe can then be used to image the surface.