Unit 7

parameter

# that describes some characteristic of the population

statistic

# that describes some characteristic of a sample _{^{(taken from a sample)}}

symbols for statistics (proportion, mean, SD)

p̂, x̄, s

symbol for parameters (proportion, mean, SD)

p, μ, σ

!!! sampling variability: the value of a statistic varies in a repeated random sampling

Population must be 10x larger or more than sample (10% Condition)

NEVER ASSUME NORMALITY -> always check 10% (can find SD) and large counts condition (can use approx. Normal distribution and find probability) for sample proportion/sample mean _{^{(LCC is np ≥ 10 and n(1-p) ≥ 10 for sample proportion; n ≥ 30 for sample mean)}}

Interpret answer by using context

usually give statistic + sample, look at bigger picture to find parameter + population

p̂ = X/n (sample proportion = count of successes in sample over sample size) _{^{(proportion is the proportion of successes out of a sample. Think fraction or decimal)}}

statistic likely to be off from parameter if n is low/small

sampling distribution

the distribution of values of a statistic of all possible samples of the same size from the same pop.
_{^{^difficult to do, so a simulation is appropriate ex: 30 samples of size n
^each point is a statistic collected from a sample of the same size. take statistic from EACH SAMPLE for many many samples. shows all possible values that the statistic can take and how often it occurs}}

population distribution

gives the values (data points) of the variable for all the individuals in the pop. (data/numbers of population)

^ex: every U.S. income; the U.S. Census _{^{(info abt every citizen)}}

distribution of sample data

shows the values of the variable for all the individuals in the sample (data/numbers from sample)

^ex: the incomes from the sample of 200 Americans

unbiased estimator

a statistic used to estimate a parameter

-IF the mean of its sampling distribution equals the true value of the parameter being estimated (ex: sample mean, sample proportion_{^{, SD; NOT median}}) _{^{(aka if in many samples, the values of the statistic are centered at the value of the parameter)}}

-ex: can use x̄ if the expected value of the sampling distribution _{^{(mean of many means of many samples)}} equals μ

variability of a statistic

described by the spread of its sampling distribution

^incr sample size, decr variability/spread of distribution of statistic _{^{(decr variability in sample)}}

^larger sample -> more data/info abt population -> more precise estimates (+less variability of the sample statistic)

bias

variability

aim is off consistently

how scattered/close it is (similar results or not?)

!best estimate → want low/no bias (close to actual parameter), low variability (data close tgt & less spread out)!

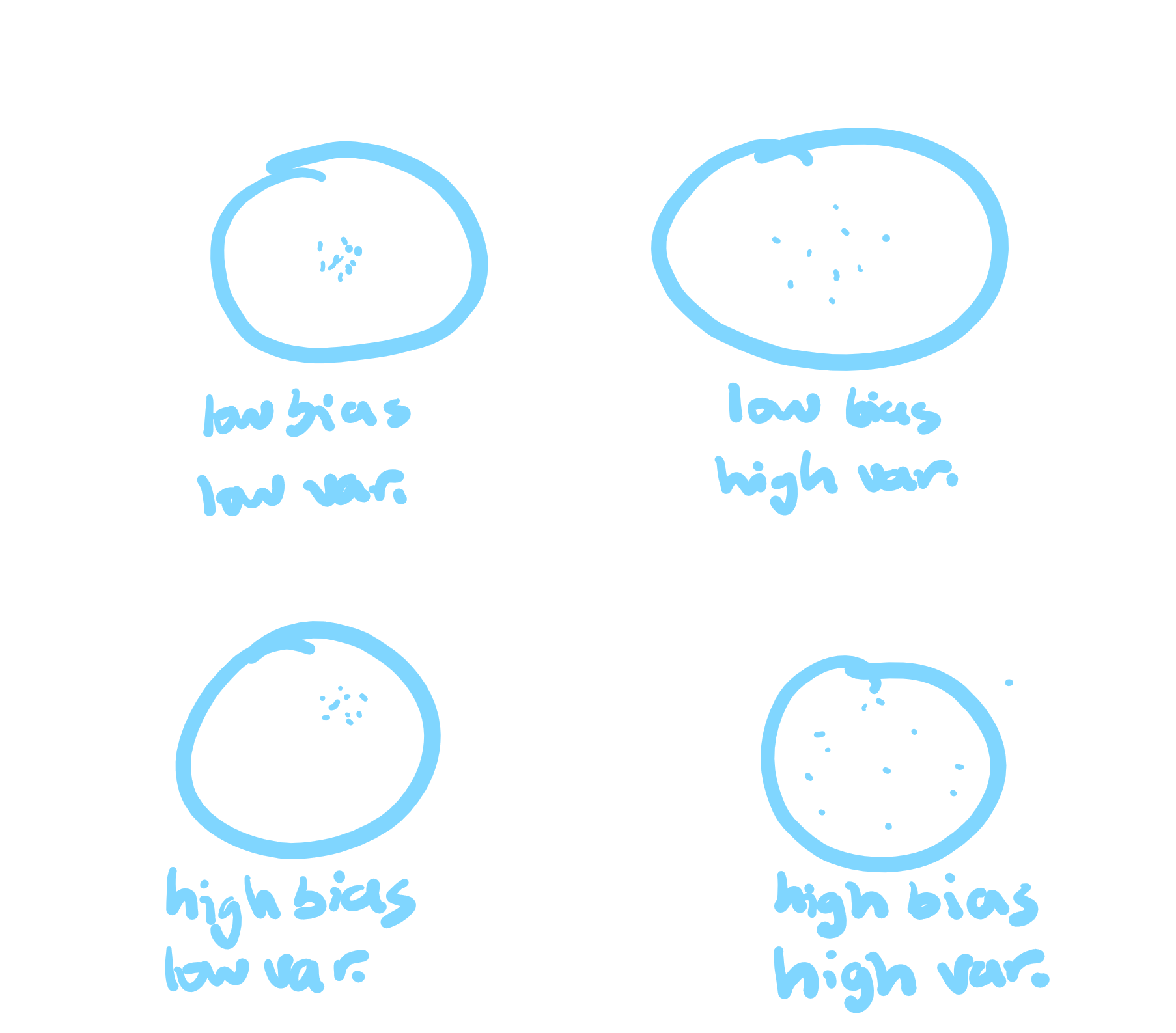
about sample proportion distributions

SHAPE: can be approx normal _{^{(depends on n sample size and p population proportion, large counts condition)}}

CENTER: μ_p̂ = p (b/c p̂ is an unbiased estimator of p)

SPREAD: incr n (sample size), decr σ_p̂ (sample spread) (σ_p̂ depends on n and p)

_{^{*n changes, variability changes (don’t look at N)}}

Sampling distribution of a sample proportion _{^{(choose SRS of size n from population size N w/ proportion p of success, let p̂ be the sample proportion of successes)}}

μ_p̂ = p

10% condition before find SD → n ≤ 1/10*N (use words if given n but not N (can assume N is large))

σ_p̂ = √ [p(1-p)/n]

check large counts condition: np ≥ 10 and n(1-p) ≥ 10 → then can find probability and use normal curve shape

*state the # of ppl needed to assume the SD
_{^{^as n incr, sampling distrib. becomes approx normal}}

as n changes, what happens to shape, center, and spread? _{^{(for sample proportion & sample mean)}}

shape approx same (normal) _{^{(decr n slightly less normal, incr n appears to look more normal)}}

same center

SD changes

• incr n, decr SD

• decr n, incr SD

• SAMPLE PROPORTION: find factor from OG size n to final size n _{^{(ex: times 1/6)}}. the factor that SD changes by is the reciprocal of that then sqr root. (ex: 1/6 → √6)

• SAMPLE MEAN: find factor from OG size n to final size n _{^{(ex: times 2)}}. the factor that SD changes by is 1 over the sqr root of the OG factor (ex: 2 → 1/√2)

!!! ask for parameters/statistics -> make sure to give #s and use symbols! ^parameter from population, statistics from sample

avoid absolutes (prob wrong if says 'exactly Normal')

good estimator → see if sampling distrib. mean of the statistic matches parameter _{^{(ex: sampling distrib. mean of mean temperatures matches parameter mean temp.)}}
^what is it centered around?
^find mean by adding all values _{^{(ticks, make sure to include if multiple of the same #)}} then dividing by the # of dots
^n is the sample size!!!

-

SAMPLING DISTRIB OF MEAN

-SD will decr if sample size incr

-SD is a measure of the variability of the sample mean among repeated samples

-sample mean is an unbiased estimator of the true population mean (also, sample proportion is unbiased estimator of the true population proportion)

-sampling distribution show how the sample mean will vary in repeated samples

Sampling distribution of a sample mean _{^{(suppose x̄ is the mean of an SRS of size n drawn from a large population with mean μ and SD σ)}}

μ_x̄ = μ

10% condition before find SD → n ≤ 1/10*N (use words if given n but not N (can assume N is large)) _{^{(overlook independence violation)a}}

σ_x̄ = σ/√n

if shape of population distribution is normal, then shape of sampling distribution of x̄ is also normal (no matter the size of n) → can find probability

if shape of pop. distrib. is NOT normal, then shape of sampling distribution of x̄ is normal if n ≥ 30 → can find probability

central limit theorem

when n is large (n ≥ 30), sampling distribution of the sample mean x̄ is approx normal

^no matter the shape of the population distribution (even if shape is not normal!)

*incr n, incr shape look normal _{^{(think incr n, decr SD, data closer tgt and more centered)}}

_{^{*given population has a finite SD}}