Chapter 2: Kinematics

\

Average and Instantaneous Motion

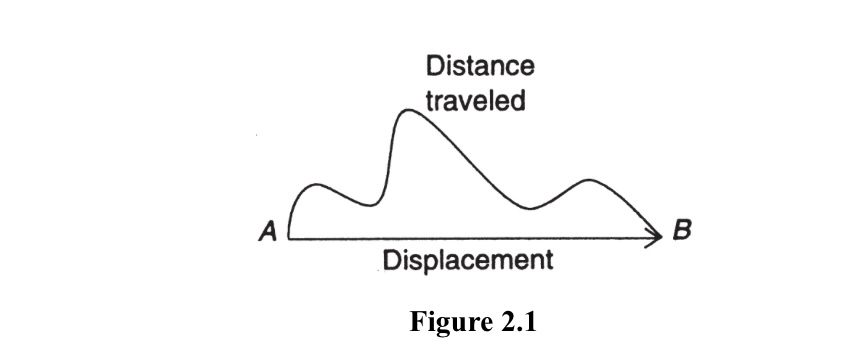
• Average motion is defined as the total displacement of an object divided by the time it takes for that displacement to occur. This means that the average motion of an object is the overall change in position during a certain period of time.
• Instantaneous motion is defined as the motion of an object at a specific point in time. This means that instantaneous motion gives us information about an object's position, velocity, and acceleration at a particular moment.
• Average velocity is defined as the change in displacement divided by the time interval over which the change occurs. It is a vector quantity that specifies both the speed and direction of an object's motion.
• Instantaneous velocity is defined as the limit of the average velocity as the time interval approaches zero. This means that it is the velocity of an object at a specific instant in time.
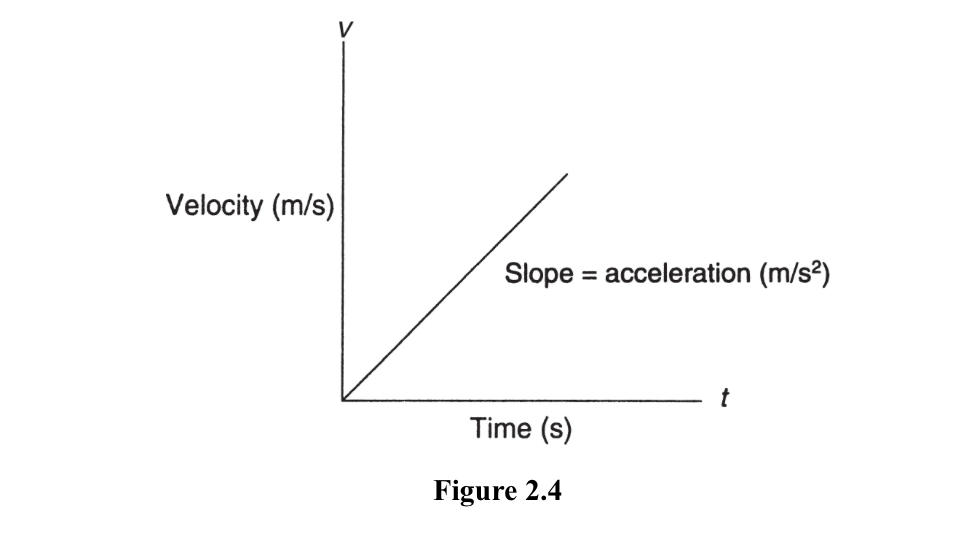
• Acceleration is defined as the rate of change of velocity. It is a vector quantity that specifies both the magnitude and direction of a change in velocity.
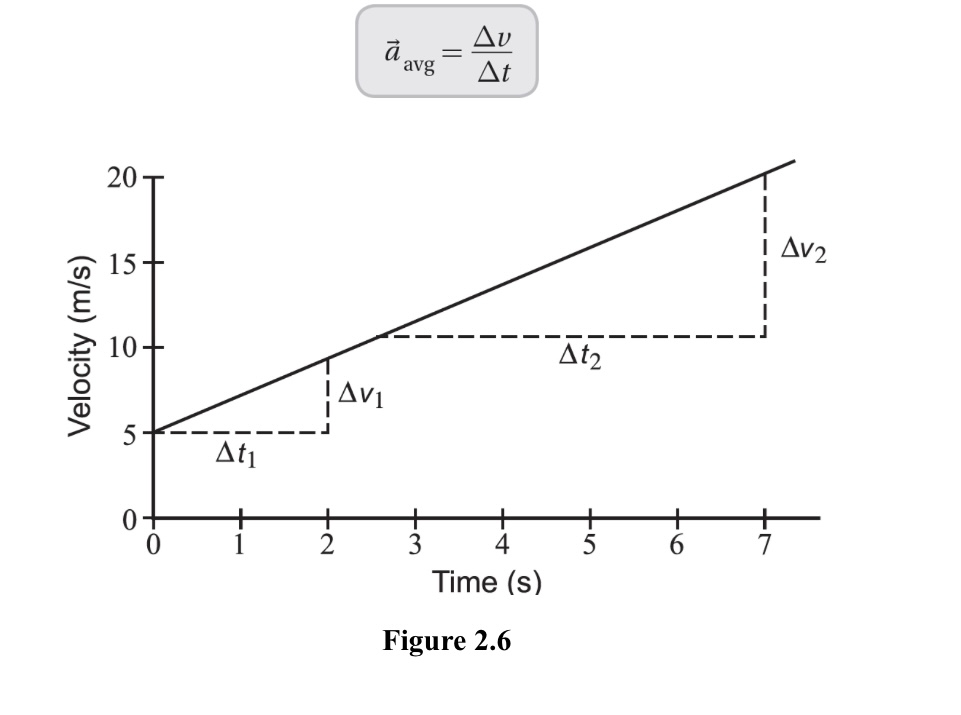
• Average acceleration is defined as the change in velocity divided by the time interval over which the change occurs. It is a vector quantity that specifies the average rate of change in velocity over a certain period of time.
• Instantaneous acceleration is defined as the limit of the average acceleration as the time interval approaches zero. This means that it is the acceleration of an object at a specific instant in time.
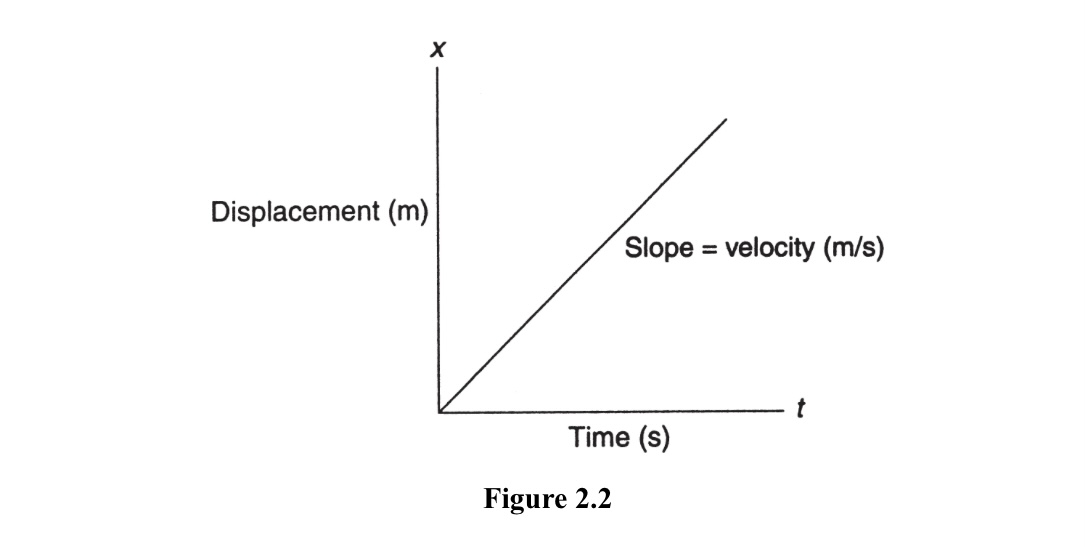
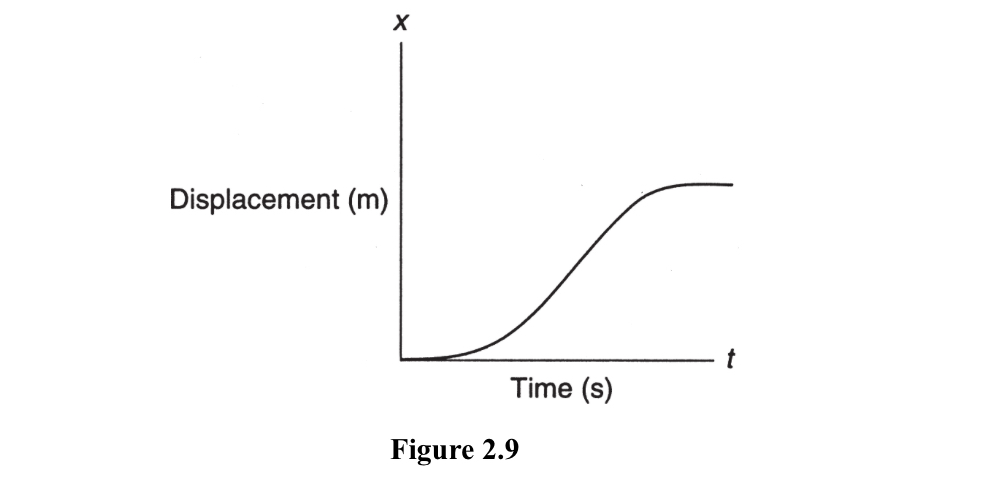
• Graphs can be used to represent both average and instantaneous motion. For example, a position-time graph can be used to show an object's average velocity, while a velocity-time graph can be used to show an object's average acceleration. A tangent to the curve of a position-time graph at a specific point gives the instantaneous velocity at that point, while a tangent to the curve of a velocity-time graph at a specific point gives the instantaneous acceleration at that point.

\
Average and Instantaneous Motion

\

TIP:

Speed is a scalar quantity while velocity is a vector quantity.

Sample Problem

A projectile is fired vertically upward at an initial velocity of +98 m/s.

How high will it rise? How long will it take the projectile to reach that height?

Solution

We use a =-9.8 m/s^2 (Recall gravity's direction is downward) and note that vp = 0 at the highest point:

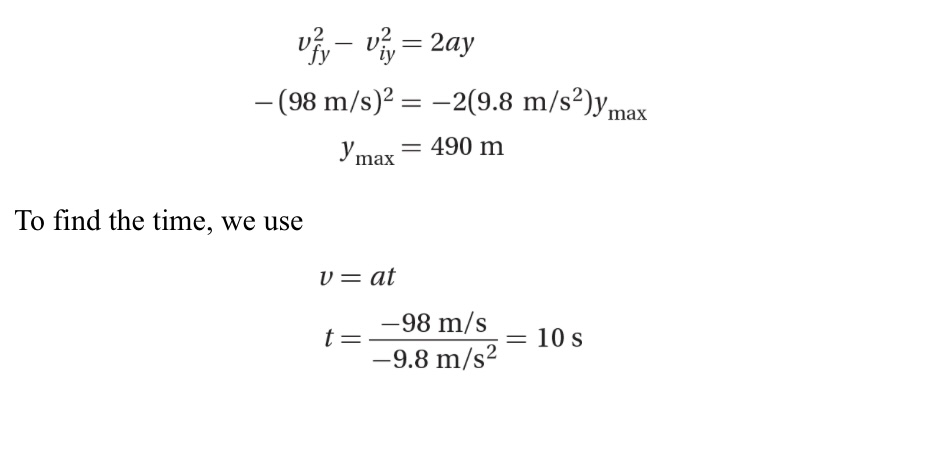
Acceleration

• Acceleration is the rate at which an object's velocity changes over time and is measured in meters per second squared (m/s^2).

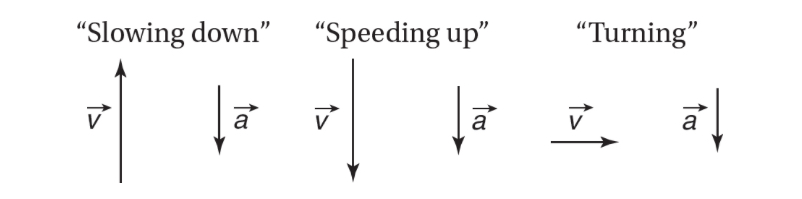
• Acceleration can be positive, negative, or zero. Positive acceleration occurs when an object's velocity is increasing in the positive direction, negative acceleration occurs when an object's velocity is decreasing in the positive direction, and zero acceleration occurs when an object's velocity is constant. \n

  TIP:

  Acceleration is a vector quantity equal to the rate of change of velocity.

  \

• The relationship between acceleration, velocity, and time is described by the equation a = (vf - vi) / t, where a is acceleration, vf is the final velocity, v_i is the initial velocity, and t is the time interval.

• Acceleration is related to the net force acting on an object through Newton's second law, which states that the net force on an object is equal to its mass times its acceleration (F_net = ma).

• When an object is in free fall near the surface of the Earth, it experiences a constant acceleration of approximately 9.8 m/s^2 due to the force of gravity.

• The acceleration of an object moving in a circular path is related to its velocity and the radius of the circle through the equation a = v^2 / r, where a is acceleration, v is velocity, and r is the radius of the circle.

• The concept of centripetal acceleration is used to describe the acceleration of an object moving in a circular path toward the center of the circle and is given by the equation ac = v^2 / r.

• Acceleration is a key concept in kinematics, which is the branch of physics that studies the motion of objects without considering the forces that cause the motion. It is also important in other areas of physics, such as dynamics, which studies the forces that cause motion.

  \
  \
  

  

Graphical Analysis of Motion

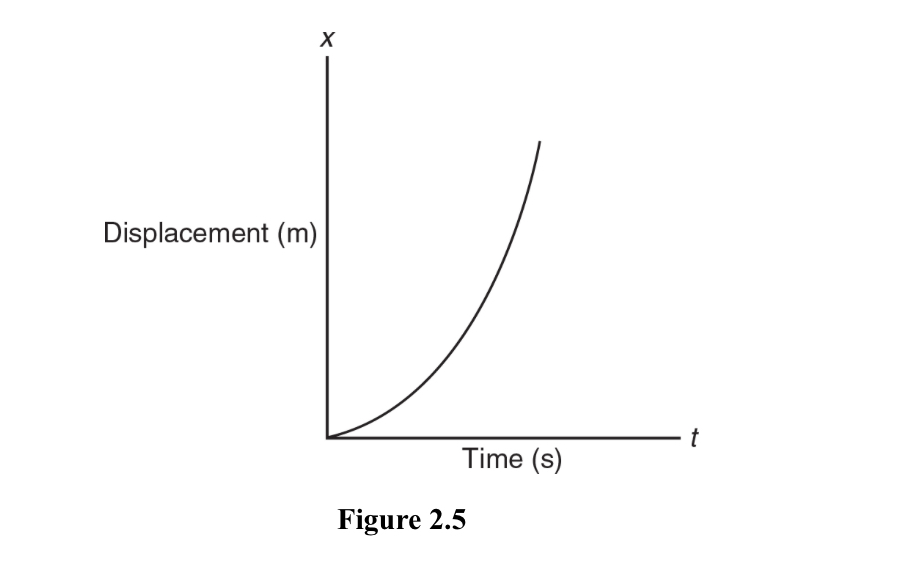
• Position-time graphs are used to analyze motion in one dimension. The slope of the tangent line at any point on the graph gives the instantaneous velocity at that point, and the area under the curve gives the displacement over a given time interval.
• Velocity-time graphs are used to analyze acceleration in one dimension. The slope of the tangent line at any point on the graph gives the instantaneous acceleration at that point, and the area under the curve gives the displacement over a given time interval.
• Acceleration-time graphs are used to analyze jerk, which is the rate of change of acceleration over time. The slope of the tangent line at any point on the graph gives the instantaneous jerk at that point, and the area under the curve gives the change in acceleration over a given time interval.
• Displacement-time graphs are used to analyze motion in two or three dimensions. The slope of the tangent line at any point on the graph gives the instantaneous velocity at that point, and the area under the curve gives the displacement over a given time interval
• Velocity-time graphs are used to analyze motion in two or three dimensions as well. The slope of the tangent line at any point on the graph gives the instantaneous acceleration at that point, and the area under the curve gives the change in velocity over a given time interval.
• The slope of a position-time graph gives the average velocity over a given time interval, while the slope of a velocity-time graph gives the average acceleration over a given time interval.

\

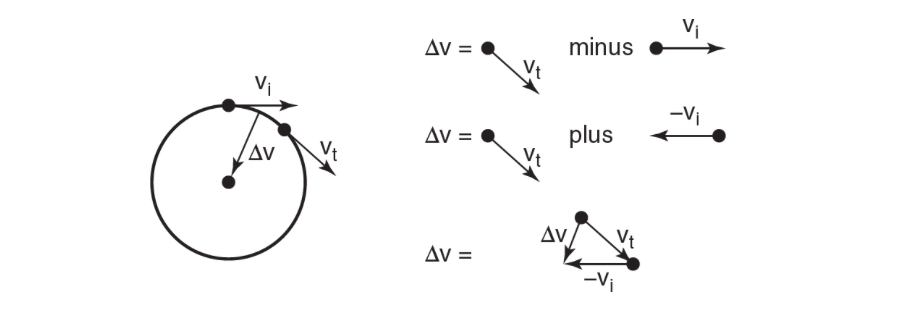
Relative Motion

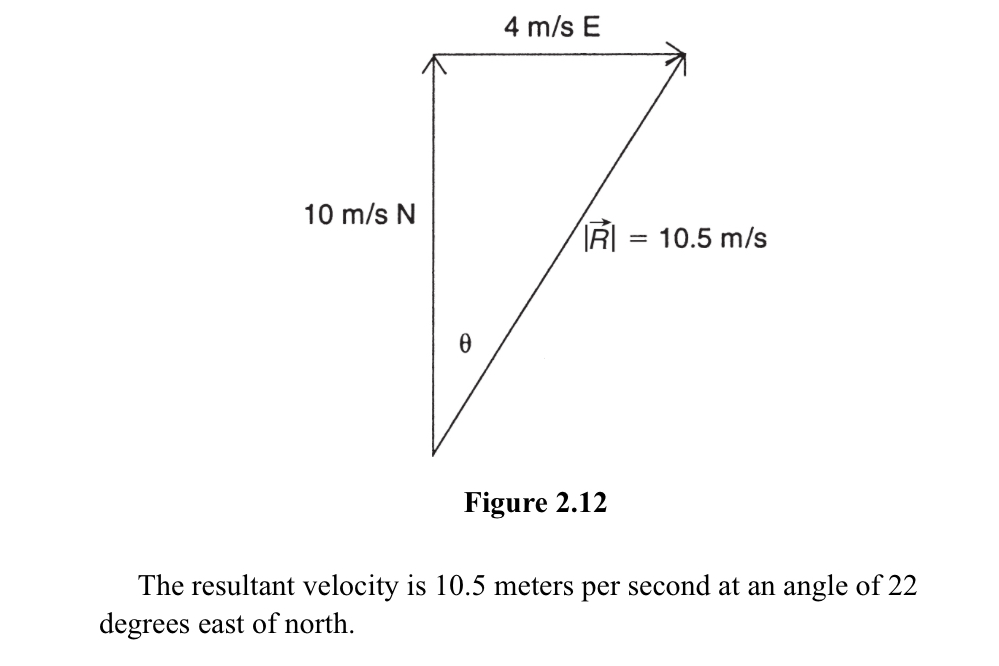
• Relative motion is the study of the motion of an object with respect to another object or a reference frame.
• Motion is always relative to a reference point, which is a point that is used to determine the position of an object in space.
• The velocity of an object is always relative to the velocity of another object or a reference frame.
• The direction of motion of an object is determined by the relative position of the object and the reference frame.
• The distance traveled by an object is determined by the displacement of the object relative to a reference frame.
• The acceleration of an object is always relative to the acceleration of another object or a reference frame.
• Relative motion can be used to analyze the motion of objects in different reference frames, which can be useful in situations where the observer is moving, or the object is moving.
• The concept of relative motion is fundamental to the understanding of concepts such as kinematics, dynamics, and energy, and is essential in the study of mechanics.

\

Horizontally Launched projectiles

• A horizontally launched projectile is an object that is launched horizontally with an initial velocity and moves in a projectile motion under the influence of gravity.

• The initial horizontal velocity of the projectile remains constant throughout its motion, while its vertical velocity changes due to the effect of gravity. \n

  

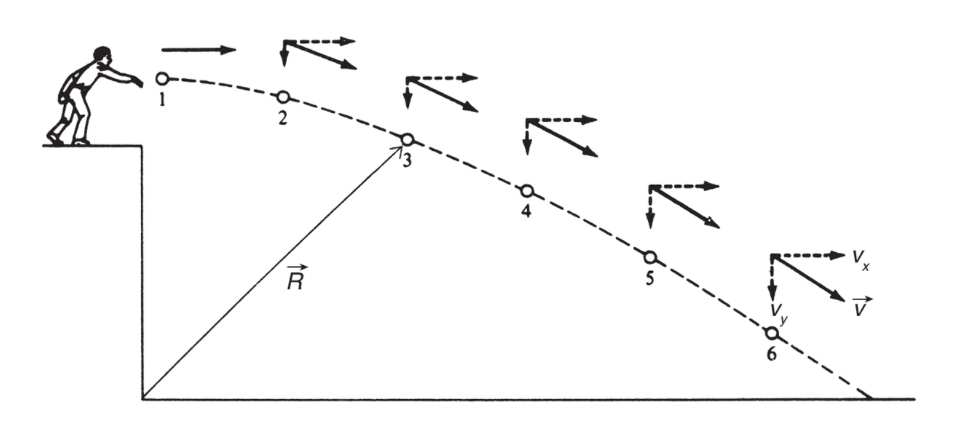
• The horizontal and vertical components of the motion are independent of each other, meaning that the motion in the horizontal direction does not affect the motion in the vertical direction, and vice versa.

• The trajectory of a horizontally launched projectile is a parabolic path, with the maximum height achieved at the halfway point of its flight.

• The time of flight of a horizontally launched projectile is determined solely by its vertical motion and is given by the equation t = 2v₀/g, where t is the time of flight, v₀ is the initial vertical velocity, and g is the acceleration due to gravity.

• The horizontal range of a horizontally launched projectile is determined by its initial horizontal velocity and the time of flight and is given by the equation R = v₀x × t, where R is the range, v₀x is the initial horizontal velocity, and t is the time of flight.

• The velocity vector of a horizontally launched projectile changes direction continuously due to the effect of gravity, but its magnitude remains constant in the absence of air resistance.

• The motion of a horizontally launched projectile can be analyzed using vector components and the kinematic equations of motion, including the equations for displacement, velocity, acceleration, and time.

REMEMBER

For all projectiles, the two-component motions are independent of each other. The horizontal velocity remains constant throughout the projectile's motion.

\

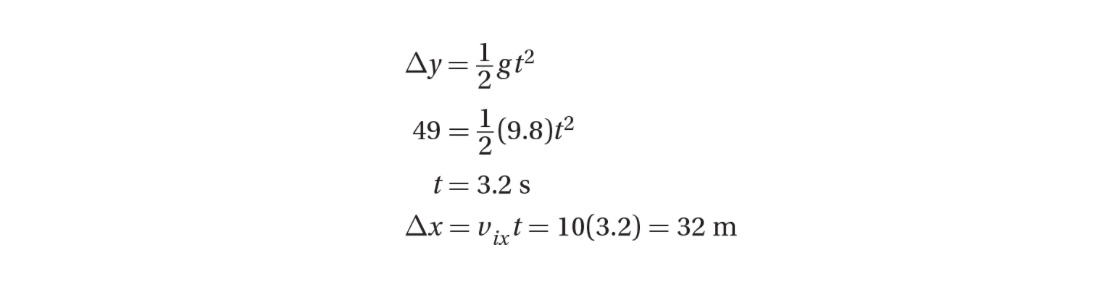
Sample Problem

A projectile is launched horizontally from a height of 25 m, and it is observed to land 50 m from the base. What was the launch velocity?

Solution

We know that vertical motion is independent of horizontal motion. Thus, we can find the time that the projectile is in the air using:

\

Sample Problem

A projectile is launched from the ground at a 40° angle with a velocity of 150 m/s. Calculate the maximum height of the projectile.

Solution

From trigonometry, we know that vi = Vo sin 0. Thus,

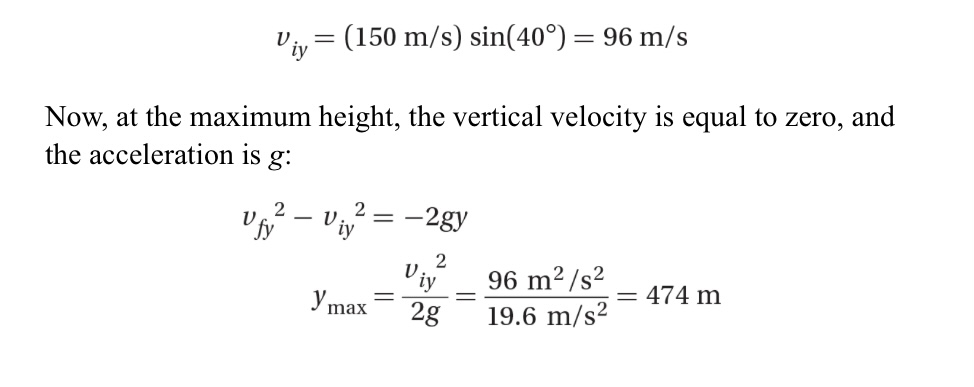
Projectiles launched at an angle

• A projectile launched at an angle has both horizontal and vertical components of velocity, which are determined by the initial velocity and launch angle.
• The initial velocity of a projectile launched at an angle can be resolved into horizontal and vertical components using trigonometry.
• The vertical component of velocity determines the height and time of flight of the projectile, while the horizontal component of velocity determines the range of the projectile.
• The trajectory of a projectile launched at an angle is a parabolic path, with the maximum height achieved at the apex of its flight.
• The time of flight of a projectile launched at an angle can be determined using the equation t = (2v₀sinθ)/g, where t is the time of flight, v₀ is the initial velocity, θ is the launch angle, g is the acceleration due to gravity.
• The range of a projectile launched at an angle can be determined using the equation R = (v₀²sin(2θ))/g, where R is the range, v₀ is the initial velocity, θ is the launch angle, and g is the acceleration due to gravity
• The velocity vector of a projectile launched at an angle changes direction continuously due to the effect of gravity, but its magnitude remains constant in the absence of air resistance.
• The motion of a projectile launched at an angle can be analyzed using vector components and the kinematic equations of motion, including the equations for displacement, velocity, acceleration, and time.

Uniform Circular Motion

• Uniform circular motion is the motion of an object moving at a constant speed in a circular path. The velocity of the object is constantly changing because its direction is changing, but the magnitude of the velocity remains constant.

• Centripetal force is the force that keeps an object moving in a circular path. It is directed towards the center of the circle and is proportional to the square of the velocity of the object and inversely proportional to the radius of the circle.

  \
  

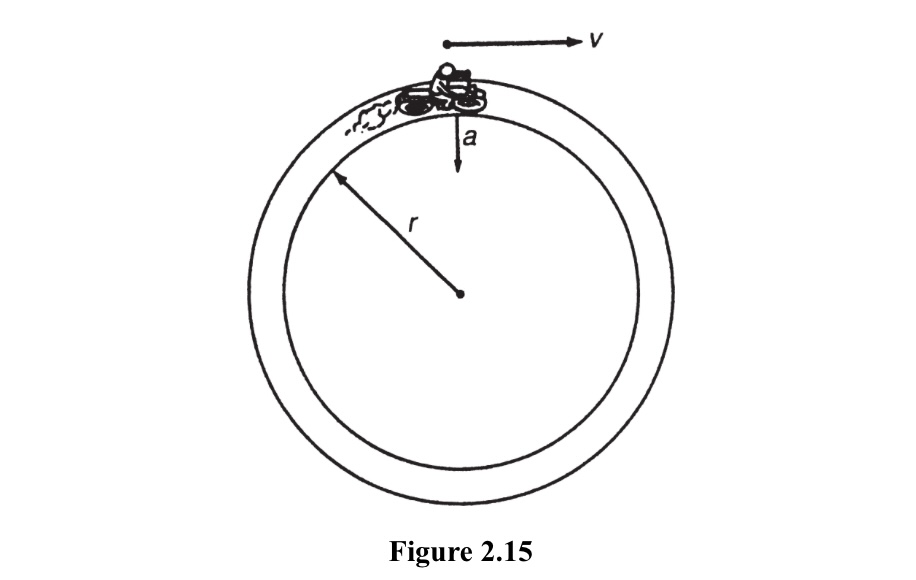
  The direction of the acceleration is toward the center and is called the centripetal acceleration. The magnitude of the centripetal acceleration is given by two formulas:

  

Recalling that the circumference of a circle is Zar, the speed must be:

• The period of a circular motion is the time it takes for an object to complete one full revolution around the circle. It is related to the frequency of the motion by the equation: T = 1/f, where T is the period and f is the frequency.

• The centripetal acceleration of an object in uniform circular motion is given by the equation: a = v^2/r, where a is the centripetal acceleration, v is the velocity of the object, and r is the radius of the circle.

• The tangential velocity of an object in uniform circular motion is given by the equation: v = 2πr/T, where v is the tangential velocity, r is the radius of the circle, and T is the period of the motion.

  \
  Sample Problem:

  A 5-kg mass is undergoing uniform circular motion with a constant speed of 10 m/s in a circle of radius 2 m. Calculate the centripetal acceleration of the mass.

  Solution:

  We use the formula:

  \
  

  \
  \
  \
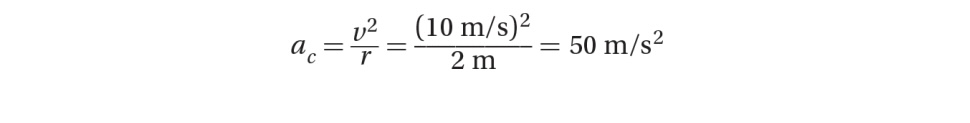
  \n \n \n \n \n \n \n \n \n

\