Stats 200 midterm

Categorical variable

represent types of data which may be divided into groups

Quantitative Variable

outcomes can be measured on a numerical scale

what can you use to show Categorical data

1. freqeuncy tables

2. contingency tables

3. marginal distributions 

4. conditional distrbutions graphical displays 

   1. bar charts 

   2. pie charts 

Frequency (relative) tables 

displays all categories of a single categorical variable with associated (relative) frequences 

Contingency tables

Used to display the relationship between two categorical variables, showing the frequency counts for each combination of categories.

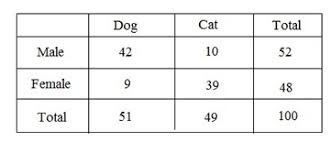
marginal distributions

displaying distribution of one of the two variables only

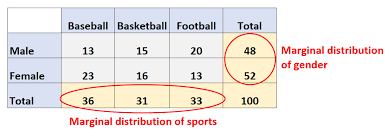
Conditional distributions

displaying distribution of one variable satisfying a condition of another variable

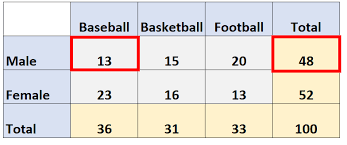
why can’t you compare counts on a table but instead %?

counts aren’t normalized but percentages are

bar charts

used to show categorical data

pie charts

• used to show categorical data

• is a good choice when you want to show that one variable is more or less frequent than the others 

simpson’s paradox

a statistical phenomenon where a trend that appears in different groups of data disappears or even reverses when the groups are combined

what can you use to show Quantitative data

• graphical displays 

  • histograms 

  • stem and lead displays 

  • boxplots 

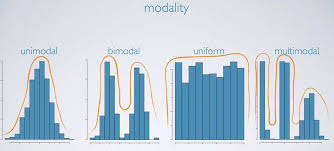
modality of histrograms

number of peaks:

• unimodel

• bimodel

• multimodel

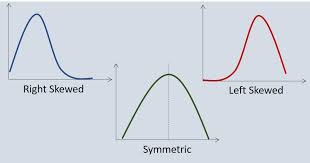
Symmetry of histograms

1. symmteric

2. skewed to the right (with a long right tail)

3. skewed to the left (with long left tail)

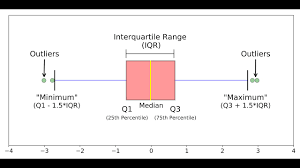
boxplot parts 

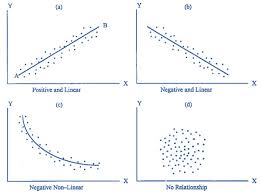
scatterplots

• helps visualize possible relationships between 2 quantitative variables 

Types of scatterplots: 

• Direction: 

  • Positive

  • Negative 

• Form: 

  • Linear 

  • Non-linear 

• How scattered are the points? 

  • Strong 

  • Weak or no relationships (when data is randomly scattered)

• Outliers?

What is ploted on x and y axis of scatter plot

• Explanatory variable should be plotted on the x-axis 

• Response variable should be plotted on the y-axis 

Correlation and types

• The degree of linear association between 2 quantitative variables 

• Positive correlation: 

  • Large values of x’s are linearly associated with large values of y 

• Negative correlation: 

  • Large values of x are linearly associated with small values of y

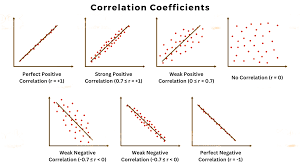
Correlation coefficient (r ):

• A measure of strength of a linear association between 2 quantitative variables 

Properties of the Correlation coefficient r:

1. If the two variables are positively correlated, r will be positive 

2. If the two variables are negatively correlated r will be negative 

3. R has a alue between -1 and 1 inclusive; and have no units 

4. R = -1 for perfect negative correlation 

5. r= +1 for perfect positive correlation 

6. R close to 0 implies a weak or no linear relationship between the 2 variables

7. As the degree of positive correlation increases, r becomes closer to 1

8. As degree of negative correlation decreases, r becomes closer to -1. 

9. Swapping x and y variables does not affect the value of r 

10. The value of r does not change if all values of either variable are added a constant or multiplied by a positive constant 

11. R is sensitive to outliers, so it may not be a reliable measure of strength of a linear relationship when there are outliersIf the two variables are positively correlated, r will be positive 

Lurking variable

a third variable that associates with both x and y 

Regression line

• the relationship between two variables x and y

• The line will pass through the mean-mean point 

Residuals

is defined as the difference between the observed value y and the predicted value y hat. 

• The sum of residuals is equal to zero 

• The linear model, also called the least squares regression line, is obtained by minimising the sum of the squared residuals 

Residual plot

• plots the residuals against the data of the explanatory variable, if the model is appropriate, the residual plot should show no pattern. 

Always keep outliers unless

• 1. Entries errors 

• 2. Don’t fit the population you are looking at

Influential points

data points that greatly change the regression model, so they are removed. 

Extrapolation

refers to the prediction about a response variable y for values of an explanatory variable x that lies outside the observed range, once you leave the range the relationship you observed may not hold anymore so the data may not be accurate, so DO NOT EXTRAPOLATE

Population

the complete collection of individuals under a study

Census

provides a means to obtain complete and accurate information about a population interest → sometimes is impossible because your population is too big, so a sample is taken instead 

Sample

a subset of individual selected from a population, can provide relabile information about the population but it will be biased. 

Bias

 means that is has errors since the sample isn’t represented well. 

Parameter

refers to a numerical summary of a population. 

Statistic

amount/number you get from a sample. 

Things that matter when making a sample

1. Randomization

   1. Usually gives samples that have similar characteristics to a population

2. Sample size 

   1. A large size is better but the sample should also be representative else it is a bad sample no matter what 

Sampling Frame

the list of individuals from which the sample is drawn. One must define clearly what or who the population is to include. 

Sampling variability

 the difference in characteristics from sample to sample

sampling methods

1. Simple random sampling (SRS)

   1. N individuals sampled at random from a population 

   2. Each individual has an equal chance of being picked

   3. Has a lot of variability

2. Stratified sampling 

   1. First the population is divided into a strata, then a simple random sample is drawn within each strata

   2. Has smaller variability, so the results are more reliable 

   3. Makes sure each group is proportionally represented. 

   4. Proportional allocation: the size of SRS is proportional to the size of the stratum in the population. 

3. Clutter sampling 

   1. Divides the population into different clusters and a simple random samples from certain clusters 

   2. Used for convenience, practicality, and cost-efficiency 

4. Multistage sampling 

   1. Involves one or more stages of sampling procedure to get a sample 

   2. Ex. 2 stage cluster sampling 

5. Systematic sampling 

   1. Selects every kth individual from a sampling frame 

   2. Should not contain any hidden order

Biases in sampling

1. Undercoverage 

   1. When a sampling procedure completely excludes or underrepresents a certain kind of individual from the population. 

2. Convenience sampling 

   1. Uses a convenient way of sampling for you to get a sample but its not a good sample. 

3. Voluntary response bias

   1. If the participation is voluntary, then the individuals who respond usually have stronger opinions than those who do not. 

4. Nonresponse bias 

   1. People who don’t respond to a survey may have different opinions than those who do. 

   2. Ex. those who work during the day may not be able to answer a phone call survey. 

5. Response bias 

   1. A subject’s response is influenced by how a question or phrase is asked. 

Observational study

two variables whole association is to be examined; has not deliberate human intervention 

Control group

baseline group for comparison

Retrospective study

data that we are collecting has already happened

Prospective study

collecting data over a period of time while classes are on going 

experiment different from observational study, since there is planned intervention (the researcher can manipulate the variables) 

Confounding variable

One variable doesn’t cause the other, but is known

Random treatment assignment

a study subject tends to balance the different treatment groups with respect to all variables expect the condition of exposure

Factor

the effect of an explanatory variable 

Levels of a factor

refers to a particular value or category of the factor. 

Principles of experimental design

1. Randomize: 

   1. Helps ‘average out’ the effects of extraneous variables that may be present 

   2. Experimental units are not always selected at random which may be a limitation 

2. Replicate: 

   1. The comparison between different treatment groups will not be reliable unless we look at moe individuals receiving each treatment

   2. One replicate may happen in another setting with a different group of individuals

3. Blocking 

   1. Controlling variables that are not factors but can effect the results 

   2. Ex. blocking an experiment by dividing individuals by male and female 

      1. Gender is the blocking variable