Theorems 1-18

Geometry theorems 1-18 **EXTRA NOTES** Use Multiplication Property when segments and angles are greater than the given ones. Use Division Property when segments and angles are less than the given ones.

Theorem 1

If two angles are right angles, then they are congruent

Theorem 2

If two angles are straight angles, then they are congruent

Theorem 3

If a conditional statement is true, then the contrapositive of the statement is also true

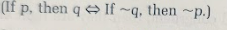
Theorem 4

If angles are supplementary to the same angle, then they are congruent

Theorem 5

If angles are supplementary to congruent angles, then they are congruent

Theorem 6

If angles are complementary to the same angle, then they are congruent

Theorem 7

If angles are complementary to congruent angles, then they are congruent

Theorem 8

If a segment is added to two congruent segments, the sums are congruent (Addition Property)

Theorem 9

If an angle is added to two congruent angles, the sums are congruent (Addition Property)

Theorem 10

If congruent segments are added to congruent segments, the sums are congruent (Addition Property)

Theorem 11

If congruent angles are added to congruent angles, the sums are congruent (Addition Property)

Theorem 12

If a segment or angle is subtracted from congruent segments or angles, the differences are congruent (Subtraction Property)

Theorem 13

If congruent segments or angles are subtracted from congruent segments or angles, the differences are congruent (Subtraction Property)

Theorem 14

If segments or angles are congruent, their like multiples are congruent (Multiplication Property)

Theorem 15

If segments or angles are congruent, their like divisions are congruent (Division Property)

Theorem 16

If angles or segments are congruent to the same angle or segment, they are congruent to each other (Transitive Property)

Theorem 17

If angles or segments are congruent to congruent angles or segments, they are congruent to each other (Transitive Property)

Theorem 18

Vertical angles are congruent