Theorems: Geometry

Corresponding angle

theyre congruent

Transitive property

a=b b=c, so a=a

Perpendicular transversal

if line is perpendicular to 1/2 parallel lines; perpendicular to other 1/2

same-side interior angle

theyre supplementary

angle addition postulate

if ray is drawn from a pt inside angle; sum of 2 angles=og angle

slope form

ax+by=c

point slope

y - y1 = m(x - x1)

distance formula

d = √[( x₂ - x₁)² + (y₂ - y₁)²]

pythag theorem

a2+b2=c2

midpt form

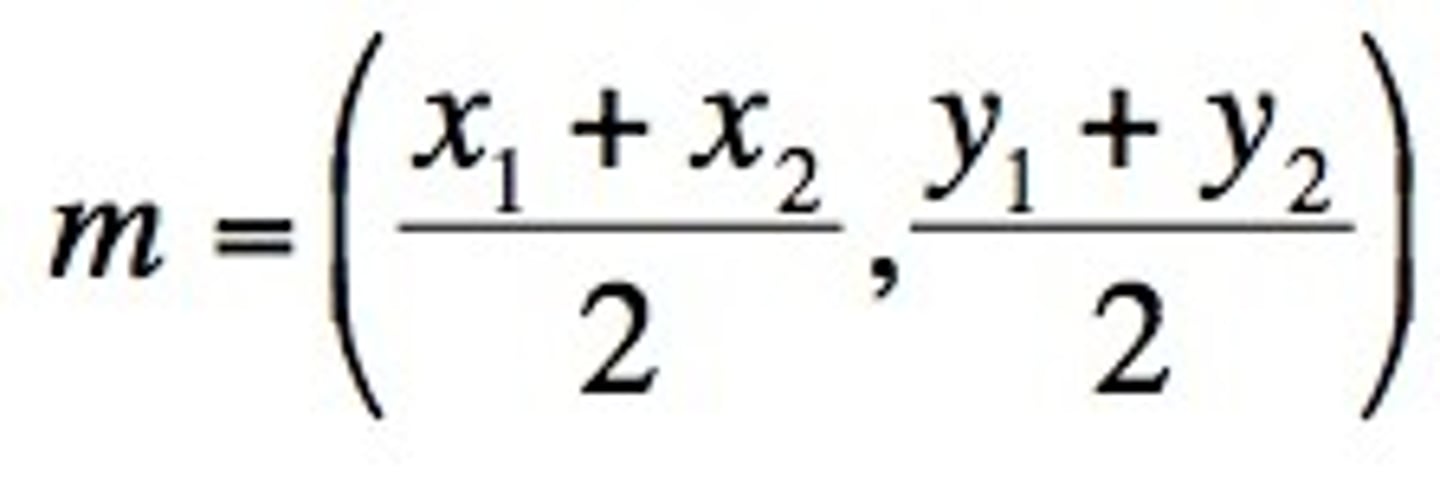
270 c

-y,x

180 c/cc

-x,-y

90 c

y,-x

rx axis

x,-y

ry axis

-x,y

ry=x

y,x

reflexive property

a line is equal to itself

cpctc

corresponding parts of congruent triangles are congruent

HL Congruence Theorem

if u have 2 ri tri and hypot and 1 leg is cong, triangles r congruent

parallelogram-rectangle

if a parallelogram has = diagonals its a rectangle

ri tri similarity

altitude drawn from hyp to ri angle then two formed and og tri are similar

arc length in degrees

θ/180 * πr

arc length in radians

θr

Arc measurement

=central angle measurement

area of tri w out height

1/2ab sin (c)

area of sector in degrees

θ/360 x πr^2

area of sector in radians

θr²/2

chord chord prod theorem

if two chords interesects, products of both chords r congruent

axb=cxd

Circle Formula

( x - h )^2 + ( y - k )^2 = r^2

What is center in circle formula

H,k

Formula to find c in quadratics

(B/2)⬆2

Right triangle diameter theorem

If a right triangle is drawn on circle, the hypotenuse is the diameter

Inscribed quadrilateral opposite angle theorem

If quadrilateral is inscribed in circle, opposite angles r supplementary (NOT =)

Secant tangent +inscribed angle

Ad⬆2=bc

Inscribed angle

Half of central angle

Right triangle similarity theorem

if an altitude is drawn from the right angle of a right triangle to its hypotenuse, the two resulting triangles are similar to the original and to each other

Sin (90 - Θ)=

CosΘ

Cos (90-Θ)=

Sin Θ

Circle equation formula

(X-h)⬆2+ (y-k)⬆2 = r⬆2

chord chord theorem

If two chords intersect in a circle, then the products of the lengths of the chords segments are equal.

A•b=c•d

secant secant theorem

if two secants are drawn from an external point to a circle, the product of one secant's external part and its entire length equals the product of the other secant's external part and its entire length

Whole•external=whole•external

Secant tangent theorem

When a line tangent to the circle and a line secant to the circle intersect, two segments are created outside of the circle whose endpoints are the intersection point between the lines

Ad(external)↖2=bc(internal)

Inscribed angle

inscribed is ½ central angle (two chords intersect)

Right triangle diameter theorem

If right triangle is drawn in circle then hypotenuse is diameter

Inscribed quadrilateral opposite angle theorem

If quadrilateral is inscribed in circle opposite angles are supplementary

Perpendicular chord theorem

a line passing through a circle's center and perpendicular to a chord will bisect the chord