MC Gd 10 3.4 Practice blooket

Geometry / Algebra 2 (△ - Triangle)

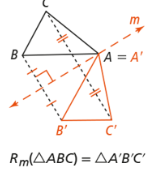
What type of rigid motion is this?

a). Reflection

b). Translation

c). Rotation

d). Guide reflection.

d). Reflection (flipping over a line)

2. The coordinates for △ABC are A(-1,2), B(2,0), and C(2,5). Reflect this from

△ABC to △A'B'C' (Rₓ-axis).

a.) The reflection coordinates from △ABC to △A'B'C' is A(-1,-2), B(-2,0), and C(-2,-5).

b.) The reflection coordinates from △ABC to △A'B'C' is A(1,2), B(2,0), and C(2,5).

c.) The reflection coordinates from △ABC to △A'B'C' is A(-1,-2), B(2,0), and C(2,-5).

d.) The reflection coordinates from △ABC to △A'B'C' is A(1,-2), B(-2,0), and C(-2,5)

Looking at your options:

c.) The reflection coordinates from △ABC to △A'B'C' is A(-1,-2), B(2,0), and C(2,-5).

This is the correct answer.

The coordinates for △ABC are A(-5,2), B(10,0), and C(5,5). Reflect this from

△ABC to △A'B'C' (Rₓ-axis).

a.) The coordinates for △ABC are A(-5,-2), B(-10,0), and C(-5,-5). Reflect this from △ABC to △A'B'C' (Rₓ-axis).

b.) The coordinates for △ABC are A(5,2), B(10,0), and C(5,5). Reflect this from △ABC to △A'B'C' (Rₓ-axis).

c.) The coordinates for △ABC are A(-5,-2), B(10,0), and C(5,-5). Reflect this from △ABC to △A'B'C' (Rₓ-axis).

d.) 2. The coordinates for △ABC are A(-5,2), B(-10,0), and C(-5,5). Reflect this from △ABC to △A'B'C' (Rₓ-axis).

Original points:

• A(-5, 2) → A'(-5, -2)

• B(10, 0) → B'(10, 0)

• C(5, 5) → C'(5, -5)

The correct option is:

c.) The coordinates for △ABC are A(-5, -2), B(10, 0), and C(5, -5).

That is a correct answer.

The coordinates for △ABC are A(1,2), B(1,3), and C(1,5). Translate 1 unit up

from △ABC to △A'B'C'.

a. The coordinates from △ABC to △A'B'C' is A(1,5), B(1,2), and C(1,7).

b. The coordinates from △ABC to △A'B'C' is A(1,3), B(1,4), and C(1,5).

c. The coordinates from △ABC to △A'B'C' is A(1,3), B(1,4), and C(1,6).

d. The coordinates from △ABC to △A'B'C' is A(1,5), B(1,7), and C(1,9).

Let’s do this for each point:

• A(1,2) → A'(1, 2+1) = A'(1,3)

• B(1,3) → B'(1, 3+1) = B'(1,4)

• C(1,5) → C'(1, 5+1) = C'(1,6)

So the correct coordinates are A'(1,3), B'(1,4), and C'(1,6).

This matches option c.

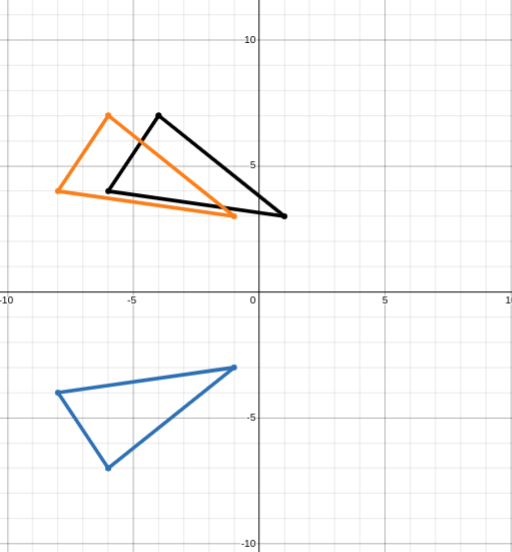
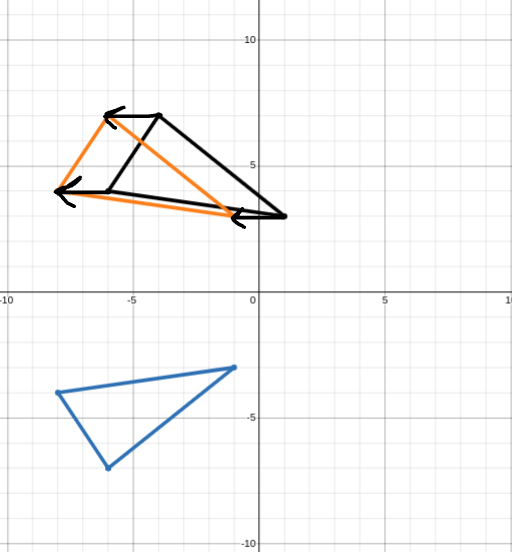
How can you translate the black △ to the orange △?

a. From black △ to the orange △, translate 2 units left.

b. From black △ to the orange △, translate 1 unit left.

c. From black △ to the orange △, translate 1 unit right.

d. From black △ to the orange △, translate 2 units right.

From black to orange, it can move 2 units to the left, so it’s -2.

a. From black △ to the orange △, translate 2 units left (-2).

This is the correct answer.