upcoming test (diffraction)

define path difference

the extra distance one set of waves travels with another

explain what occurs if the path difference between two waves is:

• an integer number of wavelengths

• (an integer +) a half number of wavelengths

1 — the waves end up in phase and constructive interference occurs where the waves meet

2 — the waves end up in antiphase and destructive interference occurs where the waves meet

if two waves start from 2 different points, what is the path difference?

there is one when the waves meet at any point

what is wave diffraction?

waves are diffracted through narrow gaps and around edges

all waves diffract

what is the requirement for waves to properly spread out when diffracting?

the gap must be of the order of one λ

how does the width of the gap affect wave diffraction?

a smaller gap leads to more diffraction, whereas a wider gap leads to less diffraction

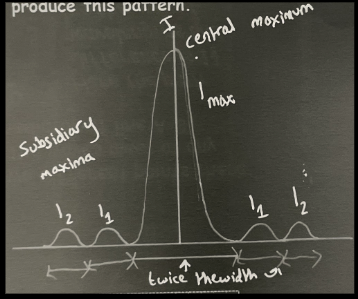
describe the single slit graph pattern (4)

in the single slit, each point in the slit acts as a source of the wave

in the centre, all waves meet in phase, producing a central maximum, with minima and maxima either side of it

the central maxima is about twice the width of the subsidiary maxima

as you get further from the centre, the maxima get smaller, with the central maxima being much higher than the rest

graph for the single slit diffraction pattern

what occurs to the graphs for diffraction patterns as the wavelength increases?

the pattern widens until only part of the central maxima can be seen

explain what is a coherent light source (3)

the light sources are of the same frequency

and have a constant phase difference

coherent light sources are used to make interference patterns. for the pattern to be seen easily…

the sources must be roughly the same amplitude

when preparing young’s double slits experiment, how can we achieve a coherent light source? give 2 ways

a laser, followed by a double slit

a single slit, followed by a double slit

when preparing young’s double slits experiment, how can we achieve a monochromatic light source? give 2 ways

a coloured filter can be put in front of the light source

a monochromatic light source can be used, instead of white light

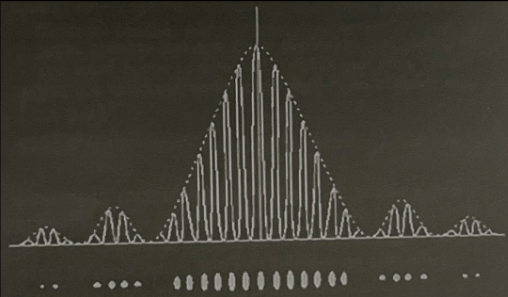
graph for young’s double slit pattern (realistic pattern)

graph for young’s double slit pattern (idealised pattern)

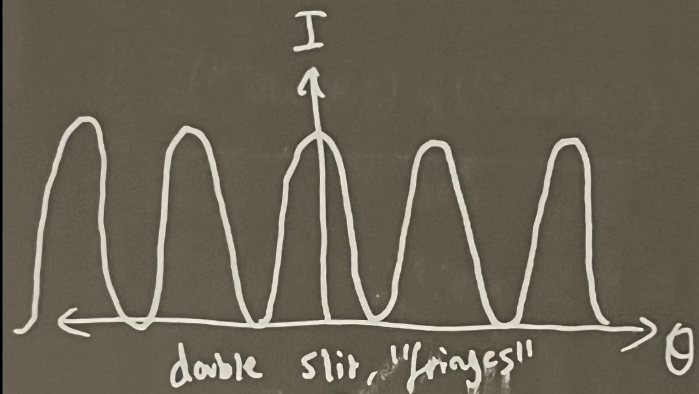
describe the young double slit graph pattern (4)

the maxima (called bright fringes) are separated by the same distance

the intensity falls off as you move from the central maximum

the minima are called dark fringes

the pattern is seen in the “area of overlap”

give typical distances for the following, in young’s double slits experiment:

• the slit widths

• the slit separation (s)

• the distance from the slits to the screen (D)

and which type of light source should be used

slit widths = 0.1mm

slit separation = 0.5mm

distance from slits to screen = 1m

monochromatic light

explain how we end up with the fringe spacing equation (2)

if monochromatic light is used (instead of white light) the fringes will be of one colour and have clearer edges

in this situation the diffraction pattern can be used to determine the wavelength of the light source

what is meant by each symbol in w=λD/s

w = fringe separation / distance between maxima 

λ = wavelength

D = distance from double slits to screen

s = slit separation 

in young’s double slits experiment, how is D measured?

metre rule

in young’s double slits experiment, how are s and w measured?

travelling microscope

give 2 sources of uncertainty in the young double slits experiment

the uncertainty in s is usually the greatest

the difficulty in measuring w is that only a few bright fringes may be seen, and they may be faint

give 2 ways of improving the accuracy of the young double slit experiment, and give an issue of one of them

we can make D larger, but then the fringes become fainter and more difficult to see

we can make s larger

what happens to the fringes if λ increases

the fringe spacing, w, will increase

what happens to the fringes if λ decreases

the fringe spacing, w, will decrease

what happens to the fringes if D increases

the fringe spacing, w, will increase

what happens to the fringes if D decreases

the fringe spacing, w, will decrease

what happens to the fringes if s increases

the fringe spacing, w, will decrease

what happens to the fringes if s decreases

the fringe spacing, w, will increase

what happens to the fringes if the slit width increases

more light is let through, so the fringes are brighter and blurrier

what happens to the fringes if the slit width decreases

the fringes are darker

in young’s double slit experiment, what causes the fringes?

diffraction occurs at the single slit, so both slits receive the waves

the two slits act as coherent light sources

diffraction at the two slits causes the waves to overlap

only in the area of overlap will fringes be seen

explain why do we see young’s double slits diffraction pattern (6)

refer to:

• how fringes are formed

• where bright and dark fringes are seen

• path difference

fringes are formed when light from the two slits overlap and superpose to produce the interference pattern

the slits emit coherent light

a bright fringe is formed where waves meet at the screen in phase and reinforce

a dark fringe is formed where waves meet at the screen in antiphase and cancel

the path difference from the slits to the fringe is equal to a whole number of wavelengths for a bright fringe

and a whole number + ½ a wavelength for a dark fringe

how do we get a diffraction pattern of bright and dark fringes? (2)

bright fringes occur where there is constructive interference

dark fringes occur where there is destructive interference

what is meant by each symbol in d sinθ=nλ

d = slit separation

θ = angle of diffraction for a specific maximum

n (or m) = order of the maximum

λ = wavelength

graph for diffraction grating

explain how to derive d sinθ=nλ (1):

• drawing the diagram

draw:

• the double slits

• parallel light rays going into the centre of each slit

• label the centre of each slit as A and C

• a light ray emerging from each slit going at a slight angle, still parallel to each other

• arrowheads on the light rays

explain how to derive d sinθ=nλ (2):

• getting the required values

draw:

• the perpendicular of the light ray, going to A

• at the perpendicular, label B

• the light ray going into C continued

• the angle under B as θ

• a perpendicular at C, parallel to the perpendicular at B

explain how to derive d sinθ=nλ (3):

• deducing the equation

understand that:

• a triangle ABC is formed where the hypotenuse is equal to d (slit separation) and the angle theta under B is the same as the angle under A

• using trigonometry BC = d sinθ

• BC is equivalent to the path difference, which, for constructive interference (and hence a maximum) is an integer value of wavelengths

• n is referred to as the order of the maximum

explain why do we see the diffraction grating pattern (6)

refer to:

• how maxima are formed

• where maxima and minima are seen

• path difference

maxima are formed when light from the slits overlap and superpose to produce the interference pattern

the slits act as coherent light sources

a maximum is formed where waves meet at the screen in phase and reinforce

a minimum is formed where waves meet at the screen in antiphase and cancel

the path difference from the slits to the fringe is equal to a whole number of wavelengths for a maximum 

and a whole number + ½ a wavelength for a minimum