Thermodynamics S1

note: this does not include a lot of the derivations and long form example explanations. this is mainly for terms/definitions and basic equation explanations

zeroth law (description)

defines TEMPERATURE (T):

for two bodies to be in thermal equilibrium with each other, they must have the same temperature, and vice versa. This property exists for every thermodynamic system.

first law (description)

defines INTERNAL ENERGY (U):

This property exists for every thermodynamic system. Change in internal energy = mechanical work done on the system (adiabatic process) or = heat added to system - mechanical work done by the system (non-adiabatic)

second law (description)

defines ENTROPY (S):

An extensive scalar property that exists for every thermodynamic system in equilibrium such that dS = dQ/T where T is the absolute temperature and dQ is the amount of heat received by system. It can never decrease. It is constant if and only if all processes are reversible.

what is thermodynamics?

theory of relations between heat and mechanical energy, and the conversion of either into the other.

engine

a machine designed to convert one or more forms of energy into mechanical energy

heat engine

a physical or theoretical device that converts thermal energy into mechanical output.

carnot heat engine

hypothetical engine that runs on the reversible carnot heat cycle

directly observable quantities

can be directly measured e.g. temperature, pressure, volume

thermodynamic system

defined by three components: the system, the surroundings and the boundary between them.

homogeneous

properties of a system are uniform throughout and system consists of a single phase.

heterogenous

when a system contains more than one phase or its properties vary within it.

Surrounds and boundary

Surroundings - everything apart from the system. The system can interact with the surroundings by exchanging matter or energy across the boundary.

isolated system

neither matter not energy can be exchanged

closed system

only energy can be exchanged, not matter (so number of particles is constant)

open system

energy and matter can be exchanged

heat bath/reservoir

a system so large that its temperature (T) is not affected by heat flow. dT → 0 if heat capacity C → 0 because dT = dQ/C

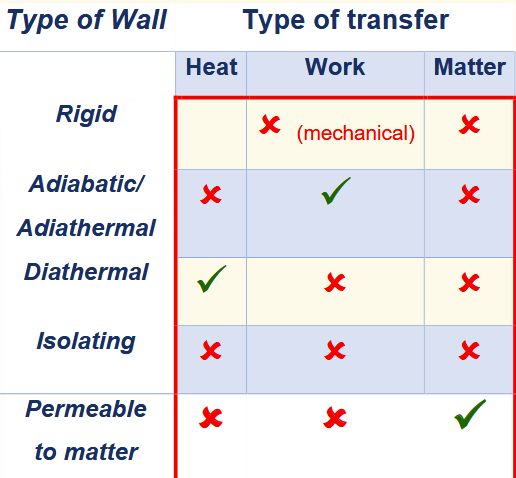
rigid wall

prevents system from changing its volume/shape so no mechanical work can be done on the system

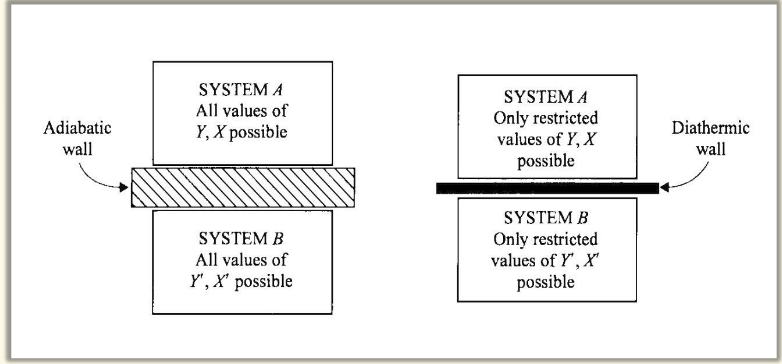
adiabatic wall

prevents any thermal interaction. can also be described as thermally isolated.

adiabtic changes

when a system cannot exchange heat, but work is still done on it, those changes are adiabatic.

diathermal walls

allow a system to be influenced thermally (non-adiabatic). Two systems with a diathermal wall between them are said to be in thermal contact.

type of wall / type of transfer table

thermodynamic equilibrium

when a system is simultaneously in:

• mechanical equilibrium (constant pressure)

• chemical equilibrium (constant particle concentration)

• thermal equilibrium (constant temperature)

when at equilibrium, a thermodynamic system is defined by:

the state variables only, not the history of the system (the previous conditions it existed in)

equation of state

equation that links different state variables (the macroscopic properties that define a system, like volume and temperature). e.g. Ideal Gas Law pV = nRT

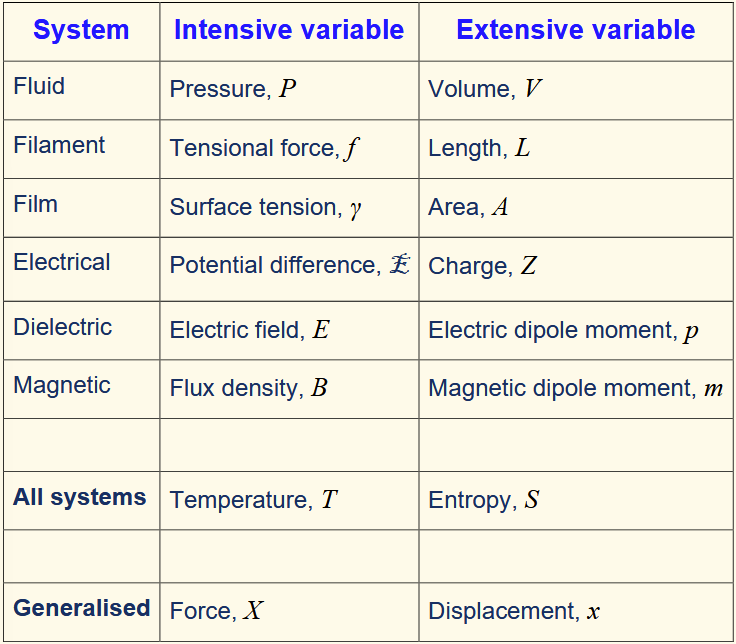
extensive variable

state variable dependent on the system’s size e.g. volume, mass, internal energy entropy

intensive variable

state variable independent of the system’s physical size e.g. temperature, pressure, density

conjugate pairs

Extensive and intensive pair of state variables for a system whose product have the dimension of energy

thermodynamic process

when a system goes through a series of changes that takes it from an initial state to a different final state

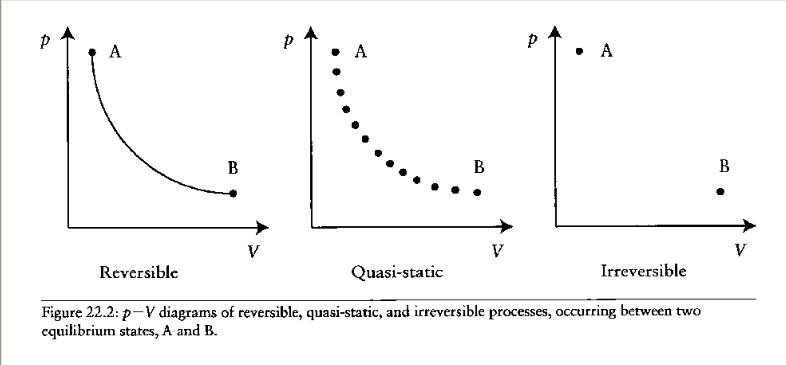
reversible process

if and only if its direction can be reversed by an infinitesimal change in conditions (not enough if it can only be reversed by a finite change)

conditions for thermodynamic reversibility

quasistatic process and no hysteresis

quasistatic process

process carried out so slowly (infinitely slowly) that every state the system passes through can be considered an equilibrium state

hysteresis

when a process in a system is reversed, it does not retrace its previous path and follows a different one e.g. stretching of a rubber band

irreversible process

when energy is permanently lost from the system due to dissipative forces like friction. Hysteresis in a process implies energy has been dissipated from the system.

reversible, quasistatic and irreversible process diagrams

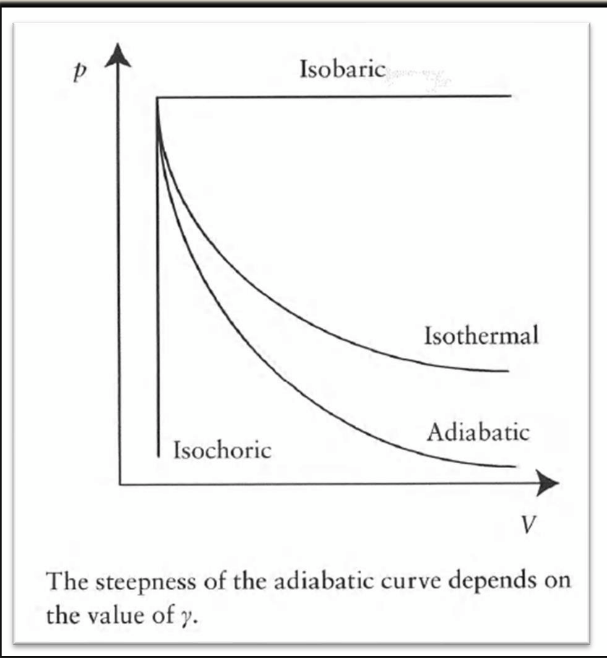
4 common reversible processes

• isothermal: temperature remains constant, PV = constant

• isochoric: volume remains constant, P/T = constant

• isobaric: pressure remains constant, V/T = constant

• adiabatic: no heat exchanged between system/surroundings: PV^γ = constant

what is γ

the ratio of the constant pressure to constant volume heat capacities

f is degrees of freedom of motion of the gas

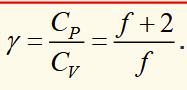
another ideal gas equation

U: internal energy

f: number of activated degrees of freedom

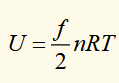
thermal equilibrium

state achieved by 2(+) systems after they have been in thermal contact with one another, characterised by the restricted values of their coordinate systems. There is no net heat flow between systems.

heat

thermal energy in transit

thermalisation

the process leading to thermal equilibrium

zeroth law

if two systems are separately in thermal equilibrium with a third system, they must also be in thermal equilibrium with each other

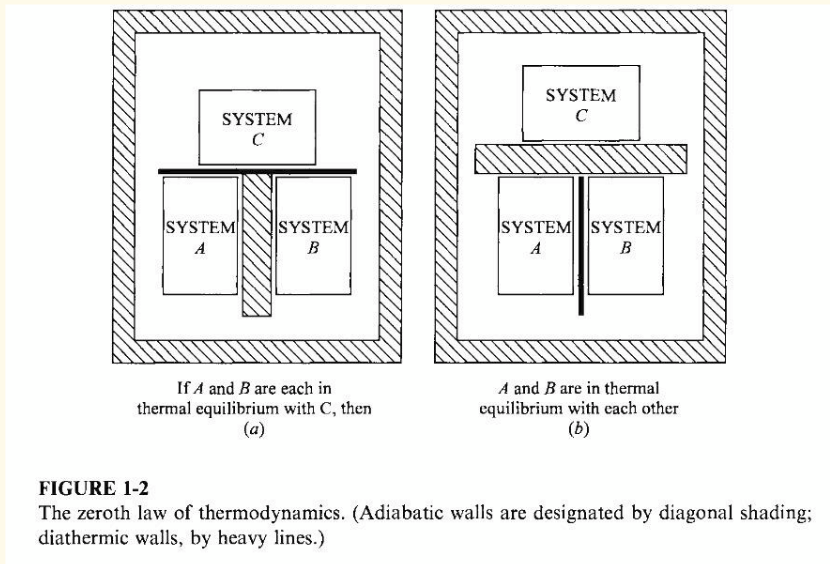
equation of state for 3 systems in thermal equilibrium

Φ(P,V) = Θ

Θ = empirical temperature, and is the same for all systems

when 2(+) systems are in thermal equilibrium, (for each one) a function of the parameters only takes a common value.

1 Kelvin

the fraction 1/273.16 of the thermodynamic temperature of the triple point in water

sign of work done on system

positive when done ON system

negative when work done BY system on surroundings

differential of work done on a system

P_ext = external pressure

dw = inexact differential (value of integral depends on the path)

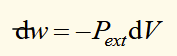
work done on a system when there is a finite change in volume

line integral i.e. dependent on path

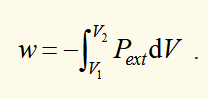
work done on a system when there is a finite change in volume (quasistatic case)

P_ext = P = P(T,V) (it can be treated as equilibrium, so external pressure = pressure of gas (function of temperature and volume))

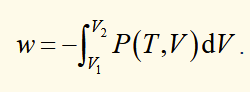
internal energy (U)

The property of the system whose change is found through expressing the change of state (independent of path) in an adiabatic process in terms of the work required.

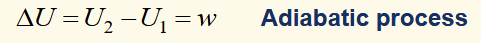
describe heat and work

forms of energy crossing a boundary

sign of heat (Q)

+Q indicates heat is absorbed by system from surroundings

-Q indicates heat is lost by system to surroundings

internal energy of a closed system in which no work is done

It is equal to the heat absorbed

first law

Energy is conserved and heat and work are both forms of energy.

ΔQ: heat supplied TO system

Δw: work done ON system

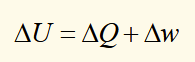
differential change in internal energy

dQ and dw are inexact differentials

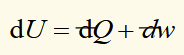
common contributions to work done on a system in infinitesimal reversible changes

heat capacity of a system

α is the variable kept constant in the partial differentiation of Q with respect to T. from 0th law we know that Q is a function of T only, so we can use a total derivative.

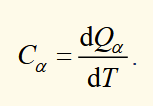
heat capacity at constant volume ****

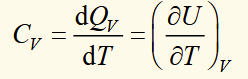
internal energy for a reversible process

shows that internal energy of an ideal gas depends only on temperature

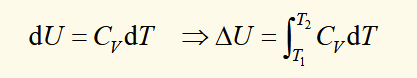
heat capacity at constant pressure

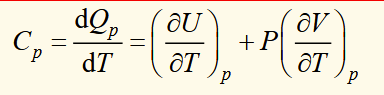
derivation of C_v and C_p for general ideal gas

adiabatic condition on pressure and volume

In a thermally isolated system: for an adiabatic process, there is no heat exchange between a system and its surroundings (dQ = 0)

work done on gas for an adiabatic change

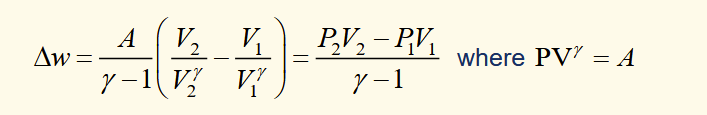
change in heat for isochoric process

heat change for isobaric expansion

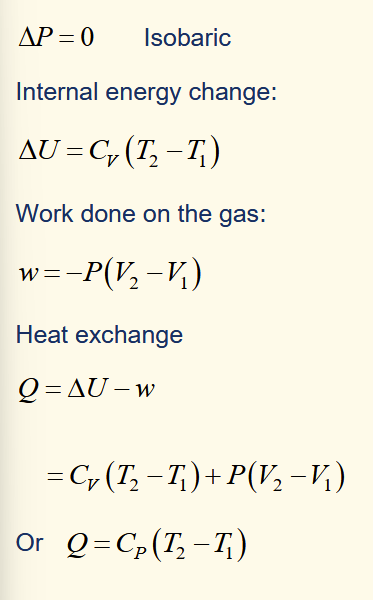
adiabat vs isotherm

isotherm so C is constant: dP/dV = -P/V

adiabat: dP/dV = -γP/V

so, on a P-V graph, an adiabat will always be steeper than an isotherm

second law (overview)

no process is possible were the total entropy of the universe decreases. Change in entropy is always greater than or equal to 0.

definition of a small change in entropy

small changer in heat flow per unit temperature into the system, providing heat flow corresponds to a reversible process

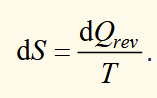
carnot heat engine (expanded)

heat engine that uses heat to generate mechanical work by carrying a ‘working substance‘ through a cyclic process

steps of carnot cycle

step 1: ΔU1 = Q1 + w1

step 2: ΔU2 = w2

step 3: ΔU3 = Q2 + w3

step 4: ΔU4 = w4

ΔU_cyc = (Q1 + Q2) + (w1 + w2 + w3 + w4) = 0

|w_cyc| = |Q1|- |Q2|

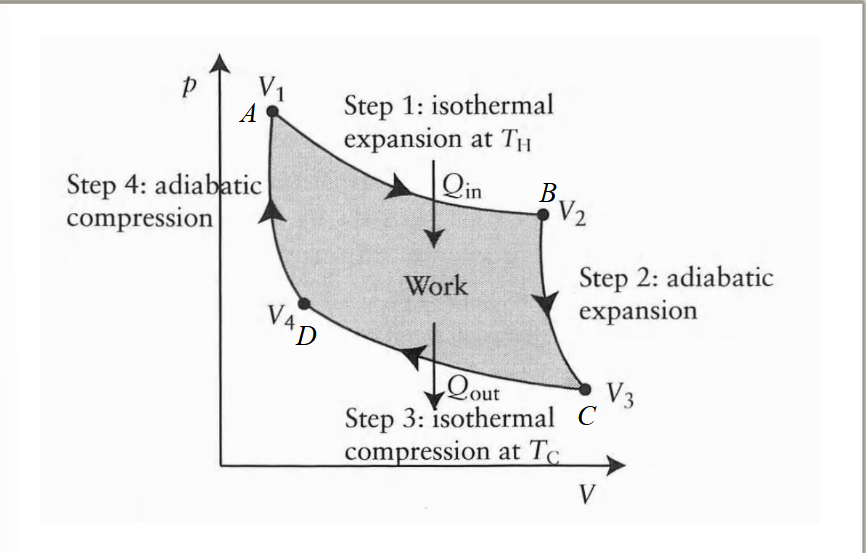
efficiency of a heat engine

ratio of work done on surroundings to the heat input at higher temps. this can also be expressed in terms of |Q1| and |Q2|

Kelvin statement

no process is possible whose sole result is the complete conversion of heat into work

Clausius statement

no process is possible whose sole result is the transfer of heat from a colder to a hotter body

carnot cycle for an ideal gas: important results

thermodynamic (definition of) temperature

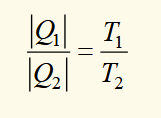
efficieny of an engine using thermodynamic temperature

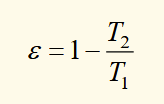
heat/temperature relation for the reversible cycle of a carnot engine

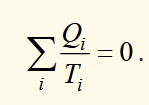
change in entropy around a reversible cycle

the integral symbol shows its integrating about a cycle

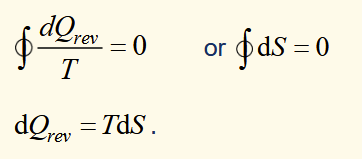
carnot’s theorem

no engine operating between two given reservoirs can be more efficient than a carnot engine operating between the same two reservoirs.

statement about efficiency of reversible engines

all reversible engines working between two temperatures have the same efficiency ε_c

isentropic process

process which is both adiabatic and reversible (so entropy doesn’t change)

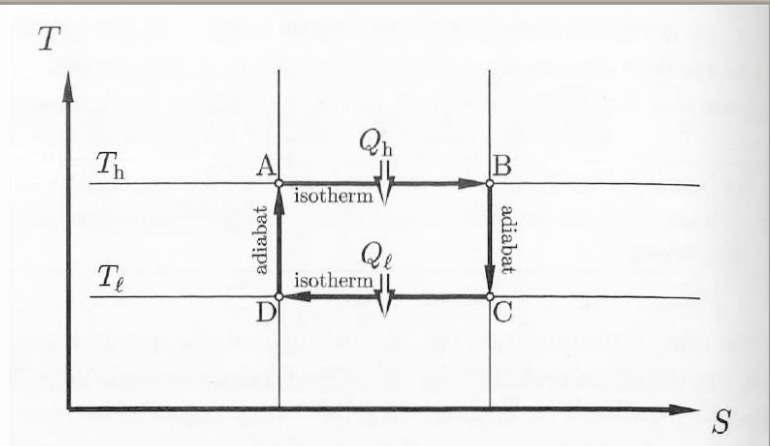
efficiency of a fridge

reverse heat pump. work is put in to make heat flow from cold reservoir to hot reservoir

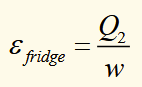
efficiency of carnot engine fridge

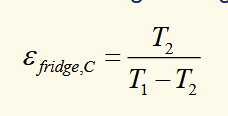
heat pump

work is put into system to pump heat from reservoir to somewhere it is wanted. we want to supply as much heat as possible for little external work, so efficiency can be >1

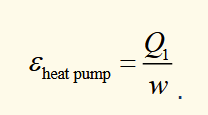
efficiency of carnot engine heat pump

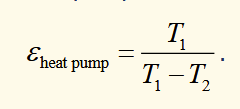
Clausius Theorem (Inequality)

based on comparing efficiencies of a general engine to a reversible one, linking to thermodynamic temperature then comparing heat/temperature ratios, where ΣQi/Ti = 0 for reversible and ≤ 0 for general non reversible engine.

Clausius Theorem (elaboration)

• if any part of the cyclic process is irreversible (natural) the the inequality applies

• if a cyclic process is reversible, then equality applies as we have seen for reversible carnot

• it is impossible for the cyclic integral to be greater than 0.

second law (useful form)

for an infinitesimal irreversible process in an isolated process, the change in entropy is greater than the differential of heat divided by temperature at which heat is supplied.

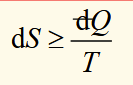
three types of processes (in terms of dS)

• sponatneous and irreversible process: dS > dQ/T

• reversible process: dS = dQ/T

• impossible process: dS < dQ/T

impossible process

it is impossible for a process in an isolated system to reduce entropy.

change in entropy over time

when a natural process occurs in an isolated system, there is an increase in entropy. Entropy reaches a maximum at equilibrium. Thus, the increase in entropy indicates the time sequence of natural events (arrow of time)

change in entropy

[1 and 2 refer to states 1 and 2 of the system]

this shows that there cannot be a change in entropy without a change in state. Heat and entropy can flow through an unchanged part of a system.

finding change in entropy (steps)

1) apply first law of thermodynamics and any equation of state to the irreversible process to find the final thermodynamic equilibrium state of the system

2) ignore details and only consider initial and final thermodynamic equilibrium states

3) devise a (simple) reversible path between these states (does not need to resemble original process at all, as long as beginning and end are the same)

4) evaluate the integral dQ/T from the initial state to the final state. This is the change in entropy ΔS

second law (one final time)

The entropy of an isolated system tends to a maximum.

Apply this to Universe (modelled as a closed system) and you realise we are heading to the heat death of the universe.