The Derivative + velocity
Call Kai
Learn
Practice Test
Spaced Repetition
Match
Flashcards
Knowt Play1/11
There's no tags or description
Looks like no tags are added yet.
Name | Mastery | Learn | Test | Matching | Spaced | Call with Kai |
|---|
No analytics yet
Send a link to your students to track their progress
12 Terms
What is the definition of a derivative? (given its condition?)
What is an alternative definition?
What is the formula for finding the derivative of f at any a?
Definition:
IF:
lim [f(x)-f(a)]/x-a exists,
x→a
THEN:
f ’(a) = lim [f(x)-f(a)]/x-a
x→a
f’(a) = derivative of a function f at a number a (“f prime of a”)
If the limit does NOT exist, then we say - “the function is not differentiable at the number a”
Alternative definition:
f’(a) = lim [f(a+h)-f(a)]/h
h→0
(let h=x-a)
Formula for finding the derivative of f at any a:
f’(x) = lim [f(x+h)-f(x)]/h
h→0
Conceptually, what is a derivative?
The slope at any point of your curve
What does it mean when f is differentiable at a?
f’(a) exists
(derivative of function f exists at a)
When is f differentiable on an open interval? Which ones?
f is differentiable on an open interval IF it is differentiable at every number in the interval
(a,b)
(a,∞)
(-∞,a)
(-∞,∞)
If f(x)=x²-2x, find a formula for f’(x)
answer
What is the Leibnitz notation for f’(x) and f’(a)?
Leibnitz notation for f’(x) and f’(a):
d/dx (f(x)) = f’(x)
df/dx = f’(x)
df/dx | x=a = f’(a)
How would you know if f is continuous at a from the function’s differentiability?
image
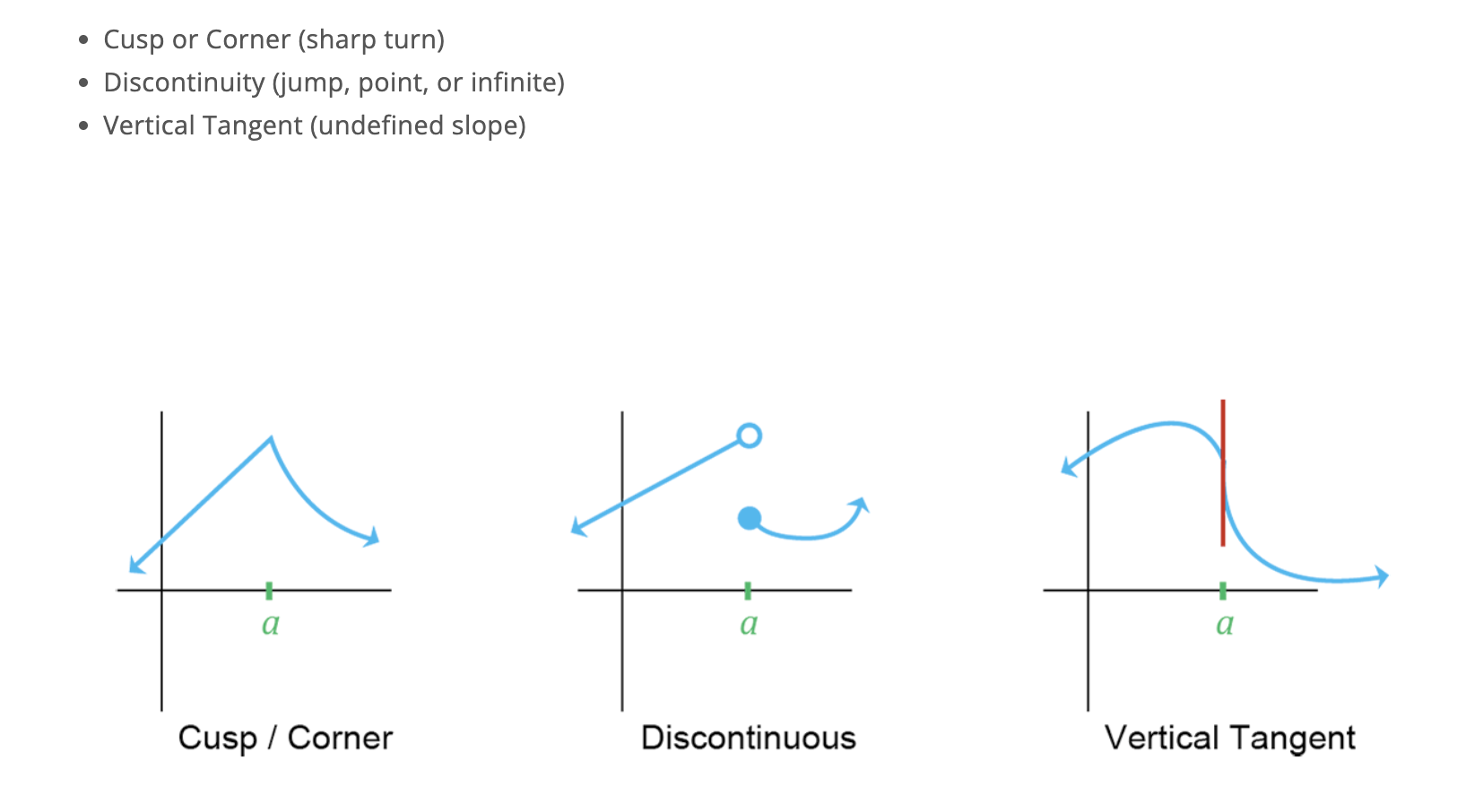
How can functions FAIL to be differentiable?
If lim x→a [f(x)-f(a)]/x-a is infinite (can also be on one side only too)
graph is not smooth (sharp lines)
Vertical tangent line
How would you prove that f(x) = cube root of x is not differentiable at x=0?
answer
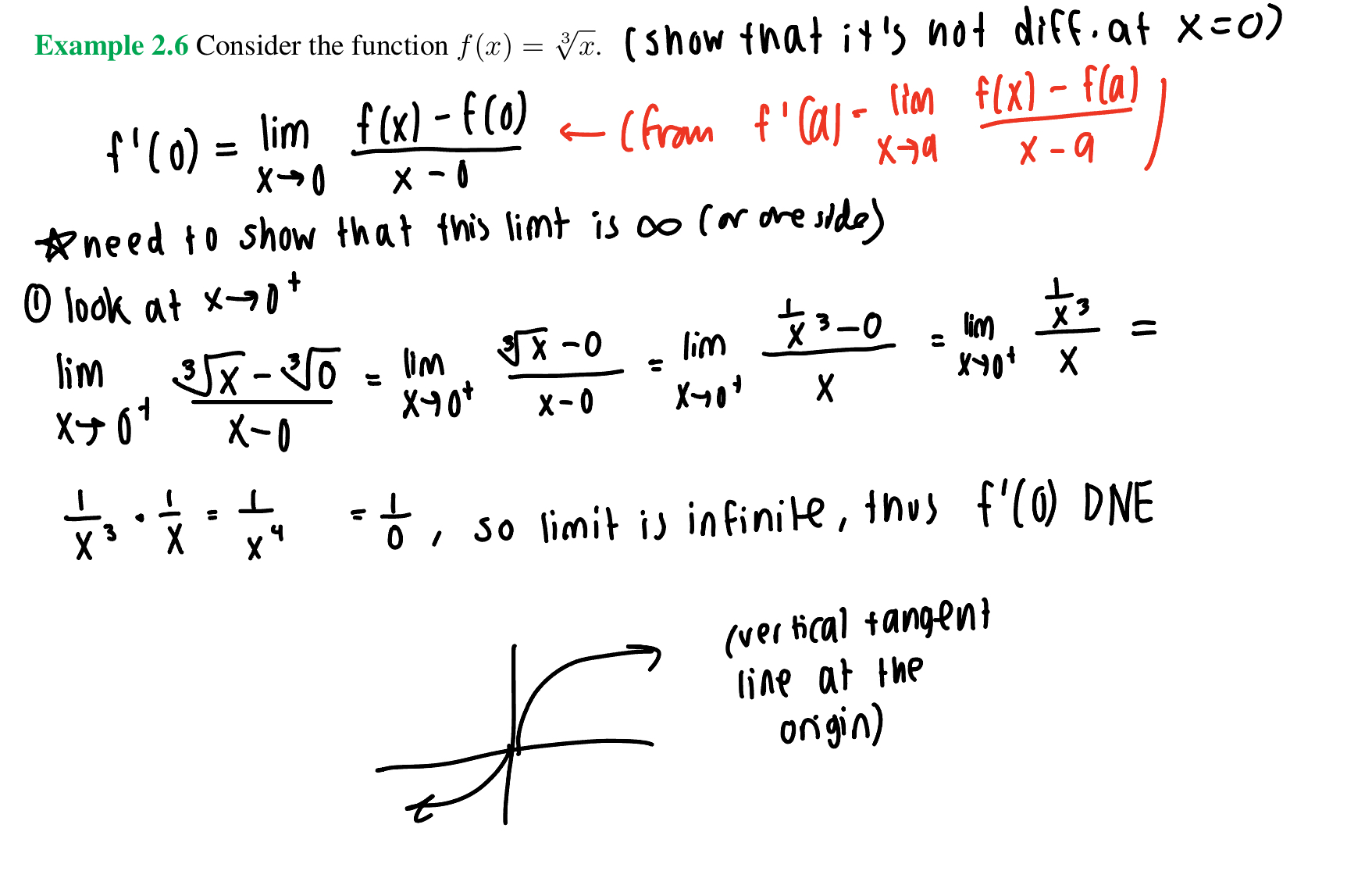
True or false: If a function f(x) is continuous at x=a, then f(x) is differentiable at x=a
FALSE
ex) Just because a function is continuous and a limit exists doesn’t mean its differentiable
ex) f(x)=|x| has sharp lines (no smooth curves), so f(x) is not differentiable even though it is continuous at a point a
Graphically, how can you visually see where a point is not differentiable?
Image
How do you interpret these derivatives?
f’(2)=0
f’(2)>0
f’(2)<0
f’(2)=0 → slope of tangent is 0
f’(2)>0 → slope of tangent is >0 (f is INCREASING near 2)
f’(2)<0 → slope of tangent is <0 (f is DECREASING near 2)
