ECON 320: Econometrics Final

Q: What is the minimum requirement for an estimator to be considered acceptable?

The minimum requirement is consistency: as sample size increases, the estimator’s sampling distribution collapses around the true parameter so the estimator converges in probability to that true value.

What does it mean for an estimator Betajhat to be consistent for Betaj?

Betajhat is consistent if, as the sample size n→∞n \to \inftyn→∞, the probability that Betajhat is arbitrarily close to Betaj goes to 1; equivalently, the distribution of Betajhat becomes more and more tightly concentrated around Betaj.

State Theorem 5.1 (Consistency of OLS) from the notes

Under assumptions MLR 1–4, the OLS estimator Betajhat is a consistent estimator of Betaj for all j=0,1,…,kj = 0,1,\dots,kj=0,1,…,k; that is, plim(Betajhat) = Betaj

In the simple regression case, what is the key probability-limit argument used to show that Beta1hat is consistent?

Under MLR 4 (zero mean and zero correlation between xi​ and ui), the numerator has probability limit 0 and the denominator has probability limit Var(xi) > 0, so plim(Beta1hat) = Beta1

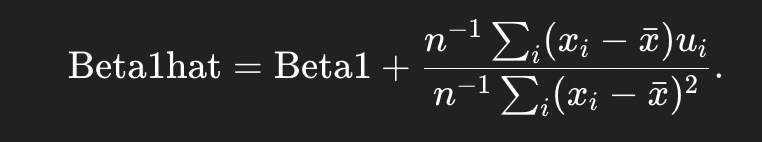
Define the “probability limit” (plim) as used in the consistency proof.

The probability limit of an estimator is the value it converges to in probability as the sample size grows without bound; it is “the value to which an estimator converges as the sample size grows without bound.”

State Assumption MLR 4′ from the notes and explain how it differs from the usual MLR 4.

MLR 4′ (four-prime) requires zero mean and zero correlation: E(u) = 0 and Cov(xj, u) = 0 for all j = 1,…,k. This is weaker than the usual MLR 4, which requires the zero conditional mean E(u | x1,…,xn) = 0, meaning the error has mean zero given the entire set of regressors.

According to the notes, what happens to OLS estimators if the error term is correlated with any of the independent variables?

If the error term is correlated with any independent variable, OLS estimators are biased and inconsistent; correlation between u and any xj generally causes all OLS estimators Betajhat to be inconsistent.

Q: Give the formula for the inconsistency of Beta1hat when Cov(x1, u) ≠ 0.

In the omitted variable setup, let the true model be y = Beta0 + Beta1 x1 + Beta2 x2 + v satisfying MLR 4. If we instead estimate y = Beta0tilde + Beta1tilde x1 + u omitting x2, what is plim(Beta1tilde)

Under what condition does the omitted-variable estimator Beta1tilde become consistent for Beta1?

If x1 and x2 are uncorrelated, then Cov(x1, x2) = 0 so δ1 = 0, and thus plim(Beta1tilde) = Beta1; in that case, omitting x2 does not create inconsistency.

Do we reduce inconsistency by simply adding more regressors to the model if one regressor is correlated with the error term? Explain.

No. The notes say inconsistency does not improve if you add more regressors; if x1 is correlated with u but the other independent variables are uncorrelated with u, then all OLS estimators Betajhat are generally inconsistent.

Why have the notes emphasized the “normal” (stronger) MLR 4 assumption up to now instead of only MLR 4′?

Because under just MLR 1–3 and MLR 4′, OLS can still be biased if E(u | x1,…,xn) ≠ 0; under the stronger MLR 4, we can write the conditional mean of y as a linear function
E(y | x) = Beta0 + Beta1 x1 + … + Betak xk,
which allows us to interpret the Betaj as partial effects. With only MLR 4′, this linear form need not equal the true population regression function, and non-linear functions of the xj (like xj²) could still be correlated with the error.

Under what assumptions do we have the asymptotic normality of OLS?

MLR 1-5

What 3 things does the asymptotic normality of OLS tell us?

1. Bj are asymptotically normally distributed.

2. Sigmahat² is a aconsistent estimator of Sigma² = Var(u)

3. Under MLR 1-5, t-stat is asymptotically standard normal. Under MLR 1-6, t-stat has an exact t-distribution regardless of sample size

Which assumption out of CLM do we not need for the asymptotic normality of OLS?

MLR 6: Normally distributed errors and independence from explanatory variables

What do we need for asymptotic test statistics and standard errors to hold?

Large samples

Describe the steps for the Lagrange Multiplier test when asymptotic

1. Regress y on the restricted set of ind. variables and obtain u from this regression

2. Regress u on all the independent variables (restricted and unrestricted) and obtain the R²u from this

3. Compute LM = nR²u

4. Compare LM to the appropriate critical value c in the chi² distribution. If LM > c, reject the null

Describe what the LM Statistic Test does

The LM statistic allows us to jointly test whether relaxing a set of restrictions on the model, (setting some coefficients to zero), significantly improves the fit. It has an approximate chi-square distribution under asymptotic normality and the null. Large values lead us to reject the null.

What does it mean for an estimator to be asymptotically efficient?

An estimator is asymptotically efficient if, among a specified class of consistent estimators, it has the smallest possible variance in large samples

What 2 characteristics of OLS does MLR 1-5 deliver?

1. BLUE

2. Asymptotic Efficiency

Prove the consistency of OLS estimators under MLR 1-5.

Define convergence in Probability

Convergence is when a sequence of RVs Xn converge to some random variable X. This occurs if, for any small value epsilon > 0, the probability that |X - Xn| > epsilon goes to zero as n approaches infinity.

Define convergence in distribution.

A sequence of RVs Xn converges in distribution to an RV X if the distribution functions converge at all continuous points of the limit CDF

How are unbiasedness and consistency related to one another?

Unbiasedness is a finite sample property, whereas consistency is asymptotic. An estimator can be both unbiased and inconsistent if its variance doesn’t shrink with n, just as it can be both biased and consistent if the biasedness goes to zero as n grows.

What are 2 major consequences of Omitted Variable Bias?

OLS estimators are generally biased and inconsistent

What kind of problem is using IVs meant to address?

An endogeneity problem of >= 1 independent variables

In the simple regression model y=Beta0+Beta1x+uy = Beta0 + Beta1 x + uy=Beta0+Beta1x+u, what is the situation in which IV is needed instead of OLS?

We need IV when we think x and u are correlated (Cov(x, u) ≠ 0); if x and u are uncorrelated, we should just use OLS.

State the two conditions that a variable z must satisfy to be a valid instrumental variable (IV) for x in the simple regression.

(1) z is uncorrelated with u: Cov(z, u) = 0 (exogeneity); (2) z is correlated with x: Cov(z, x) ≠ 0 (instrument relevance)

How do we test the instrument relevance condition in practice for a single IV z and regressor x?

Estimate x = pi0 + pi1z + v. pi1 = Cov(pi,x)/Var(pi1) holds if pi1 does not equal zero, so then we can reject the null of pi1 = 0.

What is a formula for the IV estimator of B1?

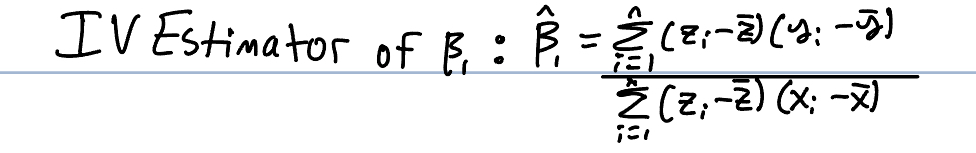
What distribution does the IV estimator have?

Approximately normal in large sample sizes

What is the estimated variance of the IV estimator and how does it compare to that of the OLS estimator?

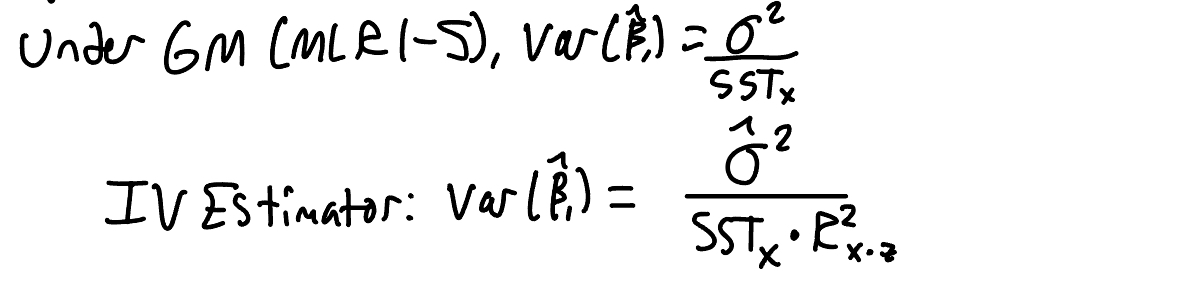
Which assumption fails for us to use IV? Which ones do we still need?

MLR 4 fails due to the endogeneity problem, but we still use MLR 1-3 and potentially homoskedasticity.

When is IV a consistent estimator?

When z and u are uncorrelated and z and x have any covariance other than 0

Give the formulas for the probability limits of both the IV estimator and of the OLS estimator.

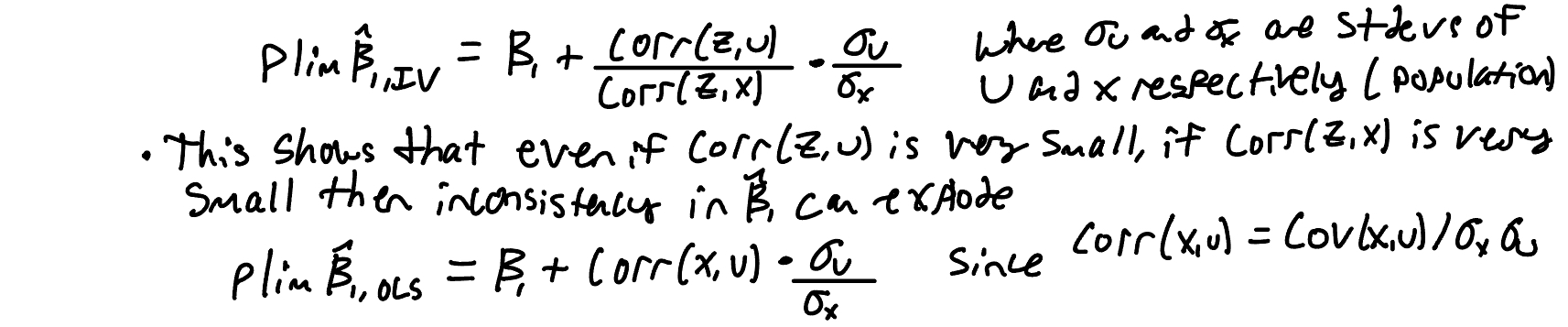
What are the steps of the Breusch-Pagan Test?

1. Estimate the model via OLS, then obtain uhat²

2. Regress uhat² on all of the explanatory variables (new coefficients of course) and keep the R² from this

3. Form either the F stat or LM stat for significance of the whole regression

Describe the White Test for heteroskedasticity

It is the LM statistic for testing that all of the coefficients in the regression of uhat² on each of the independent variables, their squares, and their cross products are zero.

Describe the alternative way of computing a White test

1. Estimate the mode by OLS as usual. Obtain the uhat and yhat. Compute uhat² and yhat²

2. Regress uhat² on both yhat and yhat², alongwith an intercept. Obtain the R² from this

3. Form either the F or LM statistics and compute the p-value

Q: Why does omitting an important variable generally make the OLS estimator biased, and when does it also become inconsistent?