Orbital Mechanics 1

Additional Reading: Orbital Mechanics for Engineering Students Curtis Butterworth Heinemann, 2013

Orbital Geometry

Ellipse

Conic Section

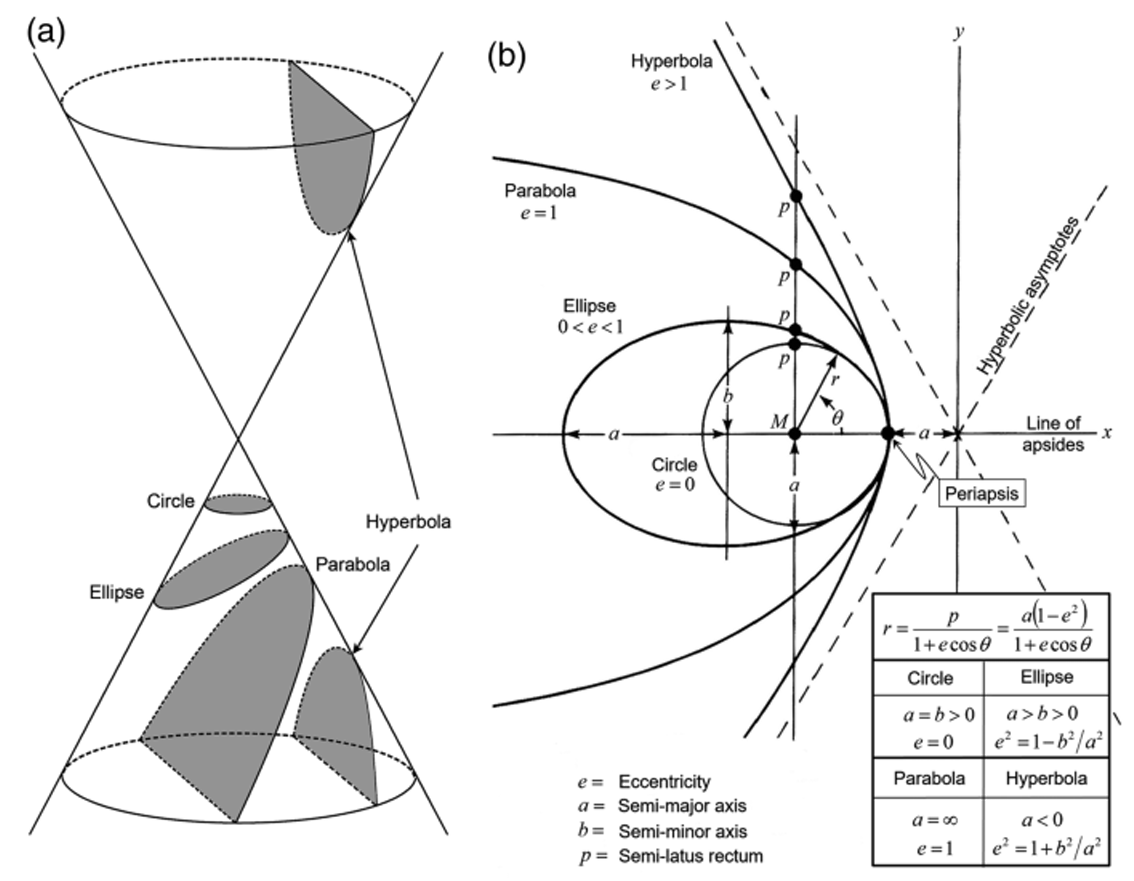
Definition: It’s a curve formed by the intersection between a plane and a right circular cone. Orientation of plane determines type of conic section

Circle: Plane perpendicular to axis of cone to create bounded curve

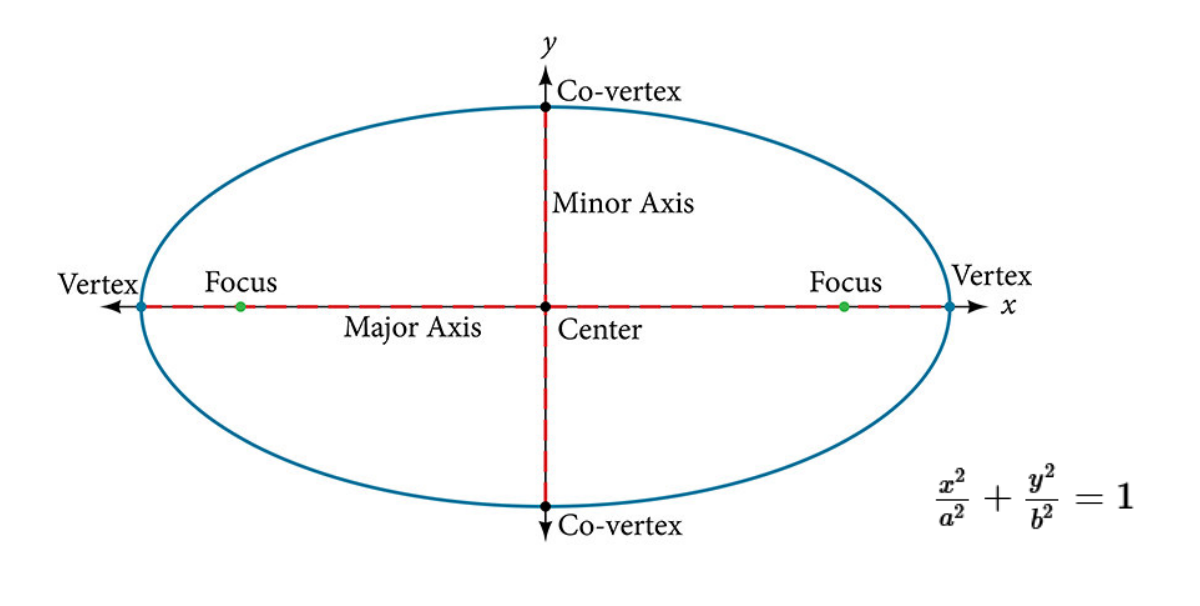
Ellipse: Intersection between plane and cone in general to create bounded curve

Parabola: Plane parallel to generator line of cone to create unbounded curve

Hyperbola: Intersection between plane and cone to create unbounded curve and plane NOT parallel to generator line

Dependend on…

• Eccentricity

• semi-major axis

• energy

Newton’s Law of Universal Gravitation

How does Newtons Second Law of Motion and Newton’s Law of Universal Gravitation relate to each other

where:

g_0: standard gravity; nominal gravitational acceleration of an object in a vacuum near the surface of the Earth

μ: standard gravitational parameter; for two bodies, the parameter may be expressed as G(m1 + m2), or as GM when one body is much larger than the other

Newton’s Gravitational Law

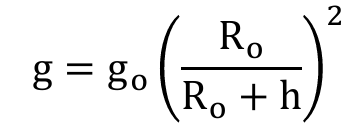
What is the First Law of Kepler’s Laws of Planetary Motion ?

1. The Law of Ellipses: “The orbit of every planet is an ellipse with the sun at one of the foci.”

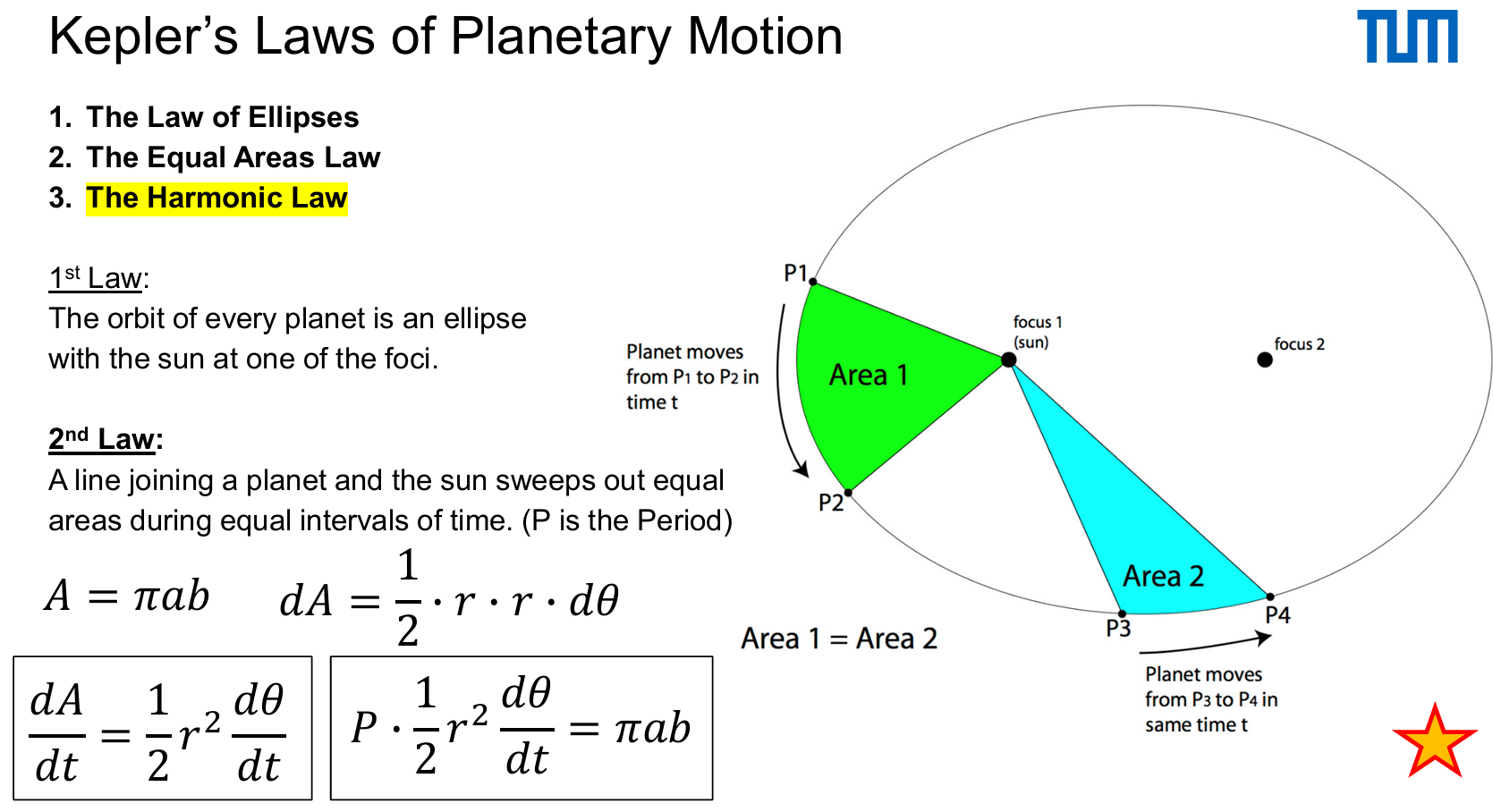
What is the Second Law of Kepler’s Laws of Planetary Motion ?

2. The Equal Areas Law: “A line joining a planet and the sun sweeps out equal areas during equal intervals of time. (P is the Period)”

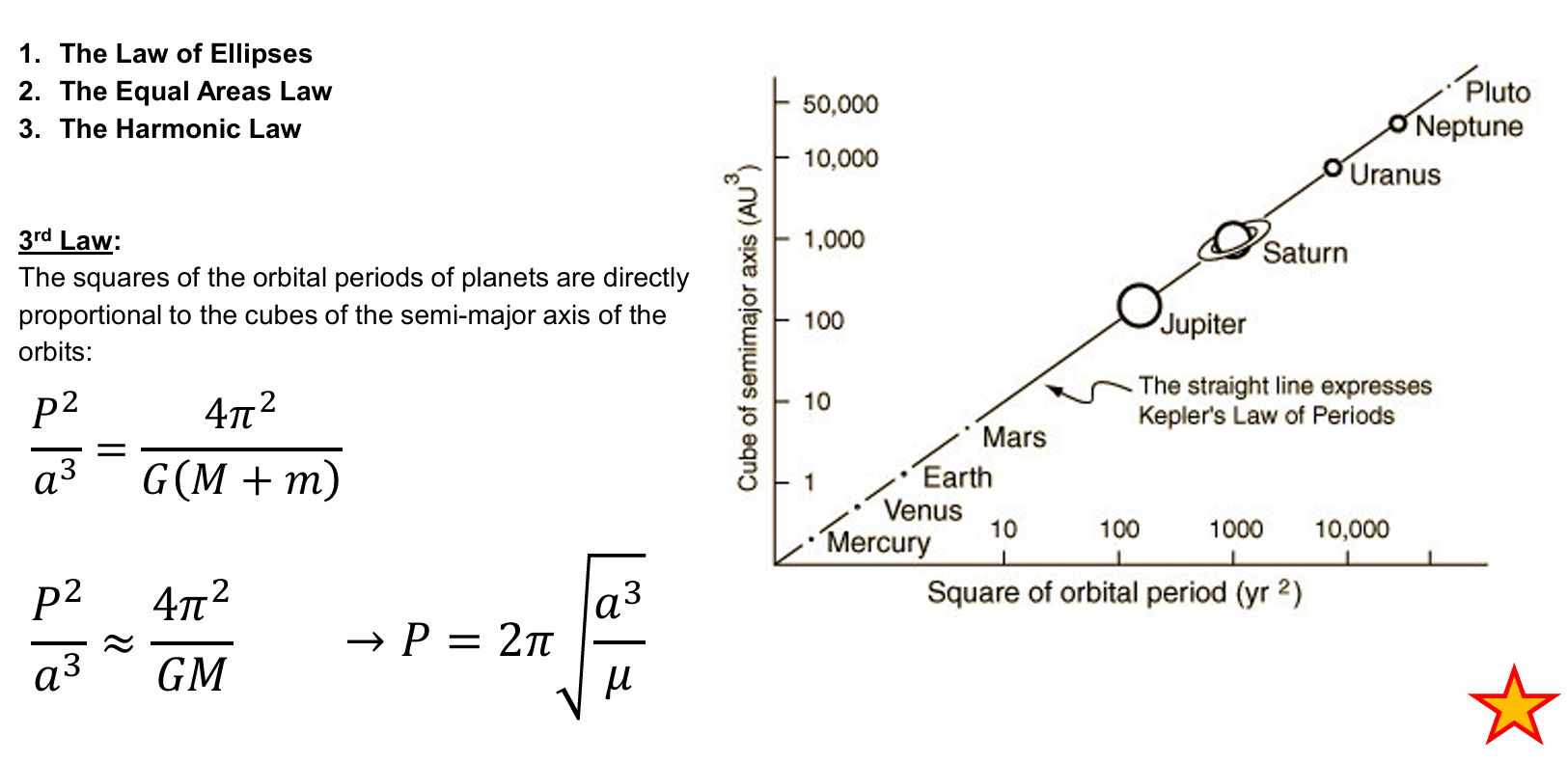
What is the Third Law of Kepler’s Laws of Planetary Motion ?

3. The Harmonic Law: “The squares of the orbital periods of planets are directly proportional to the cubes of the semi-major axis of the orbits:

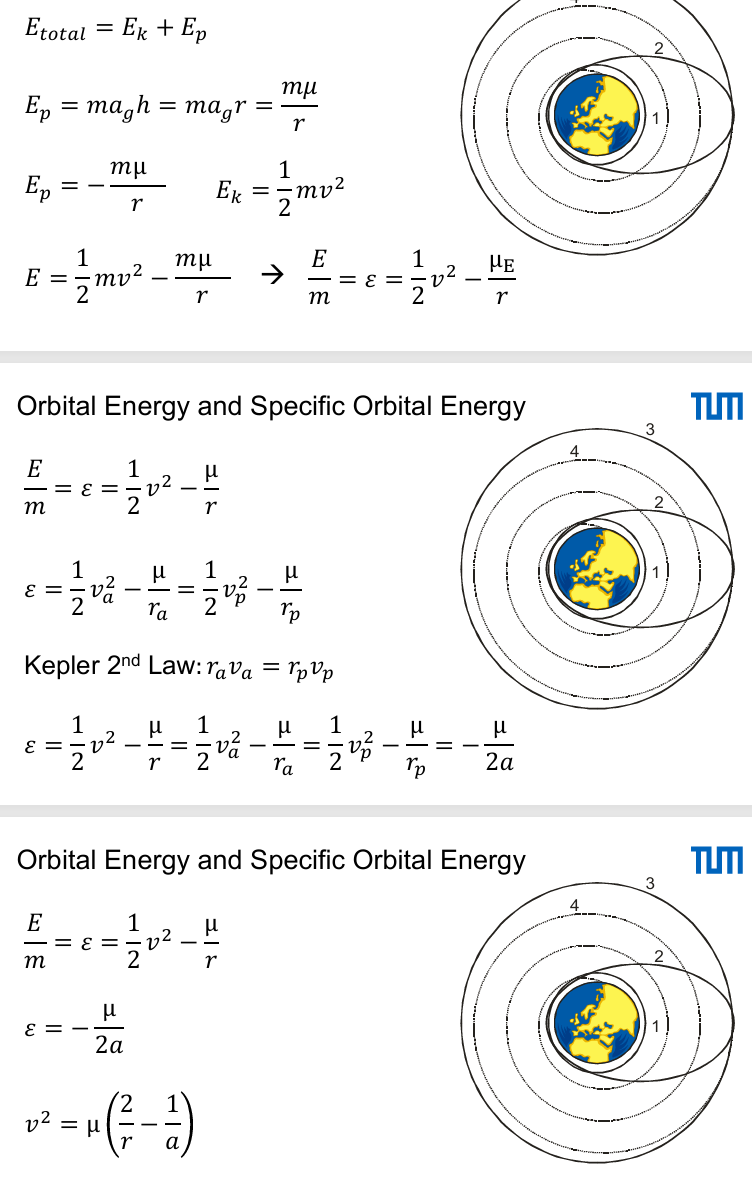
Orbital Engery

Kinetic Term E_k: Equilibrium centrifugal vs. centripetal (grav.) forces

Potential Term E_p: Work done in the gravitational field working against gravity

Gains und Losses Delta_E: Gravitational losses, aerodynamic losses energy needed for manoeuvres, orbit injection energy gained due to Earths rotation

Gravity is a conservative field, i.e. a field in which total energy is conserved

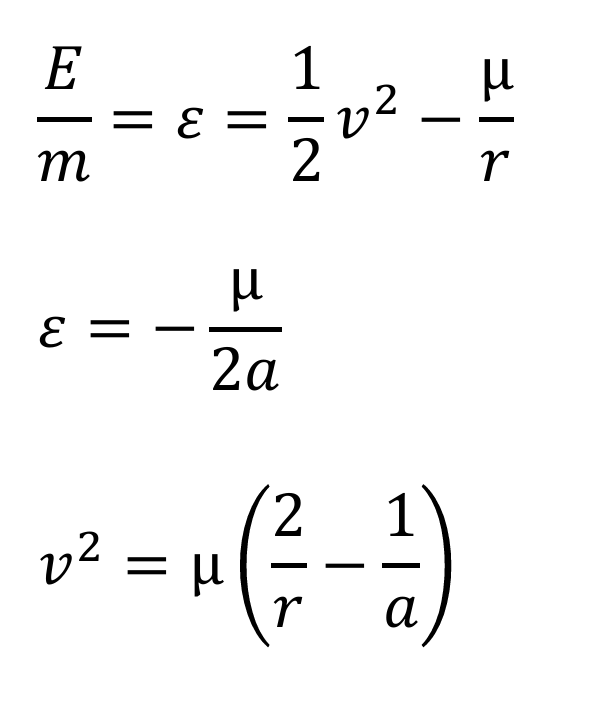
Practice: Derive the three equations in the image from the Orbital Energy Equation 

How can circular velocity of a body in circular orbit be defined ?

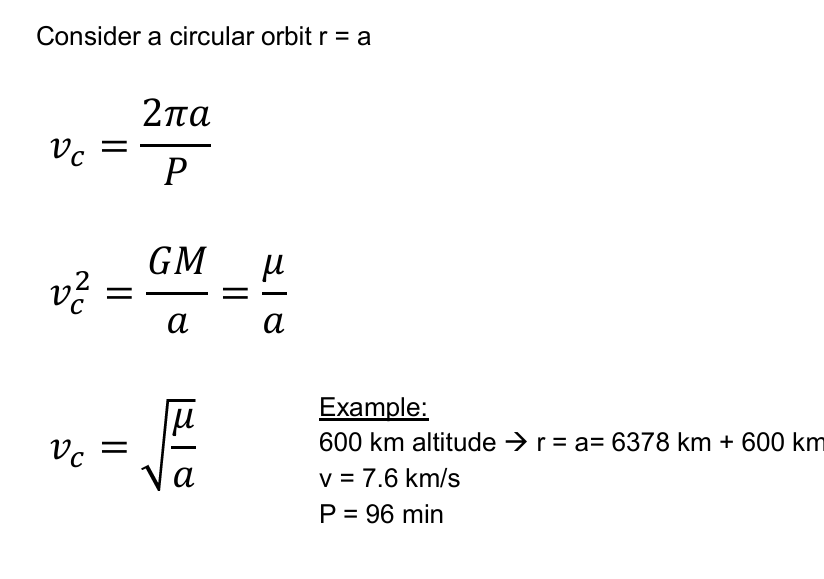
Specifical Orbital Energy

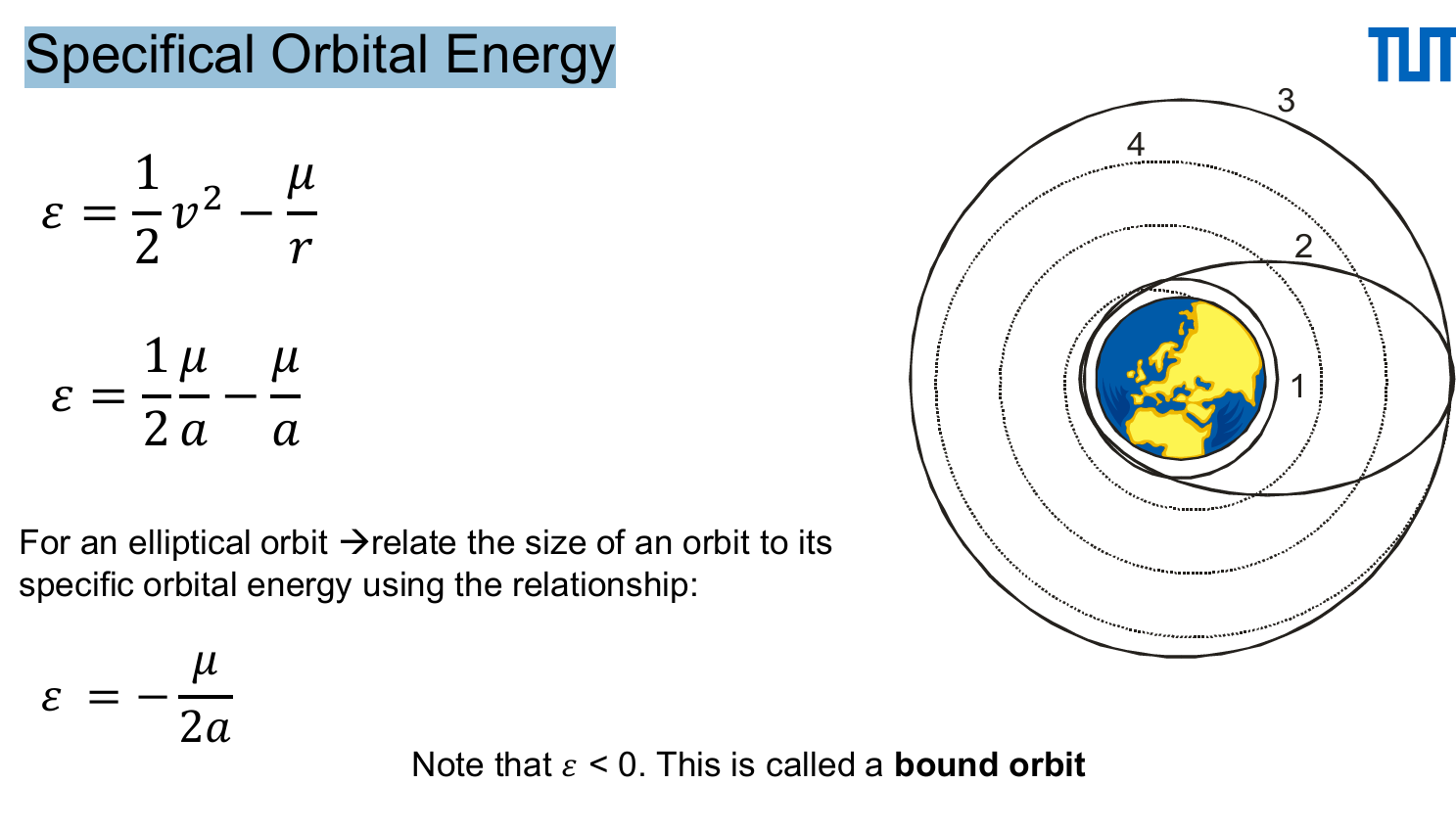
The Energy Law

• The specific orbital energy ε is the same at all points of the trajectory

• The total orbital energy per unit mass ε is the sum of the kinetic and potential energies per unit mass - vis-via energy

• For an “elliptic orbit”, the specific orbital energy is the negative of the additional energy required to accelerate a mass of one kilogram to escape velocity (parabolic orbit).

• For an “hyperbolic orbit”, the specific orbital energy is the excess energy compared to that of a parabolic orbit. In this case the specific orbital energy is also referred to as characteristic energy

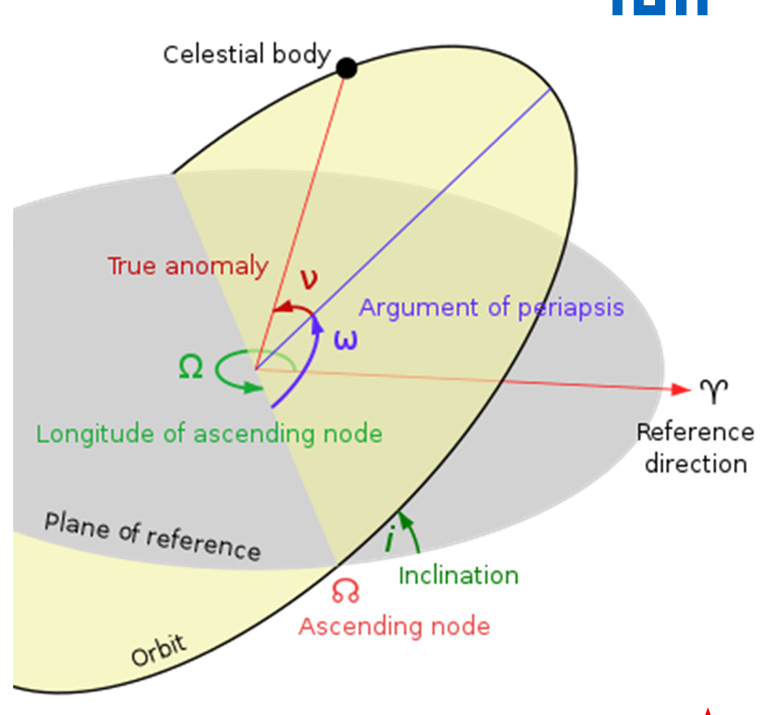
What are the six orbital elements to mathematically describe an orbit ?

• Orbital Size: Semi-Major Axis, a

• Orbital Shape: Eccentricity, e

• Orientation of the orbital plane in space

  • Inclination, i

  • Longitude of Ascending Node, Ω → Right Ascension of the Ascending Node (RAAN)

• Orientation of the orbit with the plane: Argument of Periapsis/Perigee, ω

• Object’s location in the orbit: True anomaly, υ

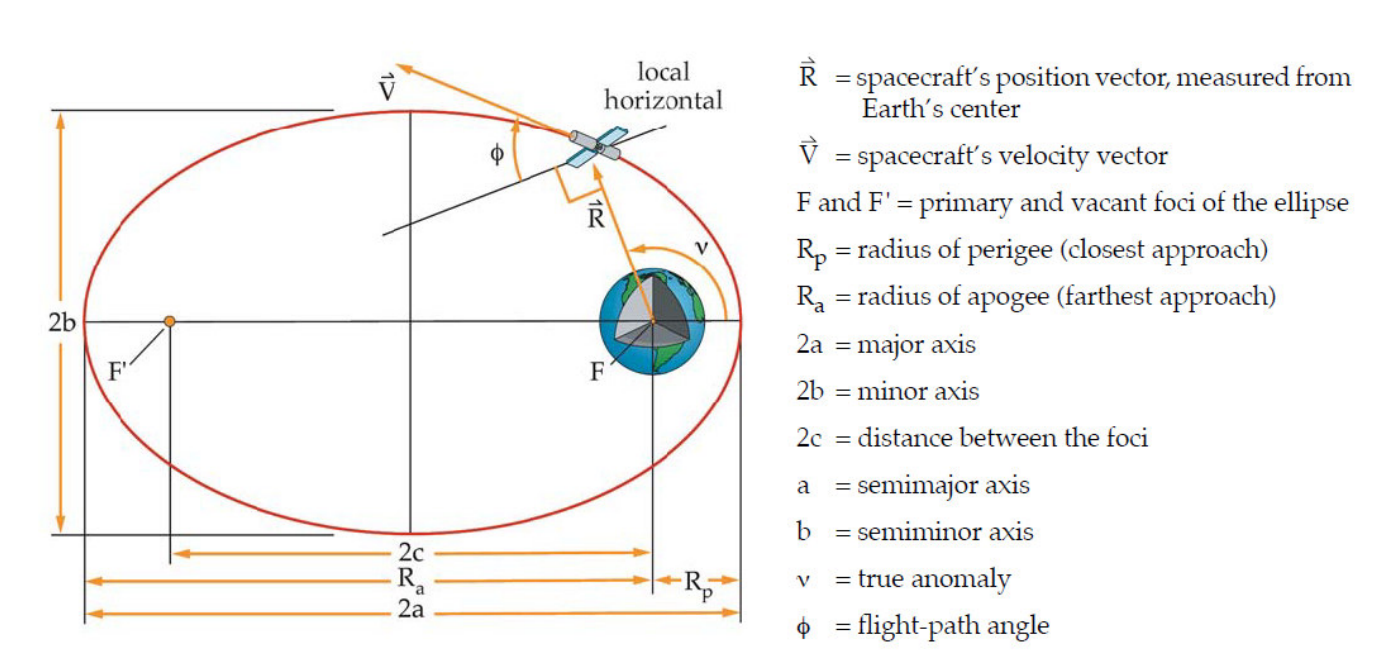
Semi-Major Axis a

Apoapsis: the point in an object's orbit where it is farthest from the celestial body it is orbiting

Periapsis: the point in an object's elliptical orbit where it is closest to the body it is orbiting

Focus: one of two special points that define an elliptical orbit, with the central body (like a star or planet) located at one of the foci, think of them as a center of orbit

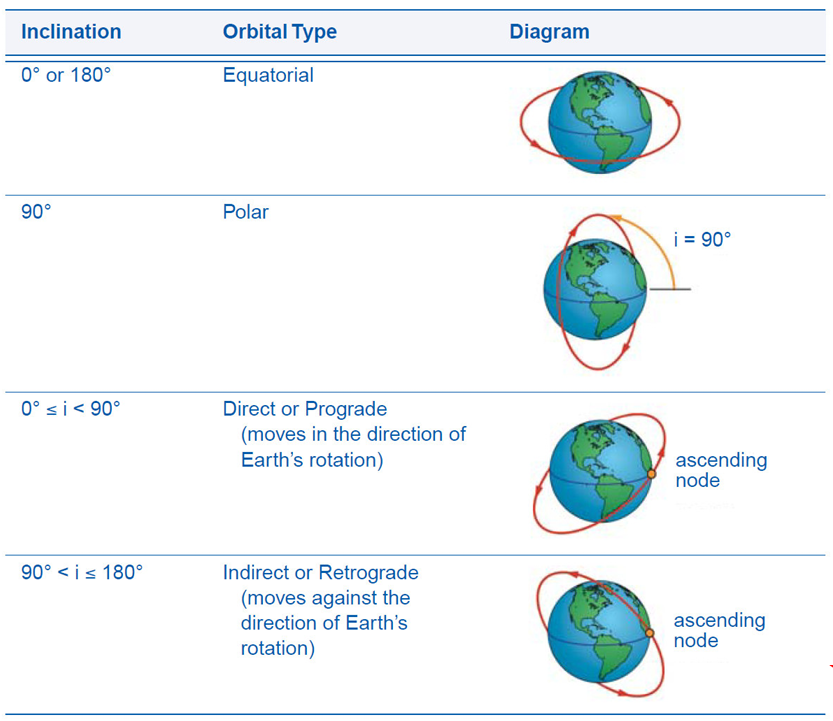
Inclination i

“ describes the tilt of the orbital plane with respect to the equator “

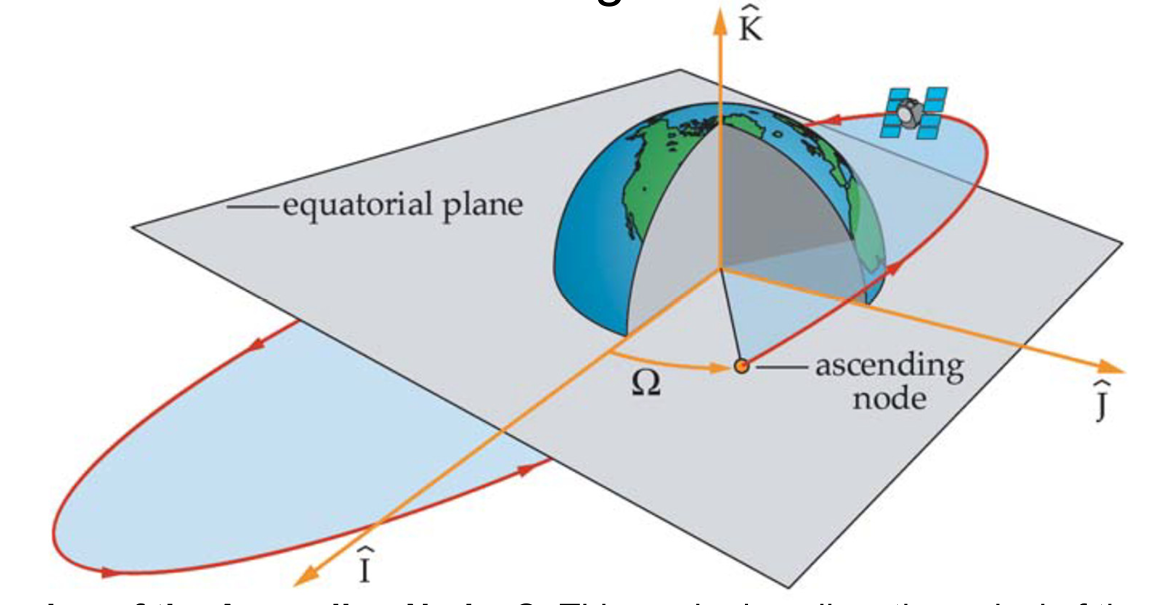
Right Ascension of the Ascending Node - RAAN

“It is the angle along the equator between the principal direction, I, and the point where the orbital plane crosses the equator from south to north (ascending node), measured eastward”

RAAN = Longitude of Ascending Node, Ω for Earth

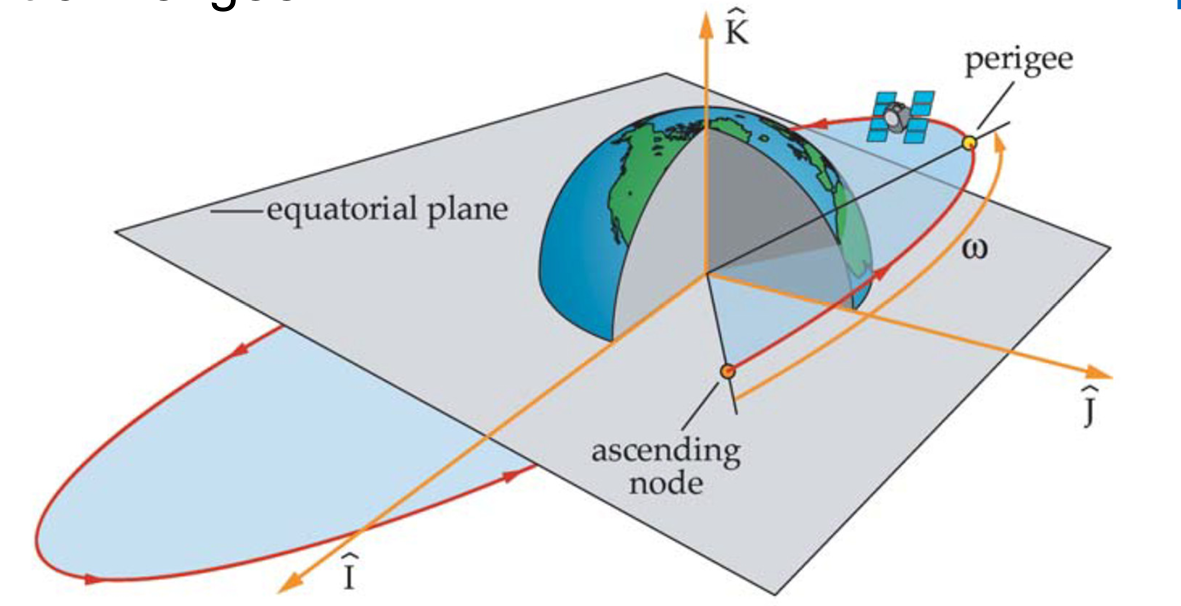
Argument of Perigee ω

“It is the angle between the ascending node and perigee, measured in the direction of the spacecraft’s motion”

pergiee: the point in the orbit of an object, such as a moon or a satellite, where it is closest to Earth. Specific term for periapsis when the orbit is around the Earth

True Anomaly υ

“It’s the location of a spacecraft within the orbit. It is the angle between perigee and the spacecraft’s position vector measured in the direction of the spacecraft’s motion”

Coordinate system. What is it and how do we classify it ?

“A coordinate system is a system that uses one or more numbers, or coordinates, to uniquely determine the position of the points or other geometric elements on a manifold such as Euclidean space. Euclidean space is the fundamental space of geometry, intended to represent physical space. “

Classification:

• Depending on the type of coordinate system:

  • Rectangular Coordinates

  • Polar Coordinates

  • Cylinder Coordinates

• Depending on the origin point of the coordinate system:

  • Heliocentric (Origin in the center of Sun)

  • Geocentric (Origin in the center of Earth)

  • Barycentric (Origin the center of gravity Planet-Sun or Planet-Moon)

  • Topocentric (Origin in the observation point)

• Depending on the position of the x-y- plane:

  • Ecliptical (x-y- Plane parallel to the ecliptic)

  • Equatorial (x-y-Plane parallel to the Earth equatorial plane)

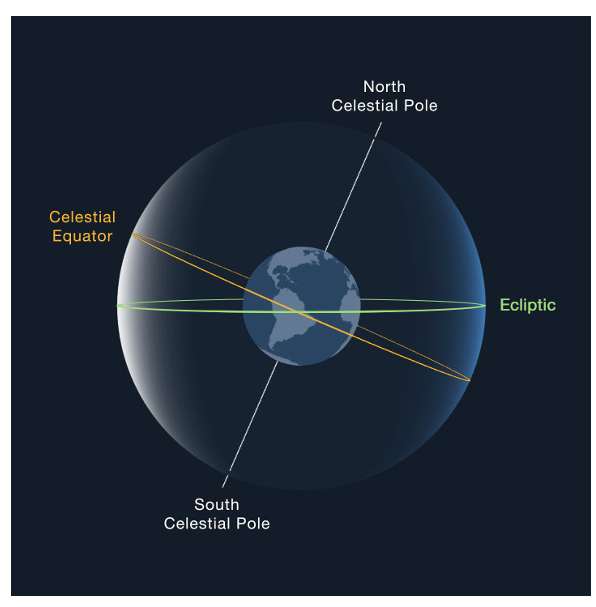
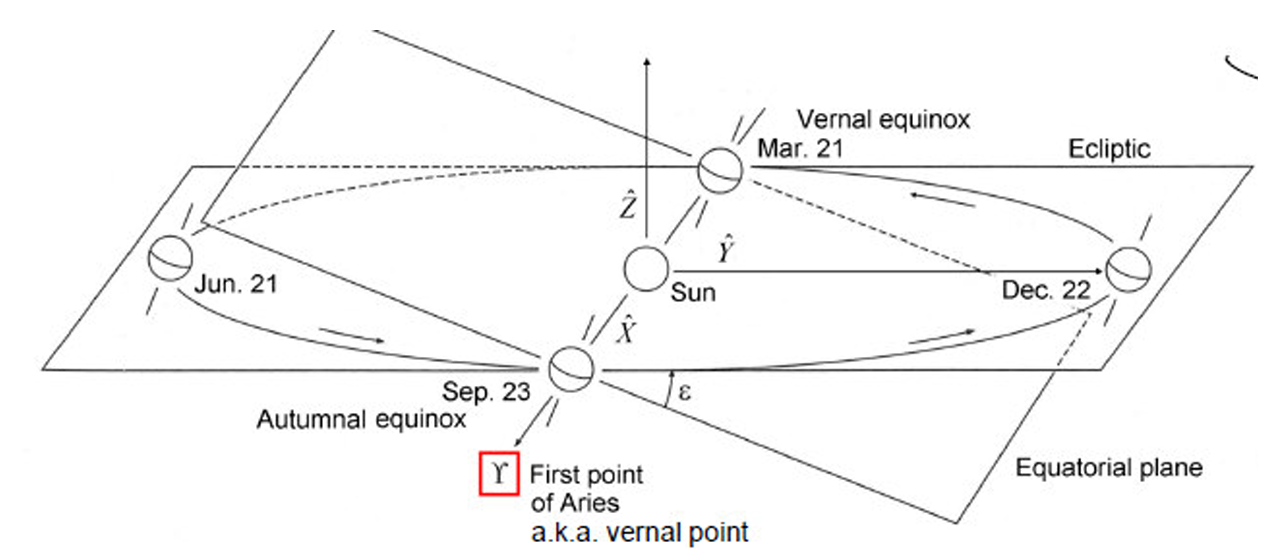
First Point of Aries Υ

“The point on the celestial sphere as seen from the Sun to the ascending node of the intersection between the terrestrial equatorial plane and the ecliptic, which equals the direction in which the Sun is seen from Earth at vernal equinox”

“It is shared by the equatorial and ecliptical coordinate system and is used in both to specify the direction of the x-axis.”

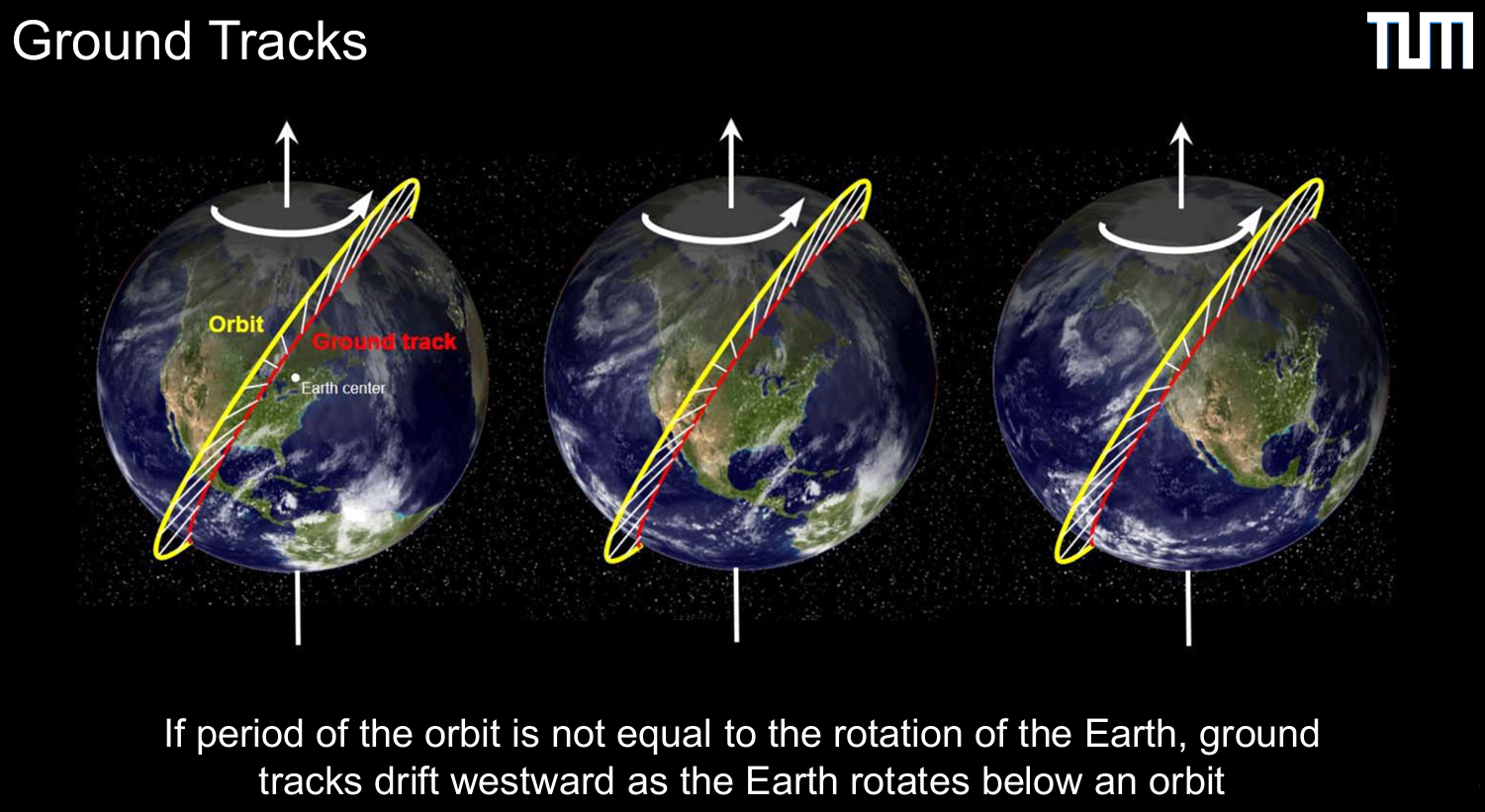
Ground Track

“A ground track or ground trace is the path on the surface of a planet directly below a satellite's trajectory”,

“vertical projection of the satellite's orbit onto the surface of the Earth”,

“In other words, the ground track is the set of points at which the satellite will pass directly overhead in the frame of reference of a ground observer”

Geosynchronous Orbit, GSO

• Circular orbits around the Earth having a period of 24 hours

• geosynchronous orbit + zero degree inclination = geostationary orbit, appears to hang motionless above one position on the Earth's equator. For this reason, they are ideal for some types of communication and meteorological satellites.