Circle formulas

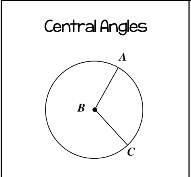
Central angle

Arc length=measure

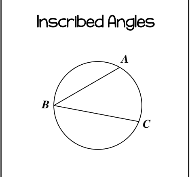
Inscribed angles

Arc length/2

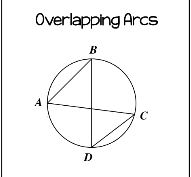
Overlapping arcs

m<ABD=m<ACD

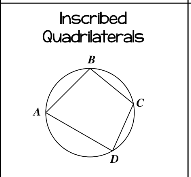
Inscribed Quadrilaterals

Opposite angles are supplementary

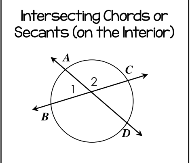
Intersecting chords or secant on the interior

m<1=(AB)+(CD)/2
m<2=(AC)+(BD)/2

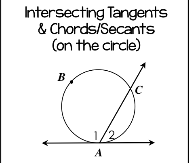
Intersecting tangents and chords/secants on the circle

m<1= major arc/2
m<2=minor arc/2

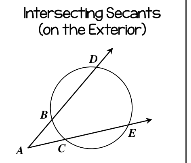
Intersecting secants on the exterior

big arc-small arc/2

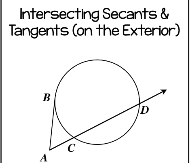
Intersecting secants and tangents on the exterior

big arc-small arc/2

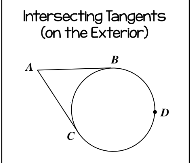
Intersecting Tangents on the exterior

Big arc-small arc/2

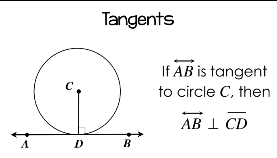
Tangents

Line AB is perpendicular to Segment CD

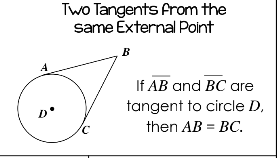
Two tangents from the same external point

The two tangents are congruent

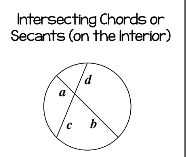
Intersecting chords or secants on the interior

part of chord*other part=part of chord*other part

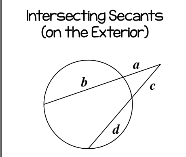
Intersecting secants on the exterior

outside*whole=outside*whole

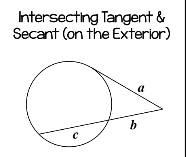
Intersecting tanget and secant on the exterior

tangent²=outside*whole

Area

A= πr²

Circumference

C = 2πr
C = πd

Arc Length

l= x*2πr/360

Standard Equation of a Circle

(x-h)²+(y-k)²=r²

Sector area

angle measure/360*πr²