AP Statistics All Units

Conditions for regression inference

L-Linear relationship

I- Independent observations

N- Normality of Residuals

E- Equal variance of Residuals

R- Random sample/eperiment

Confidence interval for slope

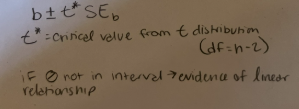
Hypothesis test for slope

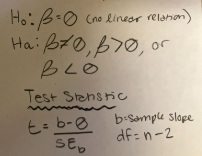
Confidence intervals for mean

Should be t star not z star

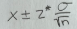
Confidence intervals for proportion

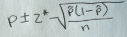
Hypothesis testing for means

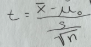
Hypothesis testing for proportions

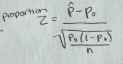
Normality conditions of means

n is greater than or equal to 30

Normality conditions of proportions

np is greater than or equal to 10

n(1-p) is greater than or equal to 10

Z-Tests

Use:

Parameter

Hypothesis

Assumptions and conditions

Name the test

T/o- Run the tests

M/s- Conclude

normal CDF

One sample

two sample

Matched Pairs

proportions

T-tests

Use:

Parameter

Hypothesis

Assumptions and conditions

Name the test

T/o- Run the tests

M/s- Conclude

tcdf

one sample

two sample

means

Z- Intervals

Use:

Parameter of interest

Assumptions and conditions

Name the test

I- find the interval

Conclude

proportions

one sample

two sample

t-intervals

Use:

Parameter of interest

Assumptions and conditions

Name the test

I- find the interval

Conclude

mean

one sample

two sample

Chi Squared Goodness of fit

correct or incorrect

Chi Squared test

Homogeneity- Different or not different

Independence- Association or no association

Central limit theorem CLT

if samples are large enough the sample mean/proportion distribution is approximately normal

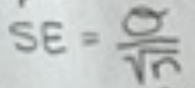
Sample means mean and standard deviation

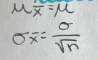
Sample proportion mean and standard deviation

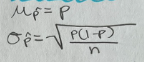
Z Score for sample means

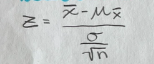
Z score for sample proportion

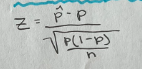
Confidence intervals

use sampling distributions to estimate population parameters PANIC

Hypothesis tests

use sampling distributions for calculating test statistics and p-values PHANTOMS

Random variable

a value outcome from a random process

discrete

finite/countable number of values

continuous

all values in an interval

Probabilitiy distributions

lists values of a random variable and their probabilities

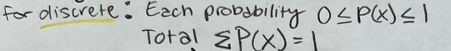
Standard deviation

spread

combining random variables

for independent x and y

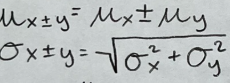
Binomial distributions

Binary

Independent

Number- fixed number of trials n

Success(same p)

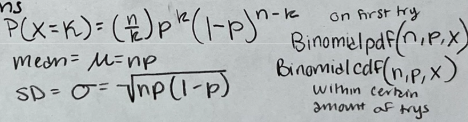
Geometric Distributions

trials until first success

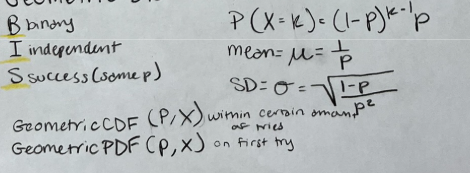
Conditional probability

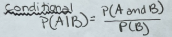
Independence with probability

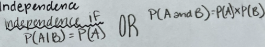
Two-way tables and venn diagrams

useful for calculation joint, marginal and conditional probabilities

helpful visuals for understanding overlap and independence

General multiplication rule for probability

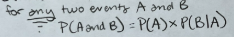
Tree diagrams

useful to model multi stage processes

helps visualize and compute compound probabilities

using probability to make a decision

expected value and risk assessment

Probability

long run frequency of an event

0=impossible

1=certain

Complement rule

probability that event A doesn’t happen

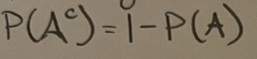
Addition rule

OR- if A and B are mutually exclusive

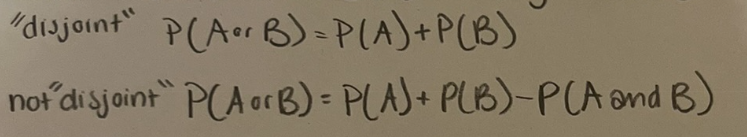
Multiplication rule

AND- if A and B are indepedent

P(AandB)=P(A)xP(B)

Independence

one event doesn’t affect the other

ex. flipping a coin

Disjoint

mutually exclusive

can’t happen at the same time

ex. rolling a die and getting a 2 and a 3

Simulation steps

describe a process, assign digits to outcomes, preform trials, record outcomes, repeat enough trials for accurarcy, use results to estimate probability

Observational study

no treatment applied;observed objects as they are

Experiments

imposes treatment to measure cause and effect

population

entire group you want to study

sample

subgroup of population

census

data from every member of population

sampling frame

list of individuals where a sample is drawn

Simple random sample

every individual has an equal chance of getting selected

Stratified random sample

divide into strata, then randomly select within each

cluster sample

divide into clusters, randomly select whole clusters

systematic sampling

every #th individual

convinence sample

easy reach but strong likeihood of bias

voluntary sample

people choose to respond often biased

Undercoverage bias

some groups are not represented

nonresponse bias

people don’t respond

response bias

influenced by wording, interviewer, or lying

sampling bias

favors certain outcomes

Principals of designing a study

control

replication

random assignment

comparison

Completely randomized experimental design

subjects randomly assigned to treatments

randomized block experimental design

subjects break into groups, then randomly assigned

matched pairs experimental design

each subject gets both treatments, or paired with similar individuals

Confounding variable

influences both dependent and independent variables

lurking variable

not included in study but affects interpretation

Percentiles

value below which a given percentage of data falls

z-score

how many standard deviations a value is from the mean

positive z score, greater than mean

negative z score, less than mean

Adding and subtracting a constant

impacts center(mean and median)

DOESN’T impact shape or spread(IQR and SD)

Multiplying and dividing by a constant

impacts center and spread

DOESN’T impact shape

Using Normal distributions

normalcdf(lower value, upper value, mean, standard deviation)

invnorm(area, mean, standard deviation)

Quantitative

measureable numbers

qualitative

categorical and groups

Bar graph

categorical data, bars don’t touch

Histograms

quantitative data, bars touch

Dot plots

small data sets

box plots

summarize data using min, max, Q1, Q3, and median

Outlier rule for box plots

Q3+IQR(1.5)

Q1-IQR(1.5)

Symmetrical

both sides are equal

Uniform

even distribution

Empurical Rule

68% of data is within 1 standard deviation of the mean

95% of the data is within 2 standard deviations of the mean

99% of the data is within 3 standard deviations of the mean