elastic potential energy

what is energy in the elastic potential store of an object is defined as?

the energy stored in an elastic object when work is done on the object

how can objects change shape?

This means that any object that can change shape by stretching, bending or compressing (eg. springs, rubber bands)

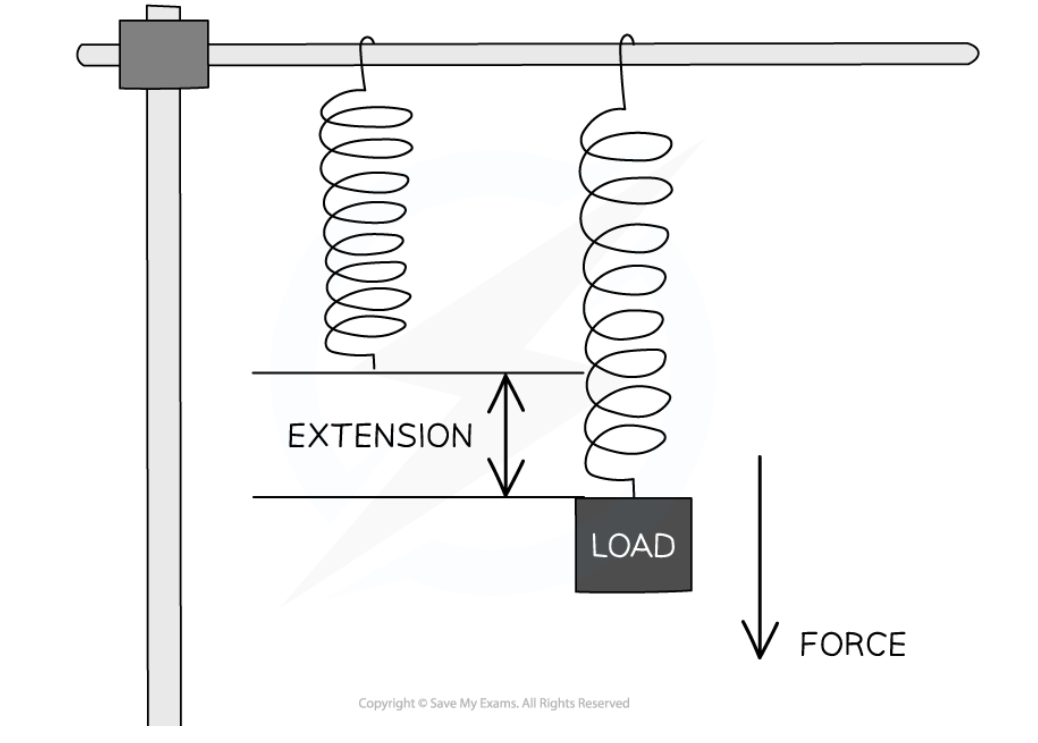
what happens when spring is stretched or compressed?

When a spring is stretched (or compressed), work is done on the spring which results in energy being transferred to the elastic potential store of the spring

what happens when spring is released?

When the spring is released, energy is transferred away from its elastic potential store

how do you calculate elastic potential energy?

Ee = ½ × k × e2

elastic potential energy = ½ x spring constant x extension

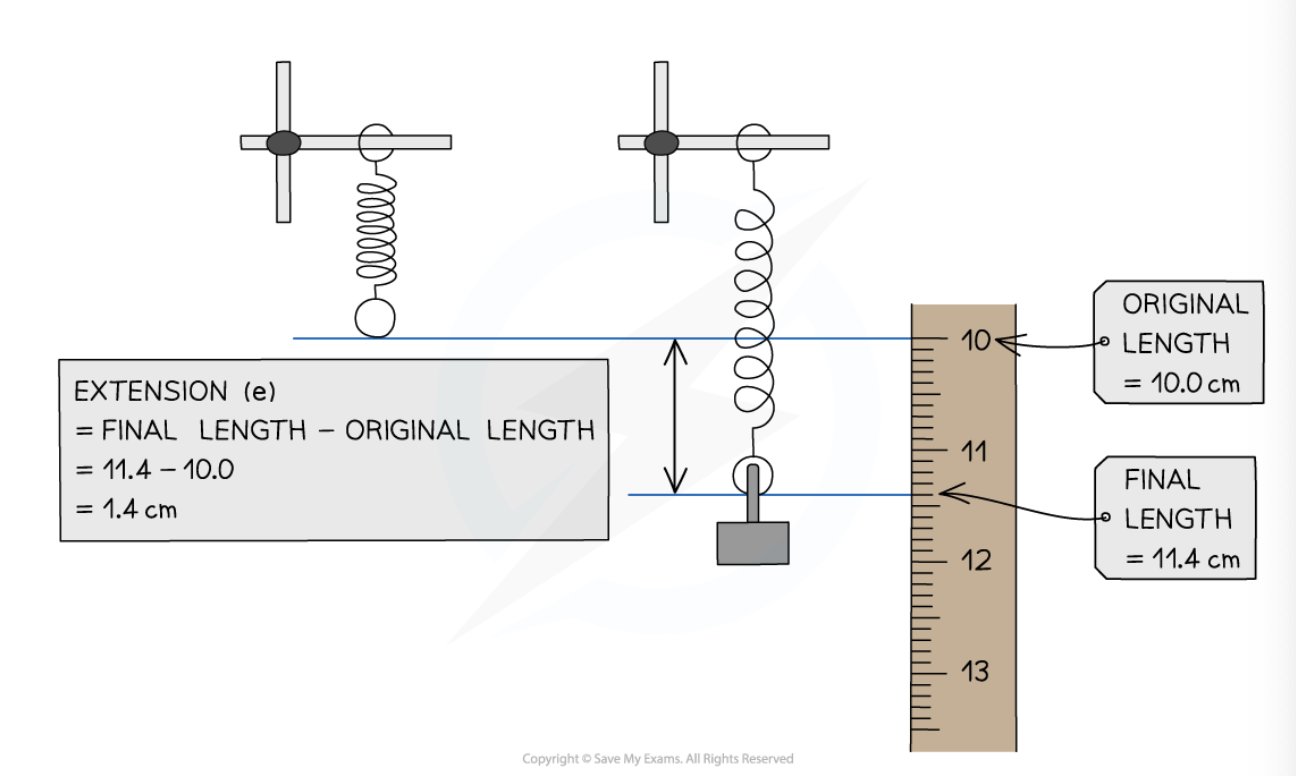
A mass is attached to the bottom of a hanging spring with a spring constant of 250 N/m. It stretches from 10.0 cm to 11.4 cm.

Calculate the elastic energy stored by the stretched spring.

Step 1: Determine the extension of the spring

Step 2: List the known quantities

• Spring constant, k = 250 N/m

• Extension, e = 1.4 cm = 0.014 m

Step 3: Write out the elastic potential energy equation

Ee = ½ ke2

Step 4: Calculate the elastic potential energy

Ee = ½ × 250 × (0.014)2

Ee= 0.0245 J

Step 5: Round the answer to 2 significant figures

Ee = 0.025 J