ap physics c electrostatics & potential - january 2026

e

1.6 × 10^-19

k

9 × 10⁹

ε_o

8.85 × 10^-12

electric flux

φ = EAcosθ = Q_enc/ε_o

charge densities

ρ = Q/Volume

σ = Q/Area

λ = Q/Length

V due to multiple charges

k ∑ q/r

U due to multiple charges

k ∑ q₁q₂/r₁₂

U of a system

W needed to bring in charges from ∞

k ∑ q₁q₂/r₁₂ but for all charges with each other

V for point near finite line

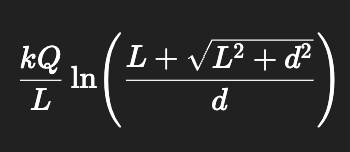
if point P is the perpendicular bisector of the line, treat each half as a separate finite line and then add the results

where L is the length of the finite line and d is the distance of the point to the line

V for point near a disc of charge

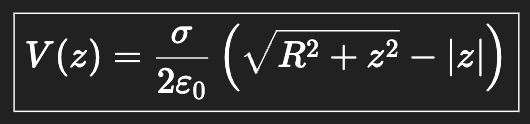
process for solving for V of a distribution of charge

V = ∫kdq/r

figure out dq using the charge density

figure out r using the location of the test charge

using bounds, solve the integral

calculating E from V

E = -∇ V

V of a charged conductor

constant inside & equal to the V on its surface

E is 0 inside, so no work is required to move a charge inside

ΔV is 0 going from the surface of a conductor to a point inside a conductor, as well as between any points two inside a conductor

the graph of V over r depends on the geometry of the conductor

for a sphere or point charge, the graph will be V∝1/r after R

two charged conductors connected with a metal wire

final V of both conductors become equal to one another

use kq/r = kQ/r & conservation q+Q=q+Q

ΔV near infinite line of charge

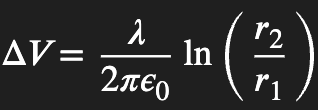
really easy to solve for just knowing E

ΔV near insulating plane

σ/2ε (r_b-r_a)

ΔV near insulating cylinder

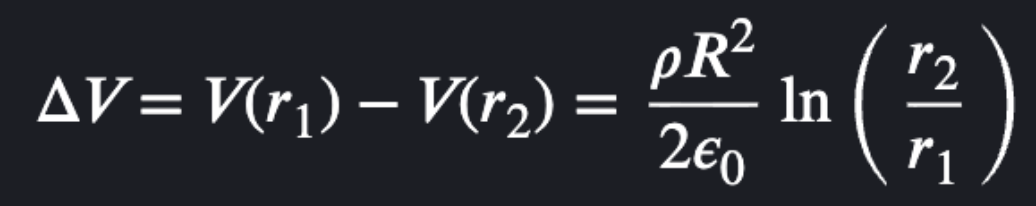
V inside insulating sphere

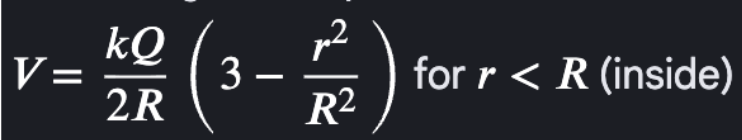
V outside sphere

same as point charge

area & volume of a sphere

A = 4πR²

V = (4/3)πR³

area & volume of a cylinder

A = 2πRL (main) + 2πR²

V = πR²L

ρ & λ of a cylinder

Q = ρ(πR²L)

λ=Q/L=ρπR²

E inside of a conductor

= 0

Disjointed E

With an off-center charge (+Q) inside of a hollow conductor, the (-Q) on the inner surface will be off-center.

However, +Q on the outside surface will be evenly distributed.

There is no communication between the inside & outside surfaces of a hollow conductor.

E due to an infinite line of charge

E = λ/2πε_or

E due to an infinite insulating flat sheet

E = σ/2ε_o

E due to an infinite conducting flat sheet

E = σ/ε_o

twice as big because the charges are more concentrated

E due to two parallel infinite insulating sheets

E_net = σ₁/2ε_o (ř₁) + σ₂/2ε_o (ř₂) → basically just adding up the Es

in the middle: E₁-E₂

on the right or left: E₁+E₂

E due to two parallel infinite conducting sheets

inside charges are equal & opposite

outside charges are equal

E between plates = |(q₁-q₂)/2| / Aε_o

E outside plates = |(q₁+q₂)/2| / Aε_o

E inside an insulating sphere

E = ρr/3ε_o = kQr/R³

E outside a sphere

same as point charge

E inside an insulating cylinder

E = ρr/2ε_o

E outside of a cylinder

ΔU =

= -W

=-∫F⋅dr

= kqQ/r

= q_tΔV

E =

E = F/q

= kQ/r²

= ∫k*dq/r²

F =

(newton’s second law)

F = qE = ma

or Coulomb’s law

ΔV

ΔV

= ΔU​/q

= -∫E⋅dr = V(B)-V(A) with the bounds of the integral being A on the bottom and B on top

= ∫k*dq/r​

= kQ/r (for point charge or outside a spherically symmetric charge)

work done by E

W

= ∫F•dr

= q∫E•dr

= -qΔV

=-ΔU

U depending on charge

like charges → U>0

opposite charges → U<0

so if you move positive charge against electric field or move a negative charge with the electric field ΔU>0

F_E compared to F_G

F_E is much stronger than F_G

Electric dipole

Two equal but opposite charges (Q_net = 0)

Electric field goes from…

higher potential (more positive) to lower potential (more negative)

Higher potential means a more ____ charge

positive

Units for U_E & V

U_E can be Joules, Volt-Coulombs, Newton-Meters

V can be Volts, Newton-Meters/Coulomb

Why can’t same-sign charges produce a zero potential point (finite)?

Both have the same sign, so they cannot cancel

For opposite charges, where is V=0 located relative to the charges?

Closer to the smaller magnitude charge

How to find field from potential graphically?

Slope of V(x) is -E(x)

E=-dV/dx

E inside a metallic shell?

0

Approximating using a point with a distance from the object that is very small compared to the length of the object

Treat the object as infinitely long

Electrostatic induction

bringing a charged object next to a conductor attracts electrons from the object

What is the place where the force in the +x direction for a + charge is maximized on a V vs. X graph?

Where the slope of V has a negative value with the greatest magnitude

Where is the force zero on a V vs. X graph?

Where the slope of the potential curve is zero

What regions are positive charges attracted to?

Regions of lower potential!

How do you draw E using equipotential lines

Know that the electric field is always perpendicular to equipotential lines & the electric field points from higher to lower potential

Stuff about enclosed charge and flux

If the enclosed charge is zero, the net flux must be zero (but the field at every point along the surface doesn’t have to be zero because it could be positive at some locations and negative along others).

If the electric flux is zero, the net charge must be zero. (Could still have charge!)

Charge outside the Gaussian surface does not affect the net electric flux but it does affect the field along it.

W =

-delta U

½ mv² =

-delta U

work done by an electric field

q delta V

Three spheres with different charge density distributions but the same charge

Field & potential is identical outside the spheres

The closer the charge is to the center of the sphere, the greater the potential is at the center of the sphere.

For a particle to escape to infinity

The particle must have at least zero total energy

KE = qV = 1/2mv²

(Q)(Q/4piepsilon0a) = 1/2mv²

The charge is all the same distance from the point

Just do kq/r

What are equipotential lines?

Lines perpendicular to the electric field lines, where the electric potential is the same anywhere on the line.

No work is done when moving between points on an equipotential line.

E between 2 parallel charged plates

Ed = V_AB