Calc AB 25-26

need to memorize

Definition of Continuity

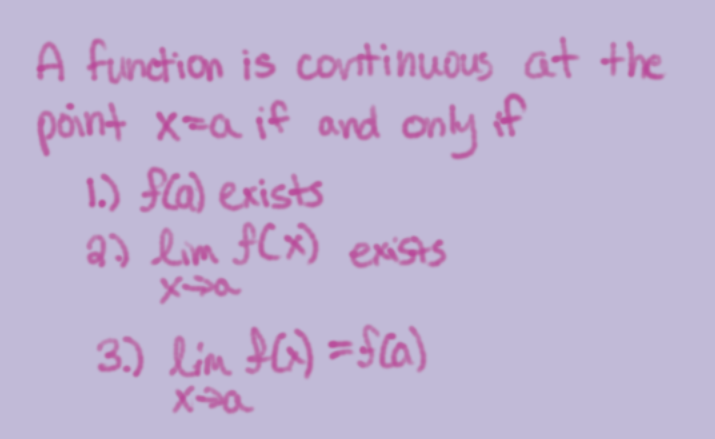
Intermediate Value Theorem (IVT)

Since f(x) is continuous on [a,b] and f(a)=__ and f(b)=__, there exists a value c such that f(c)=__ because f(a)<f(c)<f(b)

Limit Definition of a Derivative

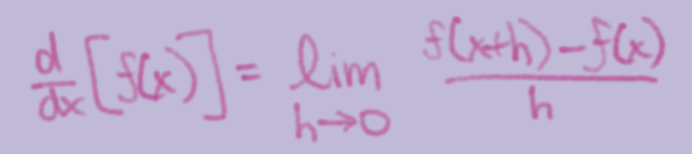
Meaning of a Derivative

At t=__, “the meaning of the function” is increasing/decreasing at a rate of __ units.

Extreme Value Theorem (EVT)

If f(x) is continuous over [a,b], there must be an absolute minimum and maximum on [a,b]

Not Differentiable

1.) discontinuous 2.) cusp/corner 3.) vertical tangent

Special Limit for sinx

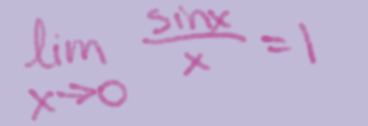
Special Limit for cosx

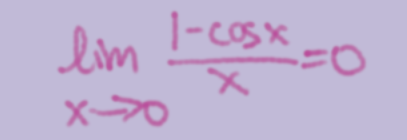
Power Rule

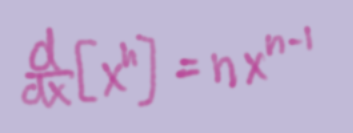
d/dx(sinx)

cosx

d/dx(cosx)

-sinx

d/dx(tanx)

sec²x

d/dx(cotx)

-csc²x

d/dx(secx)

secxtanx

d/dx(cscx)

-cscxcotx

d/dx(lnx)

1/x

d/dx(e^x)

e^x

d/dx(sin^-1x)

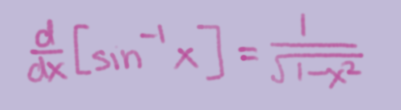
d/dx(cos^-1x)

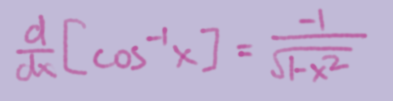
d/dx(tan^-1x)

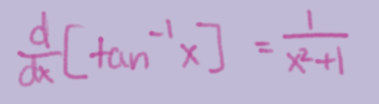
d/dx(cot^-1x)

-1/(x²+1)

Product Rule

d/dx(uv) = uv’ + vu’

Quotient Rule

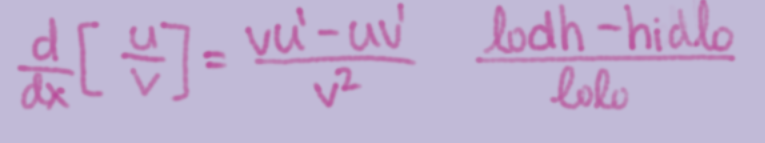
Chain Rule

d/dx[f(u)] = f’(u) * u’

Critical Points

f’(x)=0 or undefined

Relative Min/Max #1

min: f’(x) switches from negative to positive

max: f’(x) switches from positive to negative

L’Hospital’s Rule

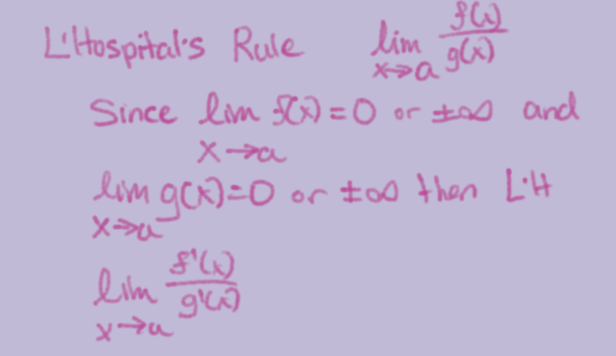
Mean Value Theorem (MVT)