AP Calculus AB Memory Test

f(x)=x²

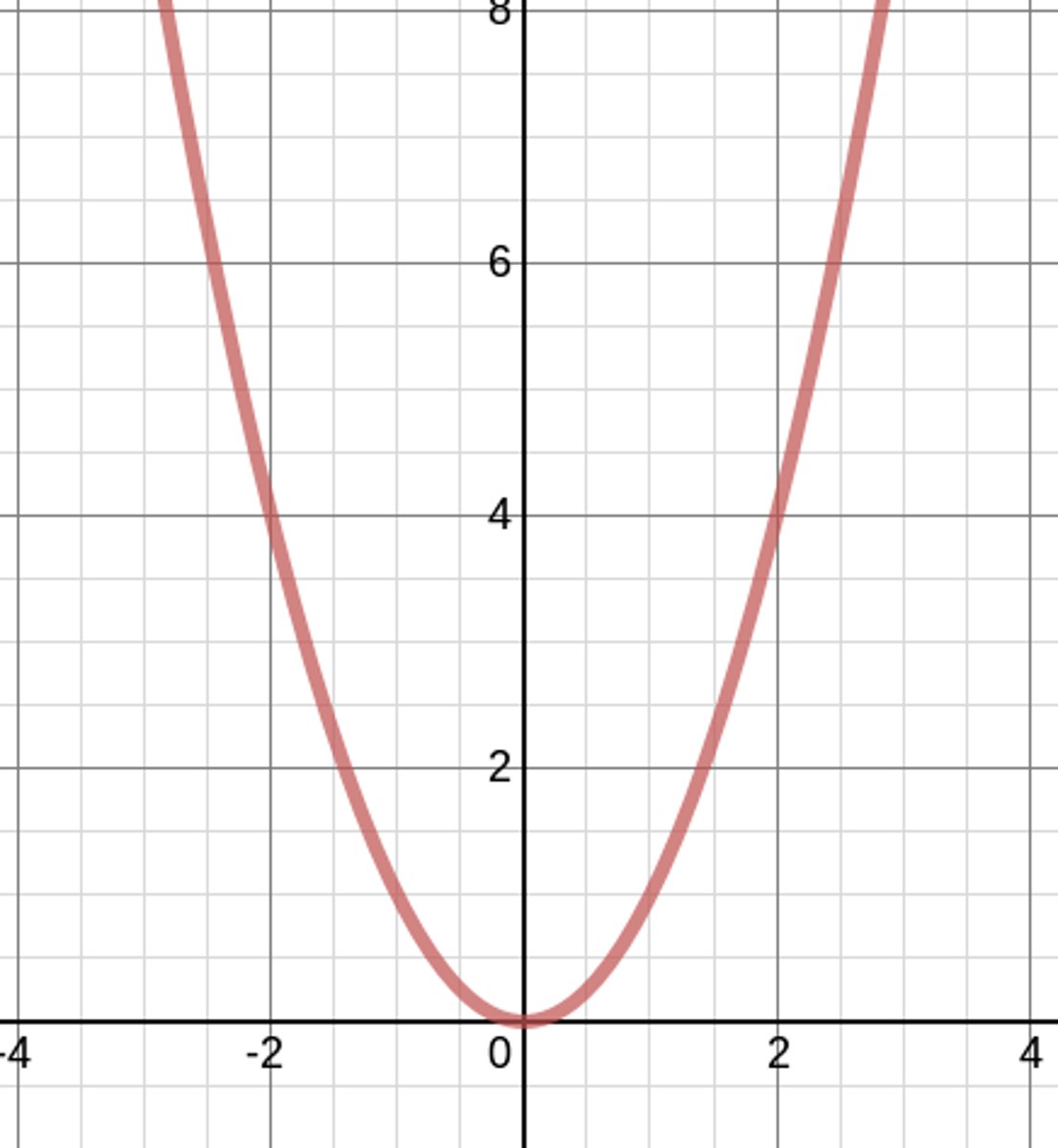
f(x)=x³

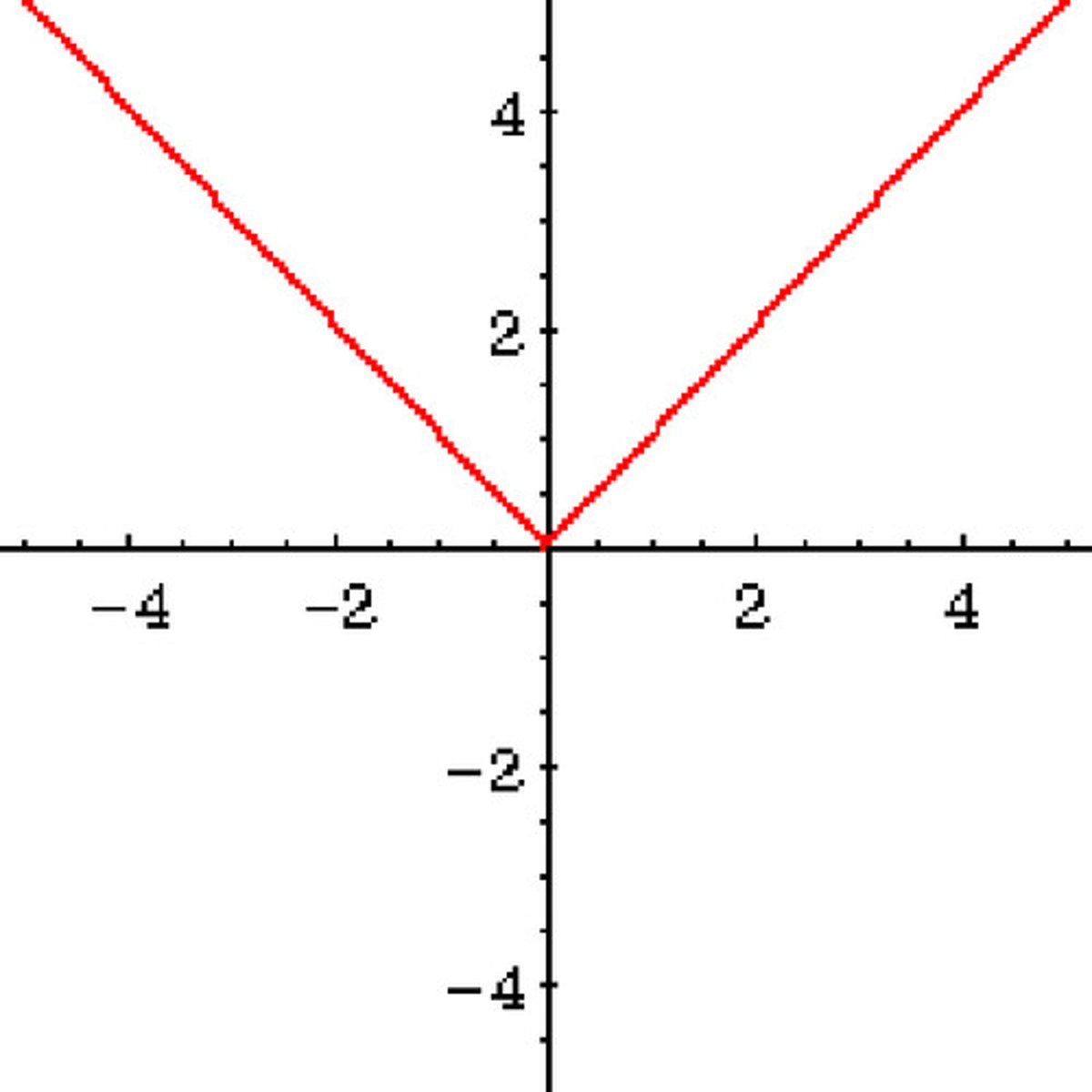
f(x)=|x|

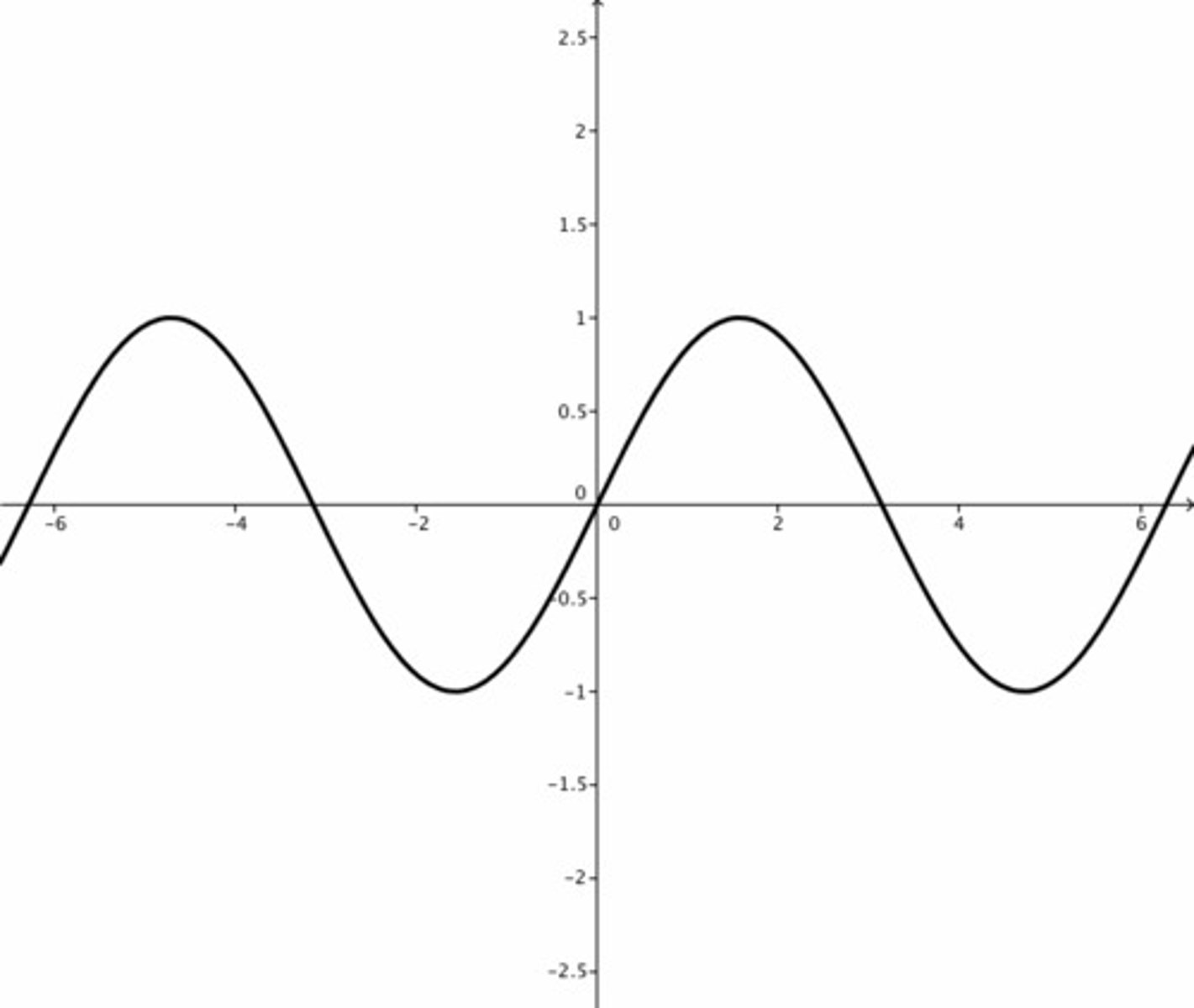
f(x)=sin(x)

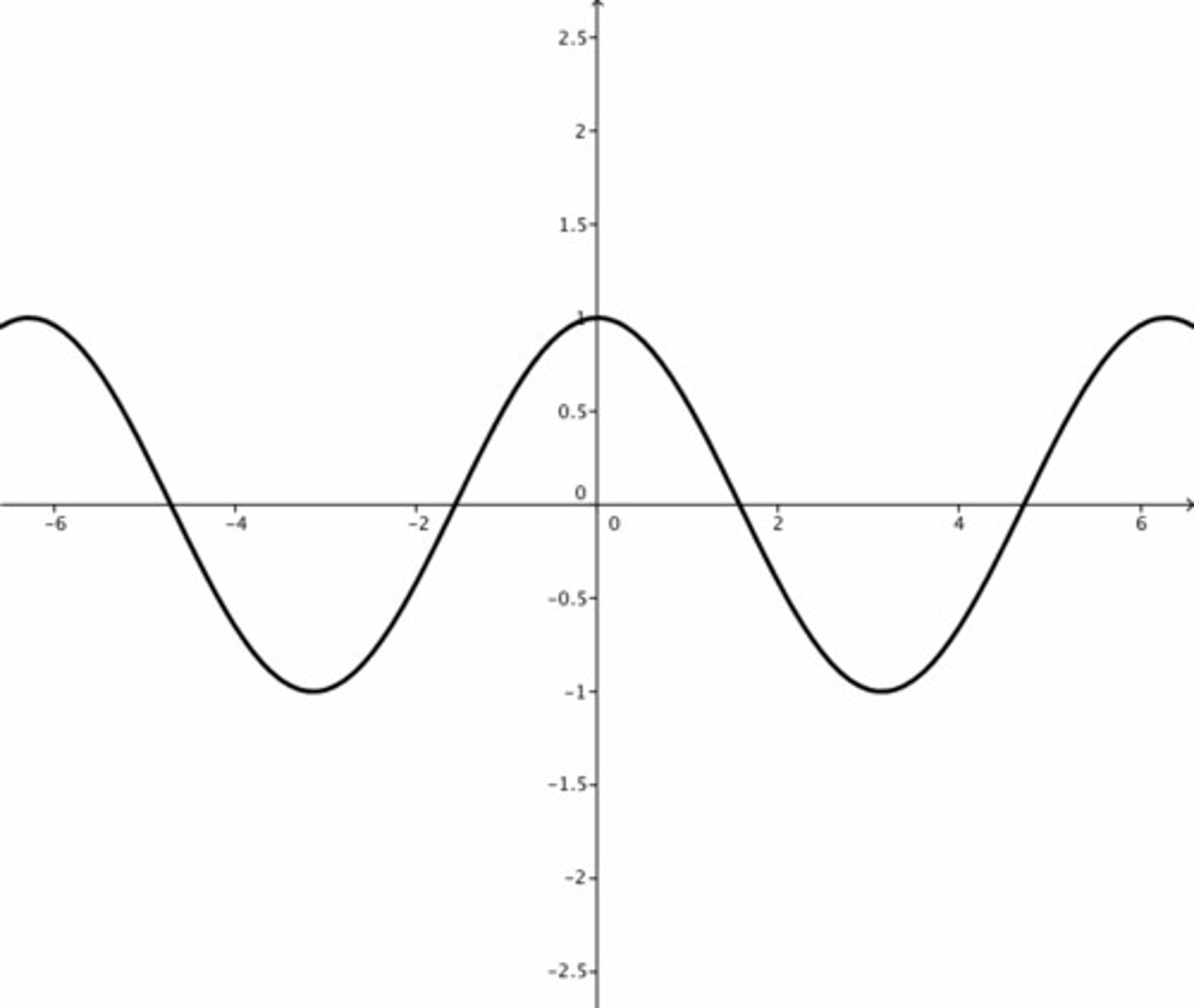
f(x)=cos(x)

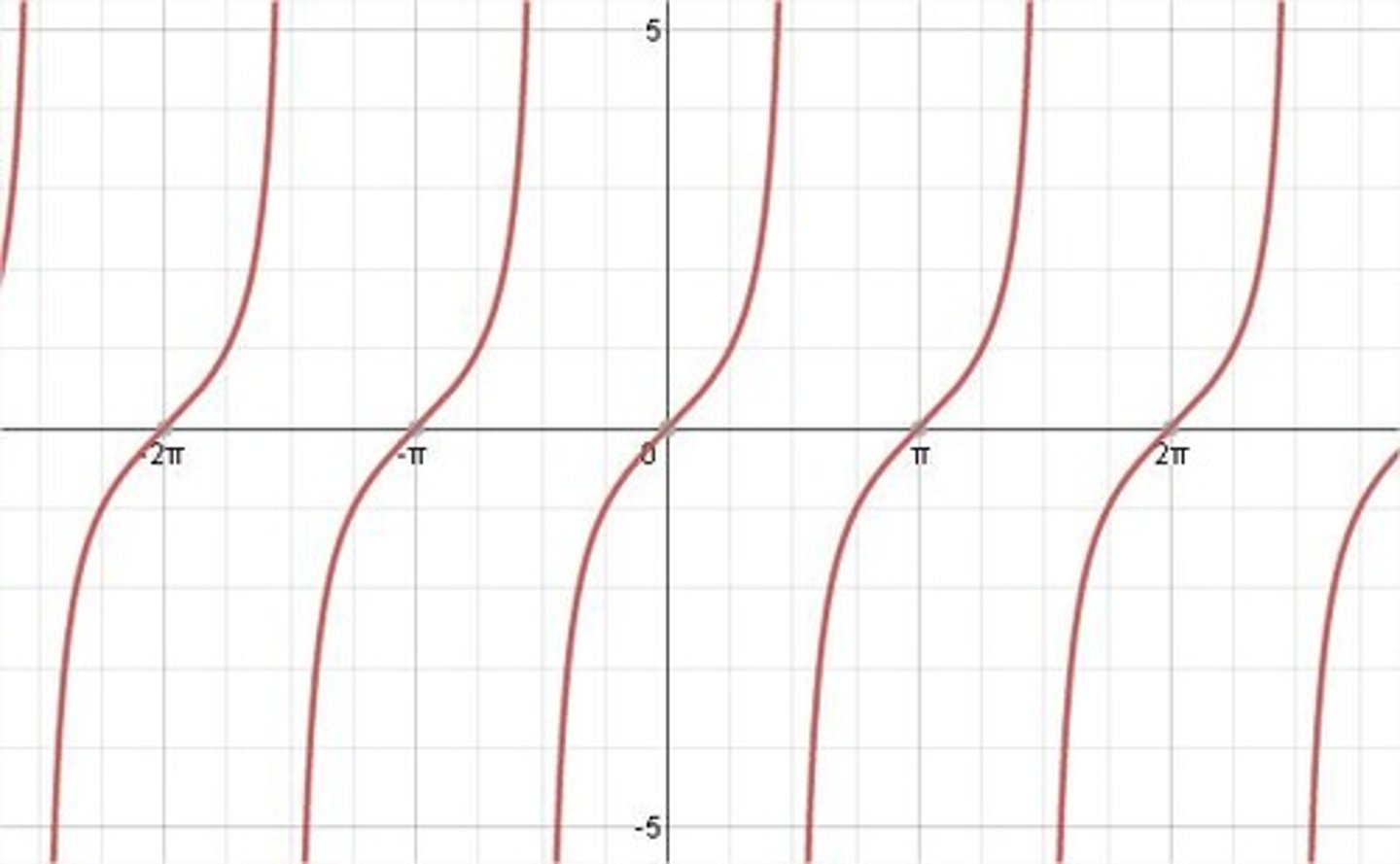
f(x)=tan(x)

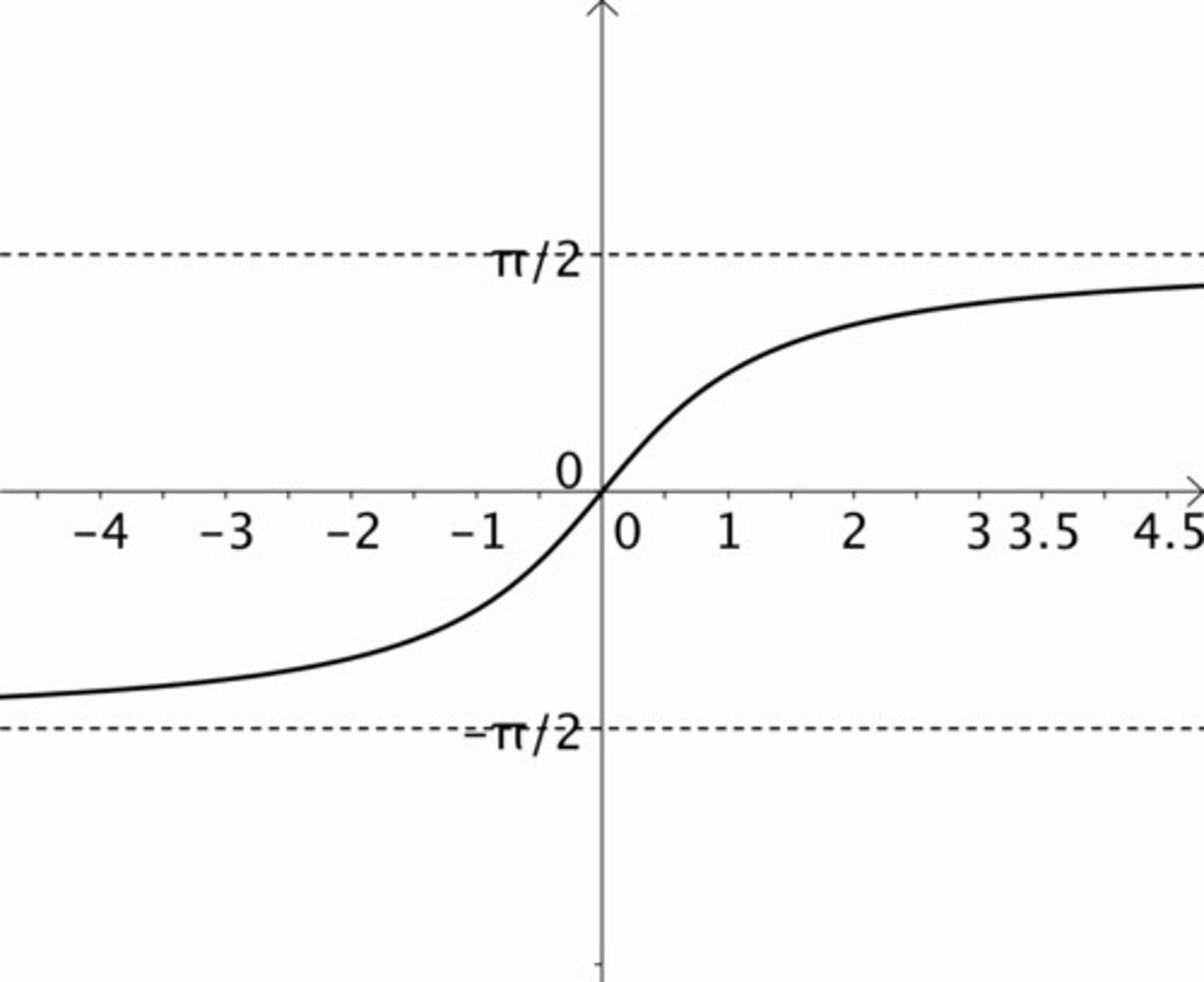
f(x)=arctan(x)

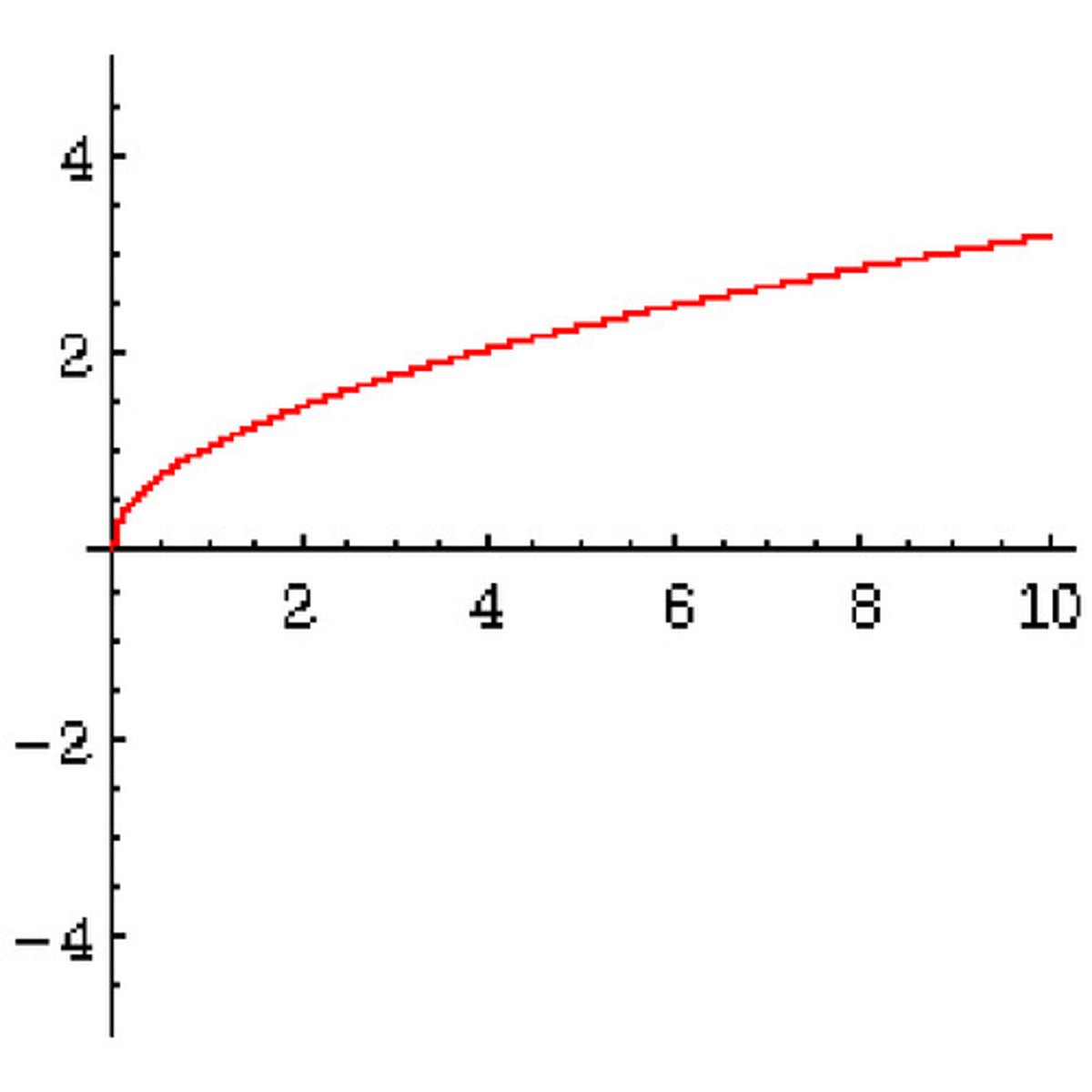
f(x)=√(x)

f(x)=√a²-x²

semi-circle graph (couldn't find image)

f(x)=e^x

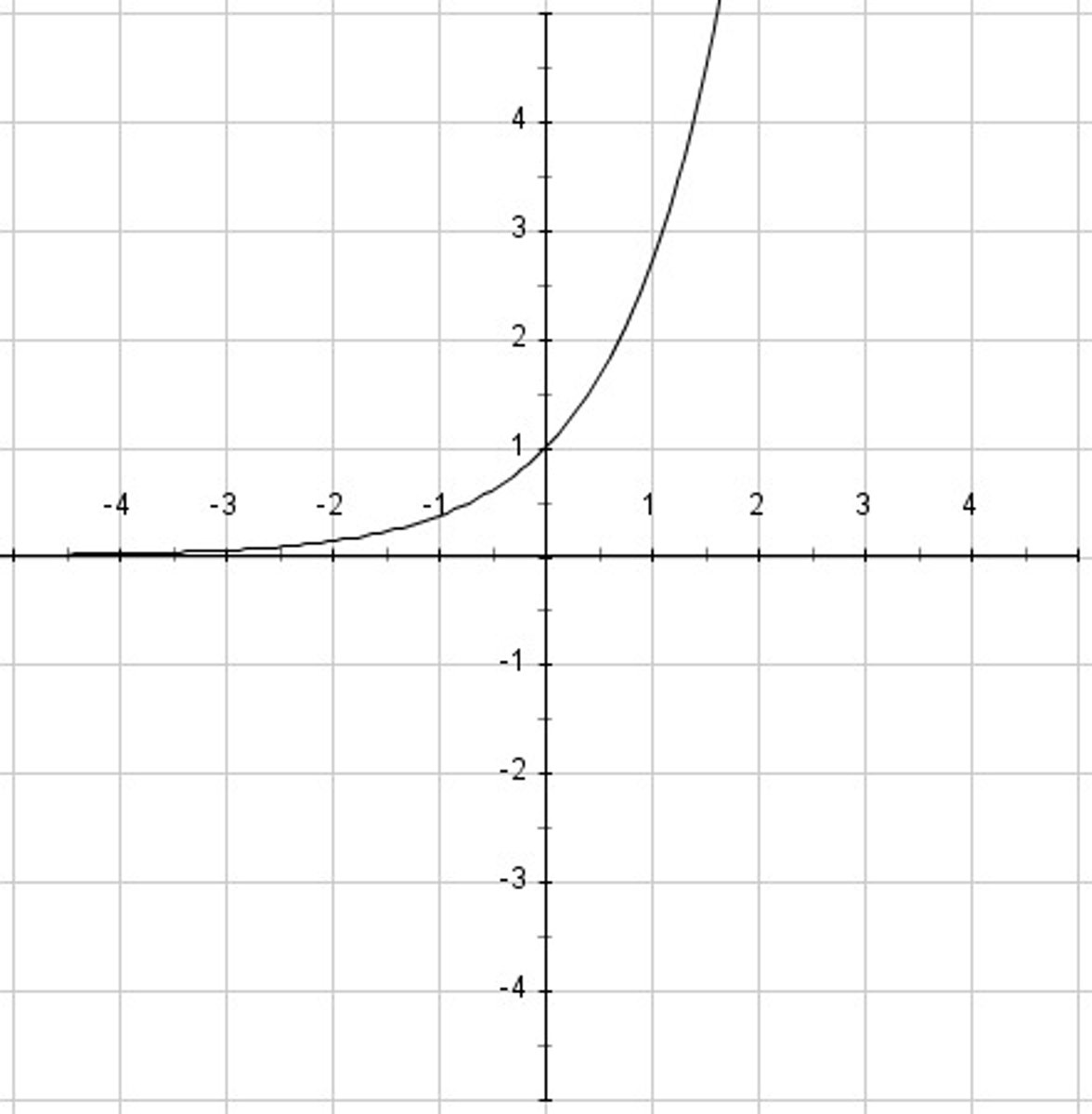
f(x)=e^-x

reflection of f(x)=e^x across the y-axis (couldn't find image)

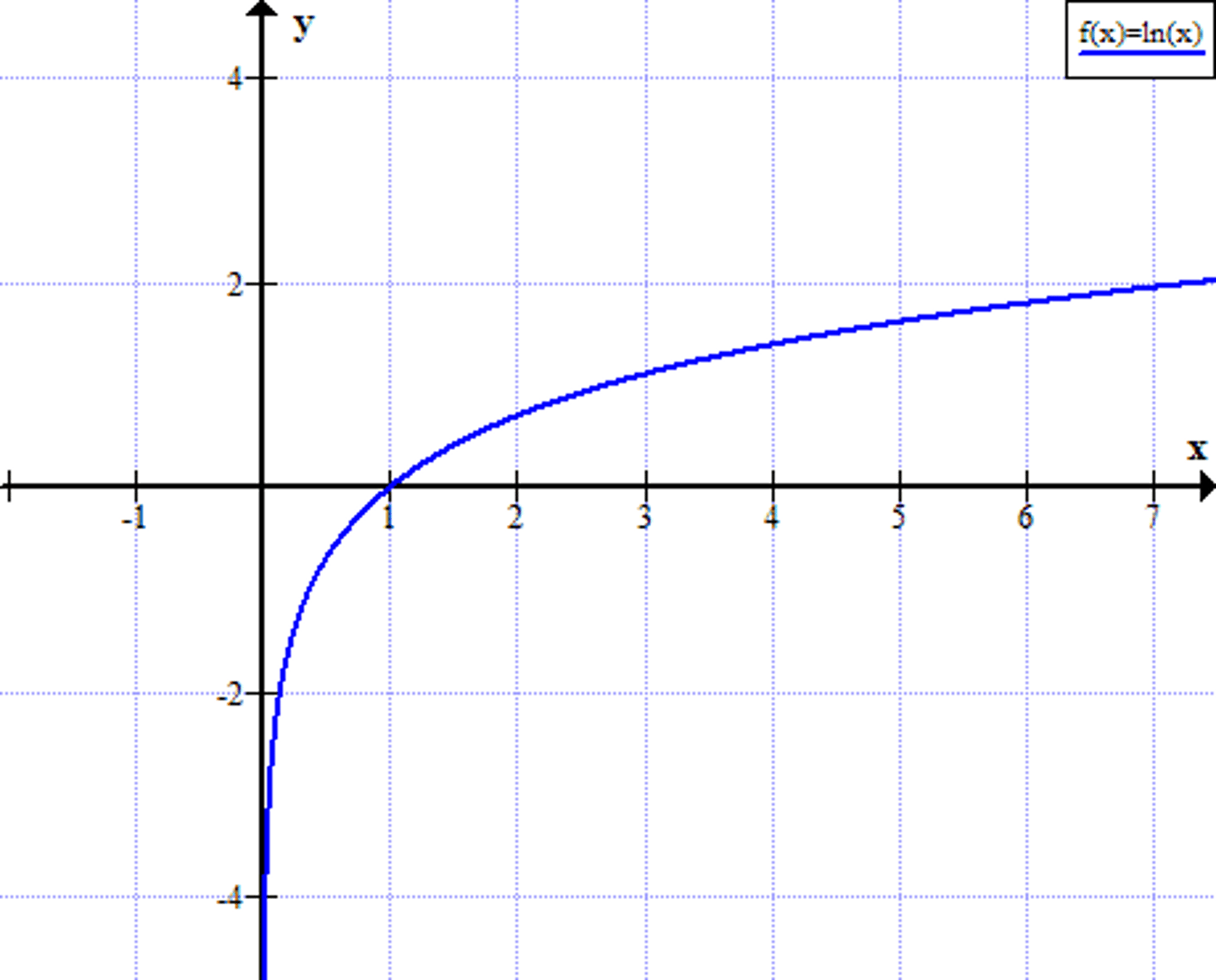
f(x)=ln(x)

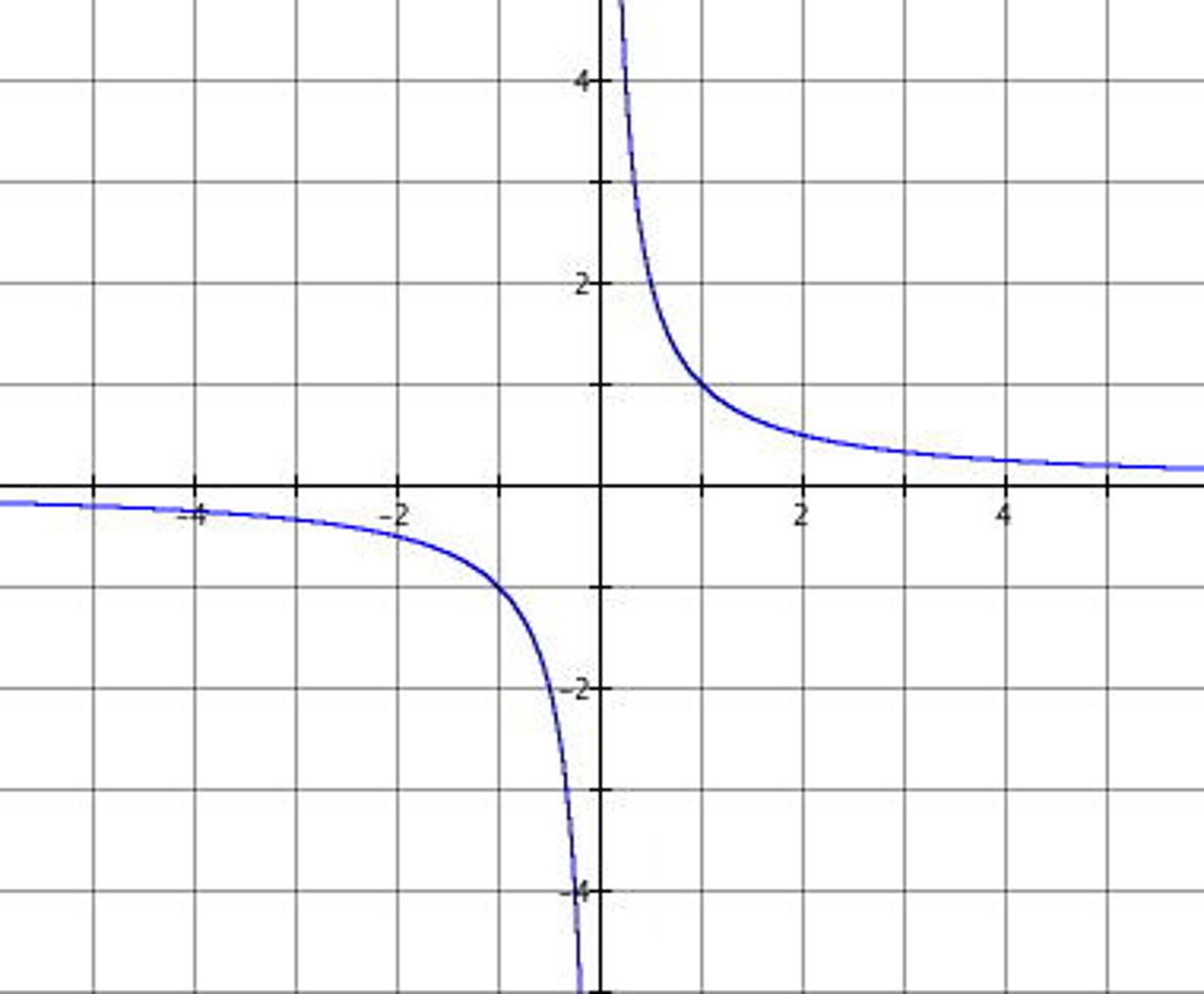
f(x)=1/x

f(x)=1/x²

same as the f(x)=1/x graph except the third quadrant section of the f(x)=1/x graph is reflected across the x-axis and graphed in the second quadrant (volcano graph)

d/dx[c]

0

d/dx[c(x)]

c

d/dx[x^n]

n(x)^(n-1)

d/dx[√x]

1/(2√x)

d/dx[1/x]

-1/x²

d/dx[sin(x)]

cos(x)

d/dx[cos(x)]

-sin(x)

d/dx[tan(x)]

sec²(x)

d/dx[cot(x)]

-csc²(x)

d/dx[sec(x)]

sec(x)tan(x)

d/dx[csc(x)]

-csc(x)cot(x)

d/dx[arcsin(x)]

1/(√1-x²)

d/dx[arccos(x)]

-1/(√1-x²)

d/dx[arctan(x)]

1/(1+x²)

d/dx[arccot(x)]

-1/(1+x²)

d/dx[arcsec(x)]

1/(x√x²-1)

d/dx[arcsc(x)]

-1/(x√x²-1)

d/dx[a^x]

a^(x)ln(a)

d/dx[log↓a(x)]

1/(x)ln(a)

d/dx[e^x]

e^x

d/dx[ln(x)]

1/x

Limit Definition of the Derivative: "h" formula

lim as h approaches 0: f(x+h)-f(x)/h

Limit Definition of the Derivative: "Δx" formula

lim as Δx approaches 0: f(x+Δx) - f(x)/Δx

Limit Definition of the Derivative: "c" formula

lim as h approaches 0: f(c+h)-f(c)/h

Limit Definition of the Derivative: "c with Δx" formula

lim as Δx approaches 0: f(c+Δx)-f(c)/Δx

Limit Definition of the Derivative: "x-c" formula

lim as x approaches c: f(x)-f(c)/x-c

Chain Rule

d/dx[f(g(x))]=f'(g(x))•g'(x)