Stats 2

μ

population mean

x̄

sample mean

σ²

population variance

s²

sample vairance

σ

population standard deviation

s

sample standard deviation

p

population proportion

p̂

sample proportion

confidence interval for population characteristic

range of values that is likely to contain the desired characteristic you’re looking for
Ex: if you have a confidence interval of 95%, then out of all the 100 confidence intervals you have, 5 of the intervals will NOT contain the true mean (the value you’re looking for), but 95 intervals will

steps in constructing confidence intervals

1. write down appropriate formula

2. calculate appropriate critical value

3. substitute values into the formula

4. simplify

5. write solution in interval notation

6. interpret the interval

general form of confidence interval

(pt estimate using a specific statistic) ± (critical value) * (estimated standard deviation of the statistic)

x̄ ± z_α/2 * σ/(√n)

As the ___________ increase, the chi-square curve approaches a __________ __________

degrees of freedom ; normal ; distribution

confidence interval for population variance formula

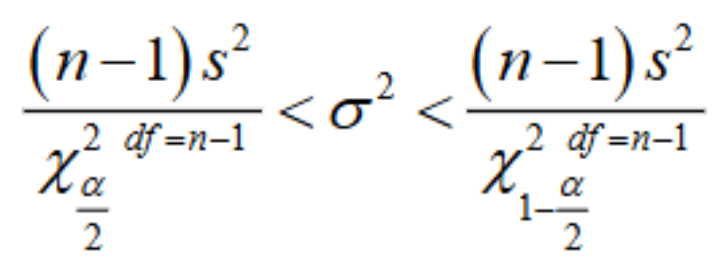
conditions required for a valid confidence interval for σ²

1. random sample is selected

2. the sample selected has a normal distribution (bell-curve)

test of hypotheses/test procedure

use sample data to decide between two competing hypotheses/claims about a population characteristic

null hypothesis

H₀

Claim that is assumed to be true

alternative hypothesis

H_a

Claim that is the opposite of H₀

Form of a null hypothesis

H₀: population characteristic = hypothesized value

H_a: population characteristic > hypothesized value

right-tailed test (one tail)

H_a: population characteristic < hypothesized value

left-tailed test (one tail)

H_a: population characteristic ≠ hypothesized value

two tailed test

Type I error in hypothesis testing

You reject the null hypothesis when it was actually true

Type II error in hypothesis testing

You determine the alt. hypothesis is true when it was actually false

probability of a Type I error is denoted by ___

α

probability of a Type II error is denoted by ____

β

Steps of Test of Hypothesis (using a Rejection Region)

1. define null and alternative hypothesis

2. write down formula of test statistic and indiciate appropriate distribution

3. plug and chug

4. sketch image of distribution

5. calculate and state rejection region

6. write conclusion in context of problem