Addendum CH 5 Derivatives (DONE)

Notation

c:	European call option price
p:	European put option price
S0:	Stock price today
K:	Strike price
T:	Life of option
σ:	Volatility of stock price

 

C:	American call option price
P:	American put option price
ST:	Stock price at option maturity
D:	PV of dividends paid during life of option
r	Risk-free rate for maturity T with cont. comp.

Effect of Variables on Option Pricing (Table 11.1)

 

Variable	c	p	C	P
S0	+	−	+	−
K	−	+	−	+
T	?	?	+	+
σ	+	+	+	+
r	+	−	+	−
D	−	+	−	+

An American option is worth at least as much as the corresponding European option

C ≥ c

P ≥ p

Calls: An Arbitrage Opportunity?

• Suppose that

c = 3	S0 = 20
T = 1	r = 10%
K = 18	D = 0

• Is there an arbitrage opportunity?

Lower Bound for European Call Option Prices; No Dividends (Equation 11.4)

 c ≥ max(S₀ –Ke ^–rT, 0)

Puts: An Arbitrage Opportunity?

• Suppose that

p= 1	S0 = 37
T = 0.5	r =5%
K = 40	D  = 0

• Is there an arbitrage opportunity?

Lower Bound for European Put Prices; No Dividends (Equation 11.5)

 p ≥ max(Ke ^-rT–S₀, 0)

Put-Call Parity: No Dividends
Consider the following 2 portfolios:

• Portfolio A:  European call on a stock + zero-coupon bond that pays K at time T

• Portfolio C:  European put on the stock + the stock

 

		ST > K	ST < K
Portfolio A	Call option	ST − K	0
	Zero-coupon bond	K	K
	Total	ST	K
Portfolio C	Put Option	0	K− ST
	Share	ST	ST
	Total	ST	K

The Put-Call Parity Result (Equation 11.6)

• Both are worth max(S_T , K ) at the maturity of the options

• They must therefore be worth the same today. This means that c + Ke ^-rT = p + S₀      

Arbitrage Opportunities

• Suppose that

c= 3	S0= 31
T = 0.25	r = 10%
K =30	D = 0

• What are the arbitrage  possibilities when      

p = 2.25 ?    

  p = 1 ?

Early Exercise

• Usually there is some chance that an American option will be exercised early

• An exception is an American call on a non-dividend paying stock

• This should never be exercised early

An Extreme Situation

• For an American call option:   

S₀ = 100; T = 0.25; K = 60; D = 0

Should you exercise immediately?

• What should you do if

  • You want to hold the stock for the next 3 months?

  • You do not feel that the stock is worth holding for the next 3 months?

Reasons For Not Exercising a Call Early (No Dividends)

•  No income is sacrificed

•  You delay paying the strike price

•  Holding the call provides insurance against stock price falling below strike price 

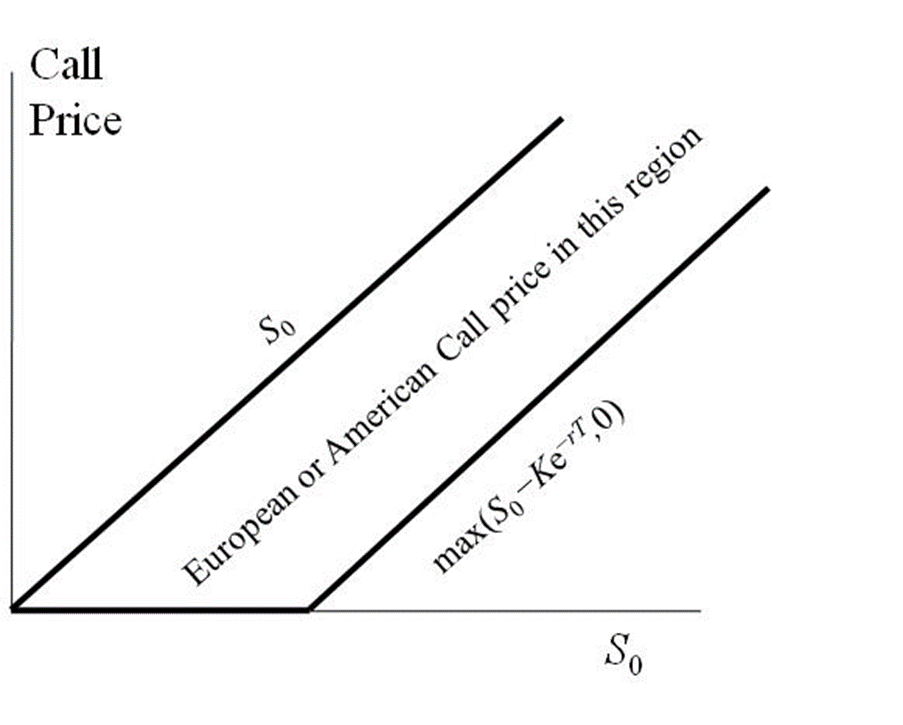
Bounds for European or American Call Options (No Dividends) Figure 11.3

Should Puts Be Exercised
Early ?

Are there any advantages to exercising an American put when      

S₀ = 60; T = 0.25; r=10%

    K = 100; D = 0

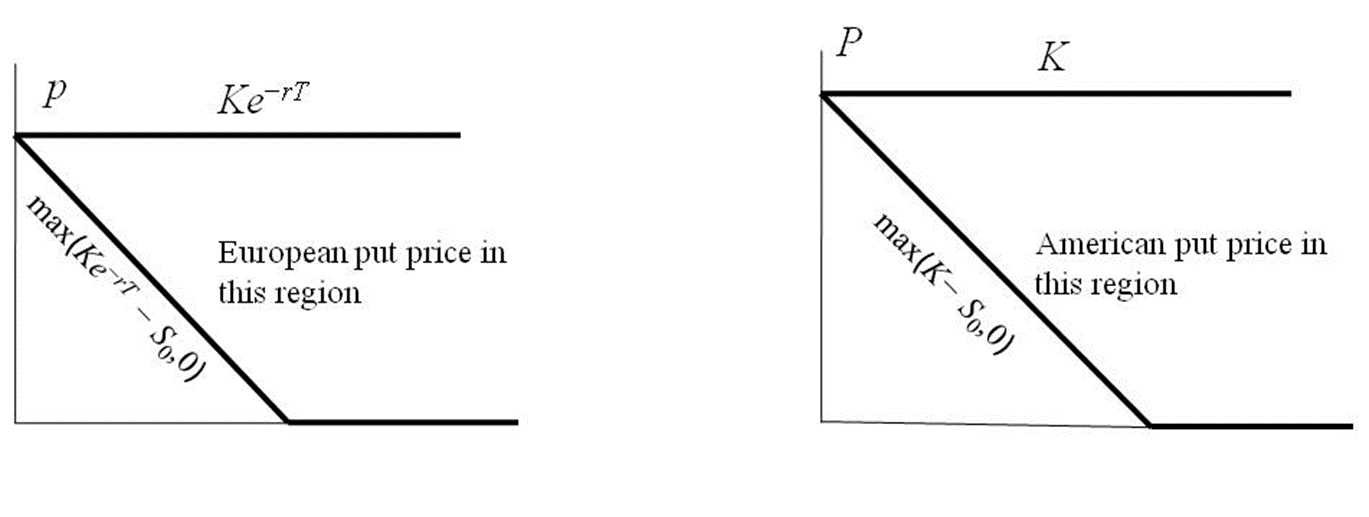
Bounds for European and American Put Options (No Dividends) Figure 11.4

The Impact of Dividends on Lower Bounds to Option Prices
(Equations 11.8 and 11.9)

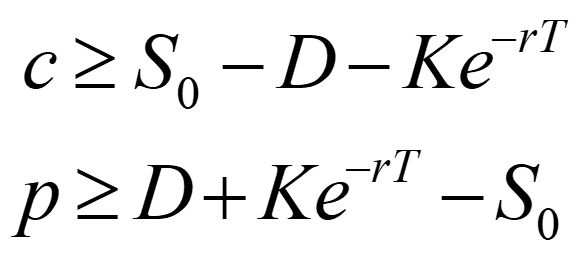
Extensions of Put-Call Parity

• American options; D = 0

S₀ − K < C − P < S₀ − Ke^−rT  

Equation 11.7

• European options; D > 0

c + D + Ke ^−rT = p + S₀    

Equation 11.10

• American options; D > 0

S₀ − D − K < C − P < S₀ − Ke ^−rT

Equation 11.11