Chapter 1: Galilean Relativity

What was Galileo’s thought experiment?

An observer is unaware that they are in a system moving with constant velocity, thus they could reasonably assume they were at rest. If motion is perfectly spot and at constant velocity, Galileo had realised that there would be no experiment capable of distinguishing a system from one that was truly at rest. Due to Newton’s first law, any projectile fired in a frame of constant velocity would behave, relative to that frame, exactly as though that frame was at rest.

What is the Galilean principle of relativity?

Mechanical laws are the same in all inertial frames - it is not possible to conduct a mechanics experiment that would determine that an inertial frame at rest or in uniform motion.

When does the Galilean principle break?

Under acceleration - when the observer sees that all objects seem to be experiencing an accelerating force, that would be some evidence that the frame of reference itself must be accelerating, and so is not at rest.

What is a frame of reference?

A frame of reference is a coordinate system, which has an origin with respect to which you make your measurements for the distance, speed etc.

What is an inertial frame?

The coordinate system is not accelerating - an inertial frame is either at constant velocity or is at rest relative to any other inertial frames.

What is a non-inertial reference frame?

A reference frame that is accelerating. In this frame, an observer will see fictitious forces (e.g. centrifugal), which are evident as the acceleration of an object in the frame without a known force acting on the object.

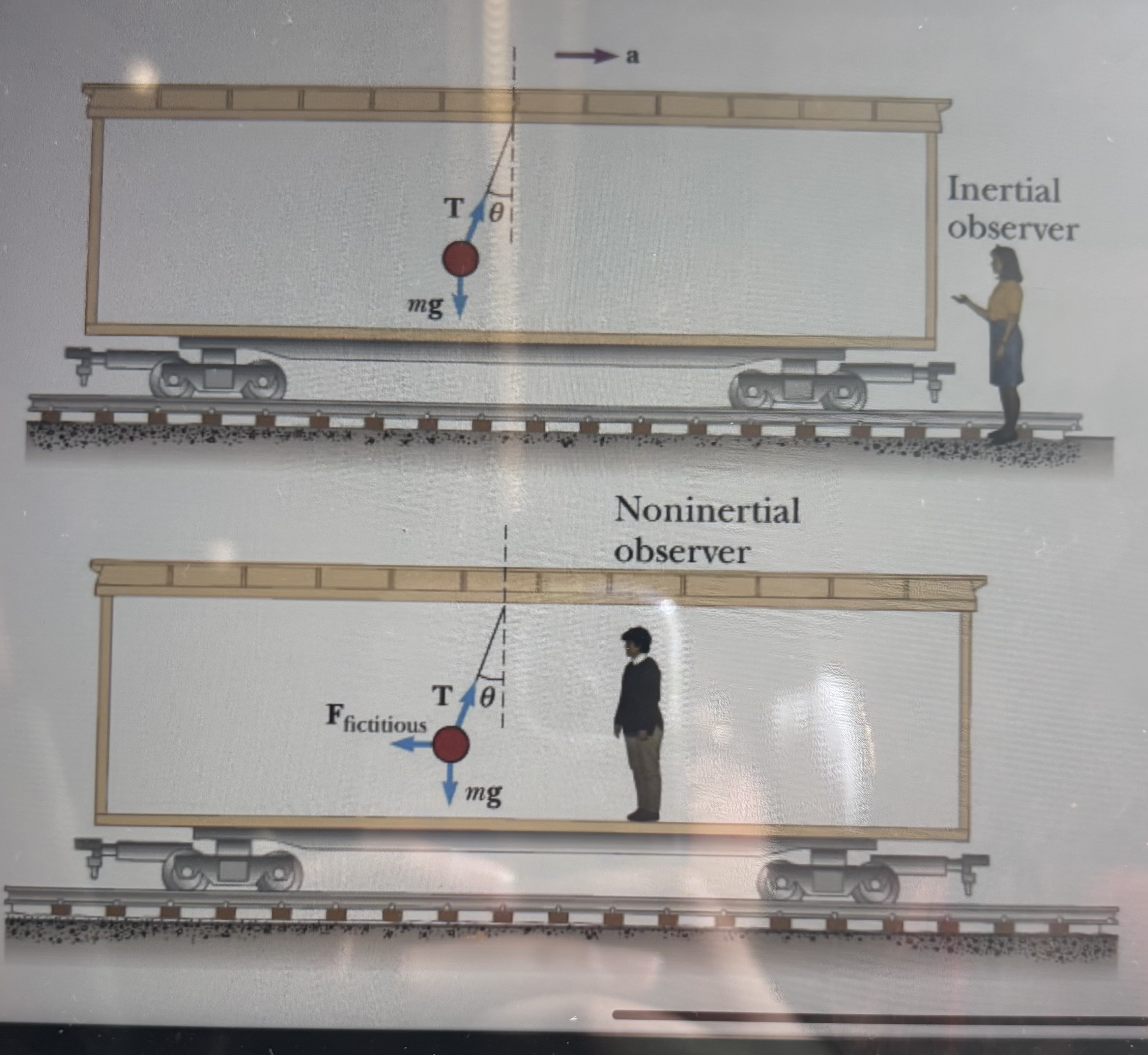
How do the forces affecting the ball on the pendulum differ for an observer outside the train and an observer inside the train?

The outside intertial observer does not require a fictitious force to account for the ball’s acceleration - F=ma=Tsin\theta .

However the inside observer, since they are accelerating with the train, cannot directly measure, or even know, that the train is accelerating. To account for the ball not hanging vertically, they have to include a fictitious force to balance the forces, such that F=Tsin\theta-F_{fictitious}. This is the only way to explain why the ball, relative to this observer, is at rest despite there being tension from the rope. If the non-inertial observer saw the same fictitious force for all their measurements, then they could conclude that there is either some external force acting to pull everything to the left, or that the coordinate system itself is accelerating to the right.

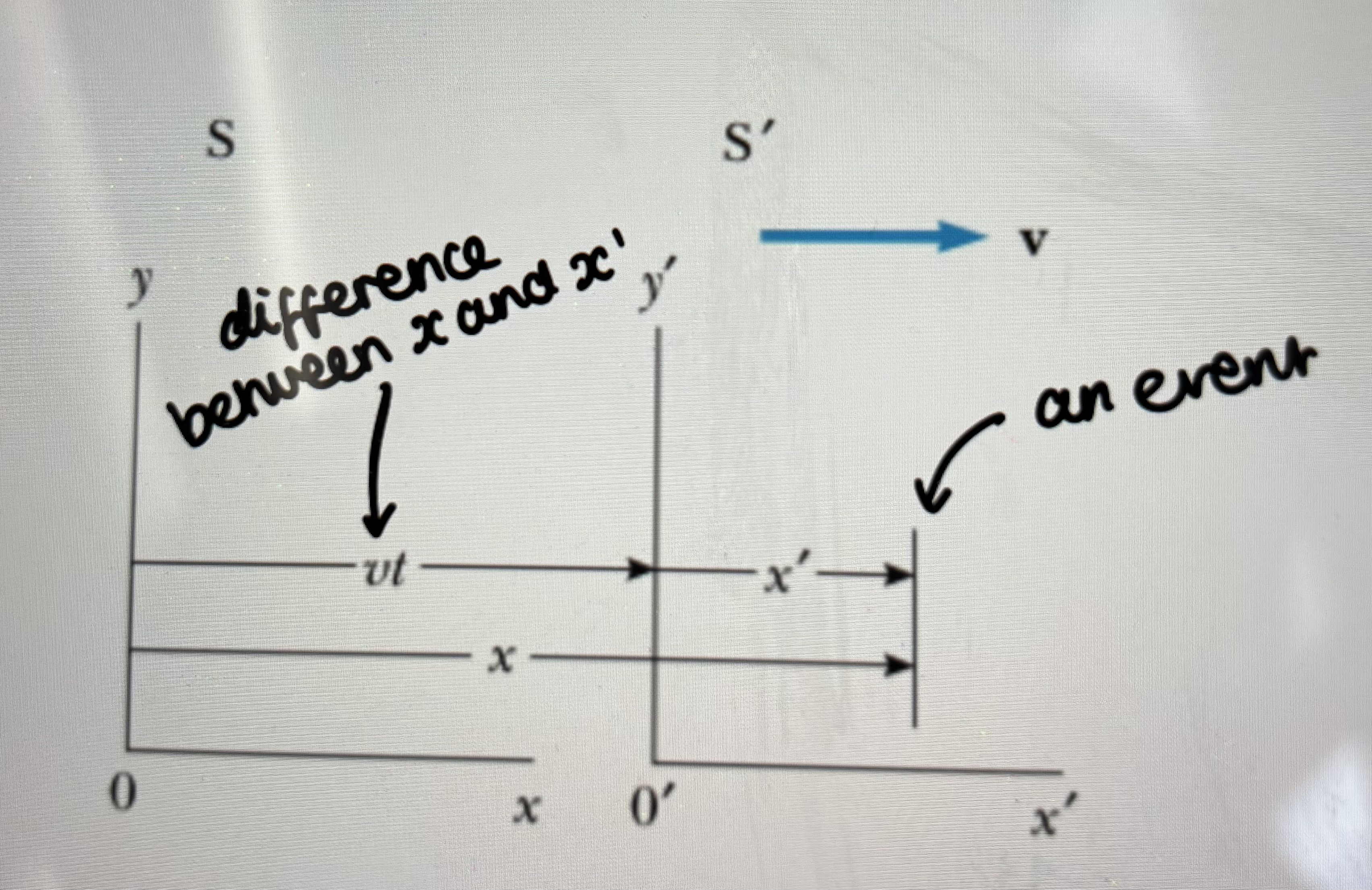
What is the standard configuration of frames?

The axes of both frames are aligned, and initially, at time t=0, both of the frames’ origins are at the same position. This set up is the simplest way to investigate the effect of motion on the different frames of reference.

What is the assumption in Galilean relativity regarding time?

Time follows a universal clock for all inertial frames

What are the Galilean transformations of two frames S and S’?

Since time is universal for all observers, t=t’. However the measurements for the position of the event and the velocity will differ.

x=x’+vt’ or x’=x-vtand y=y’ and z=z’

The observed velocity u of the object is: u=\frac{dx}{dt}=\frac{d(x’+vt)}{dt}=u’+v

Both frames observe the same acceleration as long as v is constant: a=\frac{du}{dt}=\frac{d(u’+v)}{dt}=\frac{du’}{dt}=a’

What were Newton’s views of space and time?

1. Absolute space: A fixed, infinite, and immovable framework that exists independently of objects, serving as the true reference for all motion and rest, distinct from relative space defined by the positions of objects

2. Universal time: A single, absolute, and unchanging flow of time that progresses uniformly and independently of any external influences or observations, distinct from relative, perceived time measured by clocks or celestial movements.

What were the criticisms of of Newtonian space and time?

His own theory showed that there could be no way to measure an objects speed relative to this absolute background of space I.e the Galilean principle is still in effect - he still says that it is impossible to do measurements relative to absolute space. However, since Newton’s other work was groundbreaking and accurate, his views on space and time were also widely accepted.

In what way was Newtonian space and time correct?

Universal time is a concept required for Newtonian mechanics. Newtonian mechanics doesn’t require absolute space - this was an extra assumption he was making in his arguments.

What is the Doppler shift?

A moving sound source will have its frequency shifted because as its moving and producing the up and down motion that produces the sound, their will be slightly more compressed in the direction of travel, which compresses the wavelengths of sound. So you will hear a higher pitch that what you’re actually emitting, and as the sound moves away from you again, the wavelengths are stretched and you’ll hear a lower pitch that what was actually being emitted.

Why was the Doppler effect ineffective in measuring absolute motion?

The Doppler effect is not observed inside a sealed container as the air and the object are moving at the same velocity. Since sound requires a medium to travel through, it would not be possible to know if the change in sound frequency is due to the frame moving, or if it is due to the medium itself having a velocity relative to the frame - both situations produce the same Doppler effect.

How did Maxwell prove that E-fields and B-fields propogate as waves through space?

Maxwell equations: \frac{\delta²E}{\delta x²}= \epsilon_0 \mu_0 \frac{\delta²E}{\delta t²} and \frac{\delta²B}{\delta x²}= \epsilon_0 \mu_0 \frac{\delta²B}{\delta t²}

General linear wave equation: \frac{\delta²y}{\delta x²}= \frac{1}{v²} \frac{\delta²y}{\delta t²}

\epsilon _0 is vaccum permittivity

\mu_0 is vaccum permittivity

y is wave displacement

v is the speed of the propogating wave

By comparing the Maxwell equations to the already well known general linear equation, Maxwell could prove that their forms were identical.

How did Maxwell prove that light was an electromagnetic wave?

Maxwell equations: \frac{\delta²E}{\delta x²}= \epsilon_0 \mu_0 \frac{\delta²E}{\delta t²} and \frac{\delta²B}{\delta x²}= \epsilon_0 \mu_0 \frac{\delta²B}{\delta t²}

Maxwell had shown that the waves would have a velocity given by (\epsilon_0 \mu_0)^{-1/2} and with consistent units for the constants,, this speed in a vaccum would be 3.00×10^8 m/s .

This result showed that the calculated speed was identitical to the experimentally measured speed of light, which proved that light was an EM wave.

How was Newton, who advocated for a particle theory of light (corpuscular light) proven wrong by Maxwell?

Maxwell showed that light was an EM wave, and within a few years, diffraction experiments were conducted confirming Maxwell’s work.

Maxwell had shown that the waves would have a velocity given by (\epsilon_0 \mu_0)^{-1/2} and with consistent units for the constants,, this speed in a vaccum would be 3.00×10^8 m/s .

How did this result show that light was a universal constant?

The speed is made of two universal constants, thus making the speed of the EM wave in a vaccum itself a universal constant - however this result was not considered seriously.

What is the luminous aether?

An undetected medium that scientists hypothesised light travelled in. All previously known waves were mechanical waves, and as such, required a medium to propograte through.

What was the initial assumption about the aether and its relationship to the speed of light?

Since light propogates through all of space, the aether too, must fill all the space. Since the speed of light was made of constants, the aether was supposed to be a medium at rest relative to the absolute background of space that Newton had required in his theories.

What did the Galilean transformation predict about the observed speed of light when an observer is moving relative to the aether?

The simple Galilean transformation gives the observed speed of light c_{obs}=c+v \rightarrow if an observer was moving relative to the aether, with some speed v, it should have been possible to measure the speed of light changing by \pm v

Why couldn’t the speed of motion through the aether be shown through observing how the Earth’s motion affected the speed of light?

Since the speed of light was so much faster that the speed of the Earth’s orbit around the sun, the sensitivity of the experiment was well beyond the capacity of the time - interference patterns reply on the wavelength of light being very small. Tiny differences in the path travelled by light could induce interference fringes.

What is the theory behind the Michelson-Morley experiment?

The frequency of light is sensitive to constructive and destructive interference caused by path differences. A beam of monochromatic light is split into two perpendicular beams - one path would travel in the direction of the Earth’s motion through the aether, the other would travel perpendicular. Both beams were reflected back with a mirror after travelling equal distances.

If the experiment was at rest relative to the aether, the paths would be identical, and so there would be constructive interference when they meet. However, since the Earth is moving, the one parallel to the Earth’s motion will have to travel further because the mirror moves relative to the aether, effectively increasing the length of the journey. Similiarly, on the return journey, the start point moves towards the light in the aether, which shortens the path, but not enough to completely cancel the increase.

How were defects in the experimental setup for the Michelson-Morley experiment accounted for?

They were accounted for systematically by mounting the entire experiment on a pool of mercury and rotating it.

What does the diagram for the Michelson-Morley experiment look like?

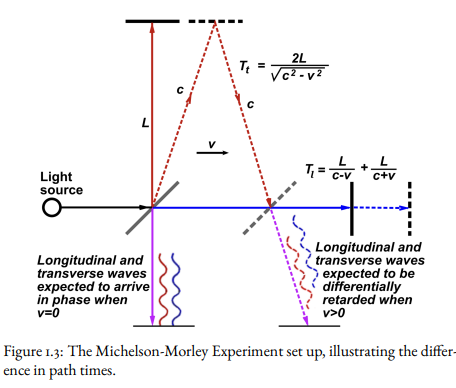
Why was the Michelson-Morley experiment ideal for measuring any changes in the speed of light?

Interference patterns are highly sensitive to even slight variations in path difference, which made this process ideal for measuring the tiny fractional change in the measured speed of light.

What were the expected results of the Michelson-Morley experiment?

The expected time difference is roughly \Delta t = \frac{2L}{c}[(1-\frac{v²}{c²})^{-1}-(1-\frac{v²}{c²})^{-1/2}]=\frac{Lv²}{c³} where L is the path length of the speed of light, c is the speed of light and v is the relative velocity of the Earth through the aether. We have an expected shift in the pattern of n=0.44 .

What was the final result of the Michelson-Morley experiment?

No shift in interference pattern was detected, regardless of the orientation of the apparatus. The motion of the Earth through the aether could not be detected. The speed of light appeared constant in al directions.

This nul result disproved the existence f the aether and suggested that the sped of ight is invariant, a cornerstone for the development of special relativity.

Which two postulates did Einstein use to explain the Michelson-Morley result?

• The laws of physics must be the same in all inertial reference frames

• The speed of light in a vacuum is the same in all inertial frames - implicitly claiming that light does not require a medium

Together, these postulates Form the foundation of special relativity, leading to a new understanding of space, time and motion.

What did Einstein’s first postulate (the laws of physics must be the same in all inertial frames) explain about the Michelson-Morley experiment?

Einstein took the original Galilean principle more seriously, and rather than trying to see if light can be used to disprove it, instead included electromagnetism and optics with mechanics, and claimed that they were subject to the same limitations, that is, they could not distinguish between an observer at rest and one in uniform motion.

Einstein concluded that there was no aether, and so EM waves were the first waves discovered that didn’t require a medium.

What did Einstein’s second postulate (the speed of light in a vacuum is the same in all inertial reference frames) explain about the Michelson-Morley experiment?

Einstein concluded that the only way for the speed of light to be constant in all inertial reference frames was if time and space distort in just the right way to make that true. Einstein then set about mathematically describing what the implications of time dilation and length contraction would mean for physics and mechanics.

How did Lorentz explain the result of the Michelson-Morley experiment?

He claimed that objects in motion, such as the Earth, may perceive distances and time in a distorted way. Objects in motion experience time dilation and length contraction. However, he did not take his own result seriously and thought these effects were just an artefact of motion. He also still believed there was an aether.