Math 305: Ordinary Differential Equations

What is a differential equation

An equation involving a derivative. Its a relation between a function and its derivatives (September 3, 1.1) (Exam 1 Material)

What does the order of a differential equation refer too

The highest derivative in the entire equation (September 3, 1.1) (Exam 1 Material)

What is a general solution

Like a family of solutions. Does not refer to one single solution (September 3, 1.1) (Exam 1 Material)

If you have a constant equal to x, is y(x) truly a solution to the equation

No. Because y(x) is not a solution on a given interval, only at 1 point (September 3, 1.1) (Exam 1 Material)

How do you solve a differential equation in the form dy/dx = f(x)

Integrate f(x)dx and add a constant C. (September 5, 1.2) (Exam 1 Material)

2nd order differential equations require how many initial conditions to arrive at a particular solution?

2 (September 5, 1.2) (Exam 1 Material)

Position, velocity, and acceleration share what relationship

a(t) = v’(t) = x’’(t) (September 5 1.2) (Exam 1 Material)

Summarize the Existence and Uniqueness Theorem.

1. Continuity of f(x,y) on a rectangle R guarantees the existence of the solution.

2. Continuity of the partial derivative of f(x,y) with respect to y on Rectangle R guarantees the uniqueness (only one solution) of the solution (September 8, 1.4)

(Exam 1 Material)

Separation of variables can be used when

y’ = f(x)g(y) (September 8, 1.4) (Exam 1 Material)

Implicit General Solution

A solution to a differential equation where integration was completed but y was not solved for. (September 8, 1.4) (Exam 1 Material)

Explicit General Solution

A solution to a differential equation in the form y = f(x). y = something (September 8, 1.4) (Exam 1 Material)

What is the general form of a first order linear equation

(September 10, 1.5) (Exam 1 Material)

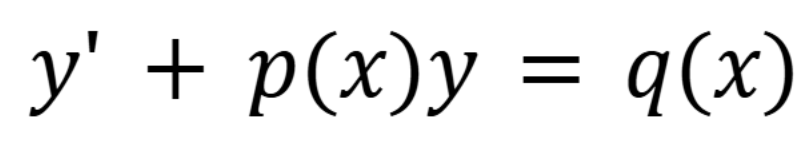
Integrating Factor Formula

(September 10, 1.5) (Exam 1 Material)

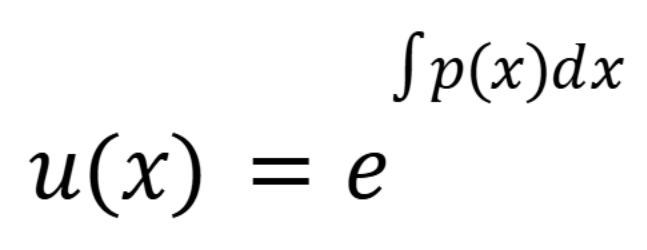
Other formula related to integrating factoring

(September 10, 1.5) (Exam 1 Material)

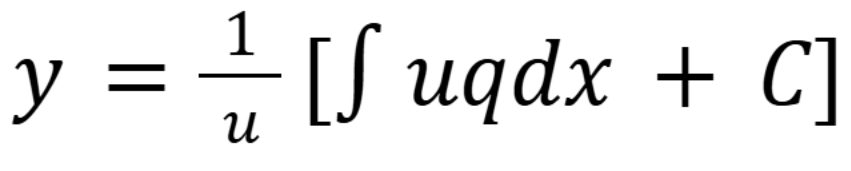
What is the general form of a homogenous 1st order differential equation.

(September 12, 1.6) (Exam 1 Material)

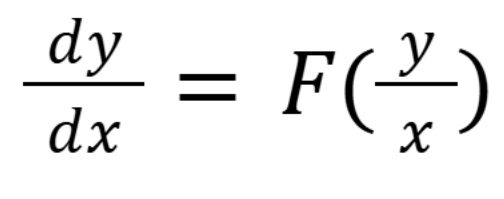
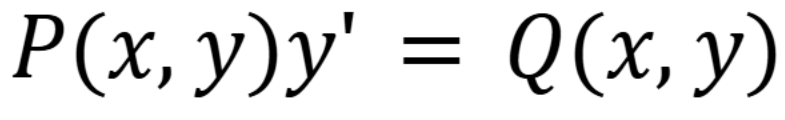
If this equation is a homogenous 1st order differential equation, what must be true.

The degree of each term in P and Q are the same. (September 12, 1.6) (Exam 1 Material)

What substitution must you make to solve a homogenous 1st order differential equation

Note, V is a function of x. (September 12, 1.6) (Exam 1 Material)

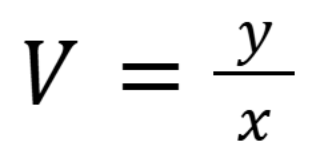
If you simplify a homogenous 1st order differential equation correctly, what other type of equation should result

A separable differential equation (September 12, 1.6) (Exam 1 Material)

What is the general form for Bernoulis’s Equation

n does not have to be an integer (September 12, 1.6) (Exam 1 Material)

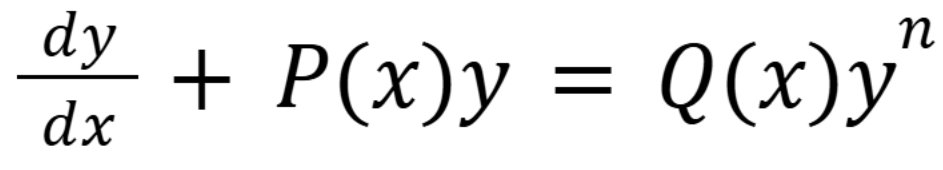
What substitution must you make to solve a Bernoulis’s Equation problem

When solving these problems, remember to only have y and x in your final answer. (September 12, 1.6) (Exam 1 Material)

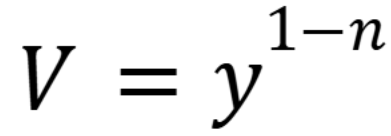
If you simplify a Bernoulis’s equation correctly, what other type of equation should result

1st order linear differential equation (September 12, 1.6) (Exam 1 Material)

What is the general form of exact equations

(September 15, 1.6) (Exam 1 Material)

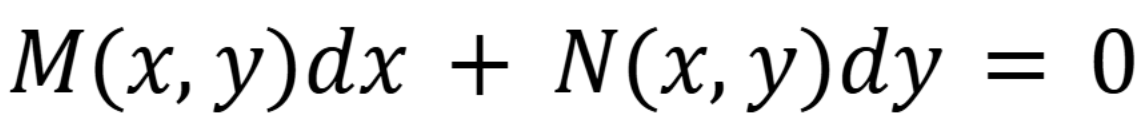
What must be true for an equation to be exact.

(September 15, 1.6) (Exam 1 Material)

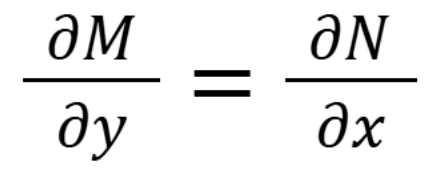
When you take the partial derivative of M, in an exact equation. what do you take it with respect to

Y (September 15, 1.6) (Exam 1 Material)

When you take the partial derivative of N, in an exact equation. what do you take it with respect to

X (September 15, 1.6) (Exam 1 Material)

If y is absent in a reducible 2nd order differential equation, then what substitution must you make.

p = y^’ and p^’= y^’’ (September 17, 1.6) (Exam 1 Material)

If x is absent in a reducible 2nd order differential equation, then what substitution must you make.

(September 17, 1.6) (Exam 1 Material)

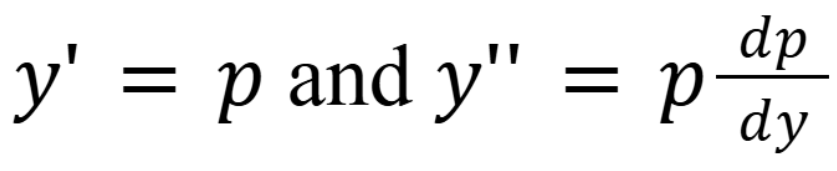
What’s the general form of a logistic equation 

(September 22, 2.2) (Exam 2 Material)

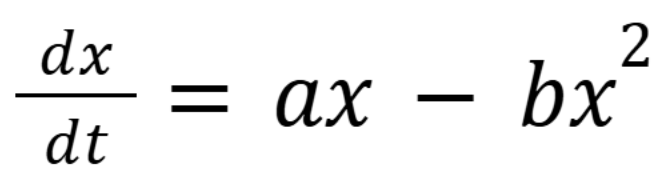
When solving equilibrium solutions and stability problems, what must you show. 

1. The critical points

2. Intervals for which dx/dt is positive and negative

3. Phase diagrams, indicating stability and positives and negatives

4. Solution curves with x usually as the vertical axis and t usually as the horizontal axis

(September 22, 2.2) (Exam 2 Material)

When drawing phase diagrams, when is a critical point stable

Goes from positive to negative. Goes from » to «. (September 22, 2.2) (Exam 2 Material)

When drawing phase diagrams, when is a critical point Unstable

Goes from negative to positive. Goes from « to » (September 22, 2.2) (Exam 2 Material)

When drawing phase diagrams, when is a critical point semi-stable

Does not change signs. Stays positive or stays negative. (September 22, 2.2) (Exam 2 Material)

General form of a 2nd order linear differential equation

(September 24. 3.1) (Exam 2 Material)

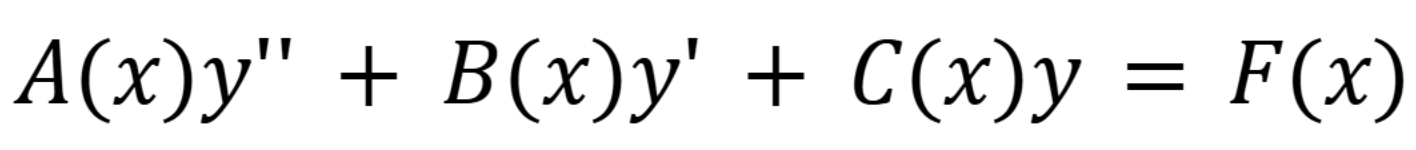
How do you determine if two functions are linearly independent solutions

If there ratios are NOT a constant, then they are linearly independent. (September 24. 3.1) (Exam 2 Material)

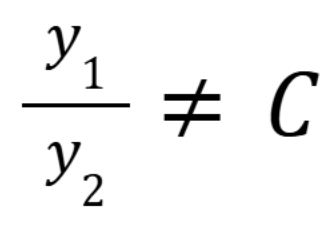
General form for finding two constants of a 2nd order linear differential equation

(September 24. 3.1) (Exam 2 Material)

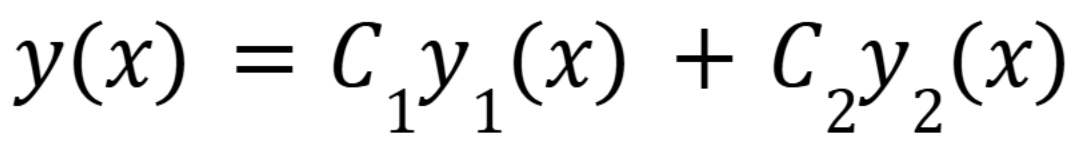
What’s the general form of a 2nd order linear differential equation with constant coefficients.

(September 26. 3.1) (Exam 2 Material)

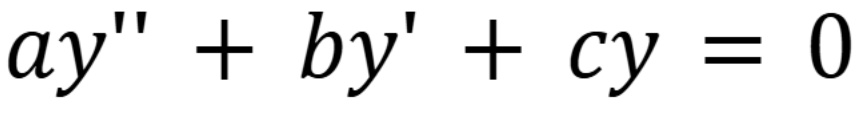
How do you solve 2nd order linear differential equations with constant coefficients when there’s two distinct real solutions

Use y = e^rx. Use y(x) = C₁y₁ + C₂y₂ and set ar²+br+c=0. Find r₁ and r₂ (September 26. 3.1) (Exam 2 Material)

How do you solve 2nd order linear differential equations with constant coefficients when there’s 1 real solution

Use y = (C₁+C₂x)e^rx (September 26. 3.1) (Exam 2 Material)

What substitution must you make when solving Euler’s equations

V = lnx. And note y = y(v). (September 26. 3.1) (Exam 2 Material)

For an n-th order homogenous differential equation with constant coefficients, what is the general solution

(October 1. 3.3) (Exam 2 Material)

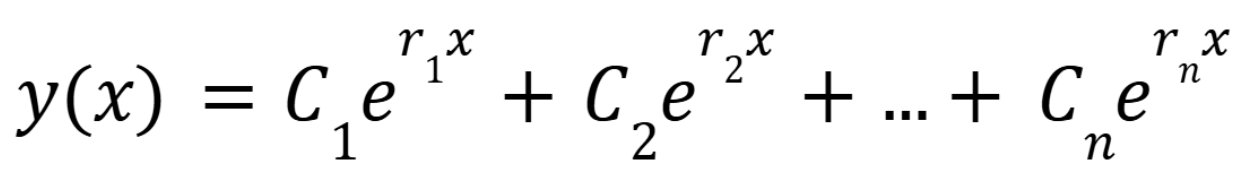
If a real root r is repeated m times (the multiplicity is m) , in an n-th order homogenous differential equation with constant coefficients, how many terms must be in that factor

m terms (October 1. 3.3) (Exam 2 Material)

What is the general solution of a n-th order homogenous differential equation with constant coefficients with imaginary roots.

(October 3. 3.3) (Exam 2 Material)

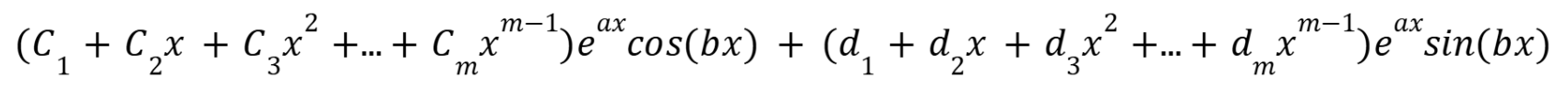
What is the form of the differential equation for a mass-spring system.

(October 6. 3.4) (Exam 2 Material)

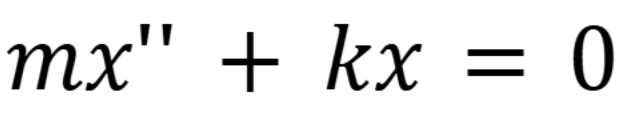
What equation relates the period T and omega.

(October 6. 3.4) (Exam 2 Material)

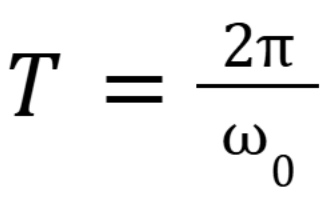
What equation relates frequency and omega.

(October 6. 3.4) (Exam 2 Material)

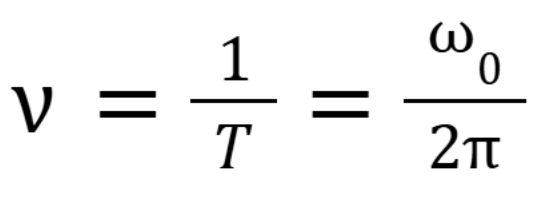
What equation relates the time lag, delta, and alpha and omega.

(October 6. 3.4) (Exam 2 Material)

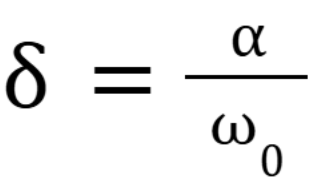
What is the equation for position as a function of time for a mass-spring system

(October 6. 3.4) (Exam 2 Material) (There should be a C in front of cosine. NEED TO FIX)

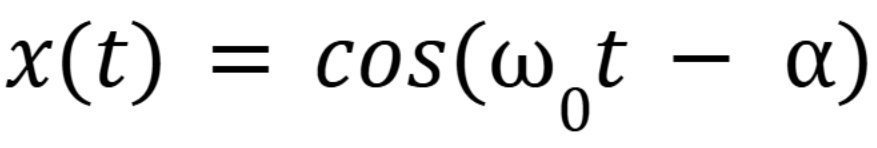
When is a mass-spring-dashpot system underdamped

When you get imaginary roots from the characteristic equation (October 10. 3.4) (Exam 3 Material)

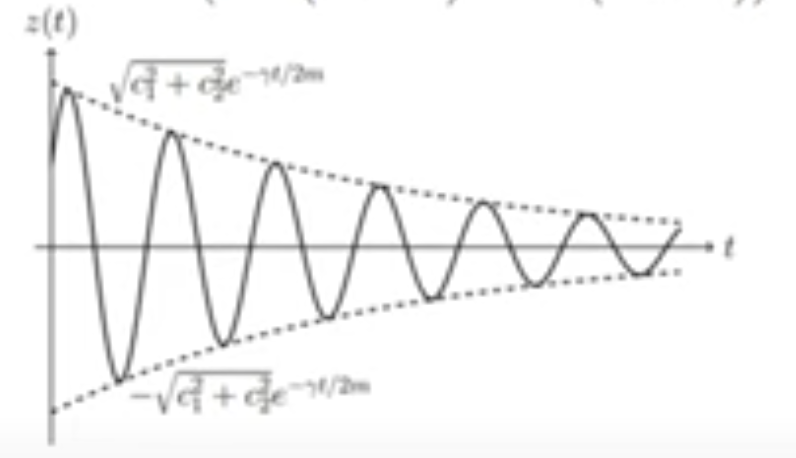
When is a mass-spring-dashpot system overdamped

When you get two distinct real roots from the characteristic equation (October 10. 3.4) (Exam 3 Material)

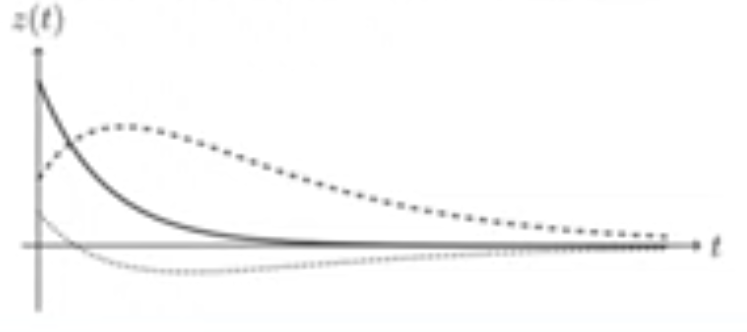
When is a mass-spring-dashpot system critically damped

When there is one single real root (October 10. 3.4) (Exam 3 Material)

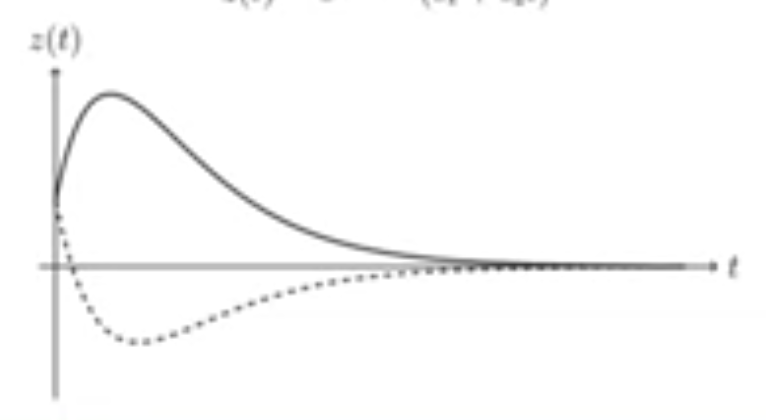
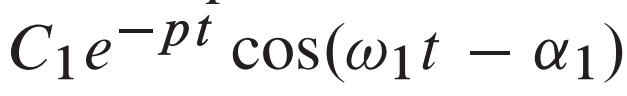
If we have a mass-spring-dashpot system, that’s underdamped and the equation x(t) is in the form shown in the image, what is the value of p

c/2m. c is the damping constant (October 10. 3.4) (Exam 3 Material)

What is the formula you should use for the method of variation of parameters

(October 13. 3.5) (Exam 3 Material)

How do you get rid of duplications when using the method of undetermined coefficients 

Multiply the duplication part by x^s where s is the smallest integer greater than 0 that will get rid of duplication. (October 13. 3.5) (Exam 3 Material)

What is the period for a mass spring dashpot system

(October 17. 3.6) (Exam 3 Material)

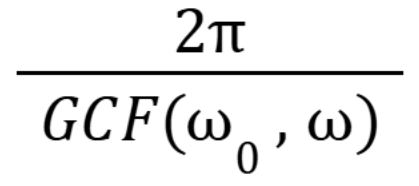
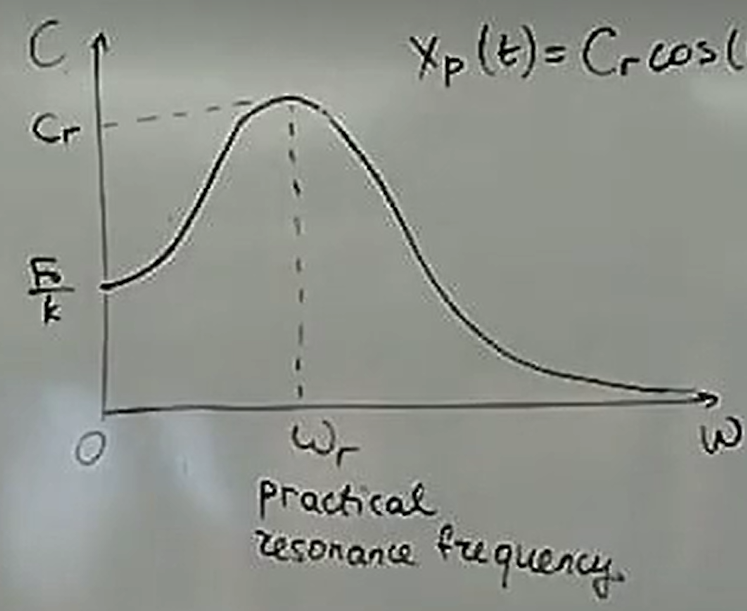
How do I know if practical resonance is possible

If there is a maximum in the C(omega) graph, then yes there’s practical resonance (October 20. 3.6) (Exam 3 Material)

What is the practical resonance frequency formula

(October 20. 3.6) (Exam 3 Material)

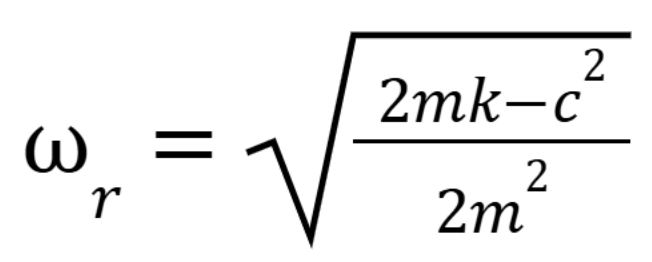
What is the vertical intercept of a C(omega) graph

F₀/k (October 20. 3.6) (Exam 3 Material)

If practical resonance is present, what should the graph look like.

(October 20. 3.6) (Exam 3 Material)

What is the general representation for the Fourier series

(October 22. 9.1) (Exam 3 Material)

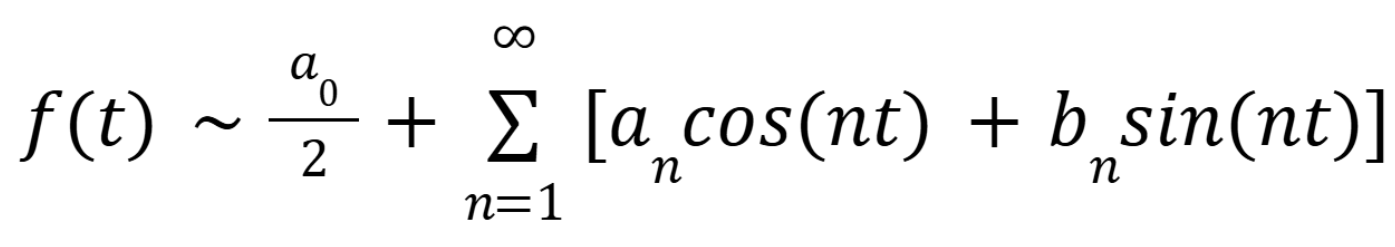
How do you find a₀ for the Fourier series

(October 22. 9.1) (Exam 3 Material)

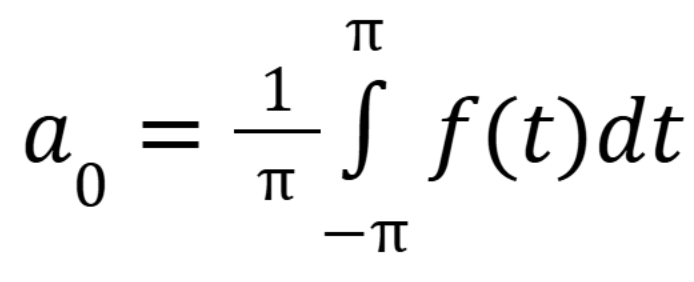
How do you find a_n for the Fourier series

(October 22. 9.1) (Exam 3 Material)

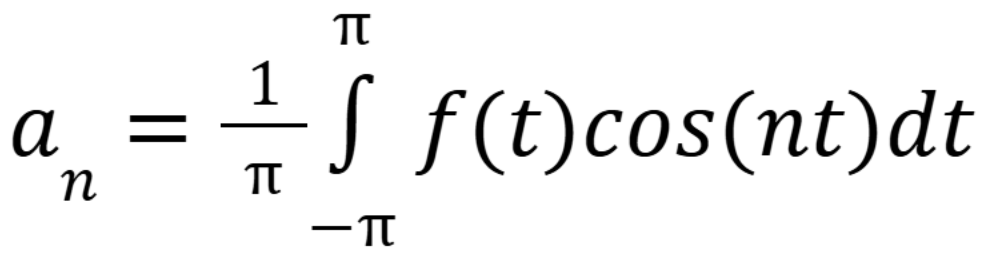
How do you find b_n for the Fourier series

(October 22. 9.1) (Exam 3 Material)

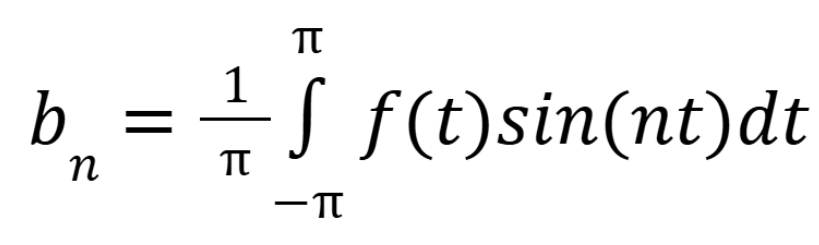
What’s another way to express cos(n pi)

as (-1)ⁿ this is for odd values of n. (October 22. 9.1) (Exam 3 Material).

Consider a function f(t) with a period of 2L. The Fourier series for this function is what

In this case, the coefficient of the integral would be 1/L. (October 22. 9.2) (Exam 3 Material).

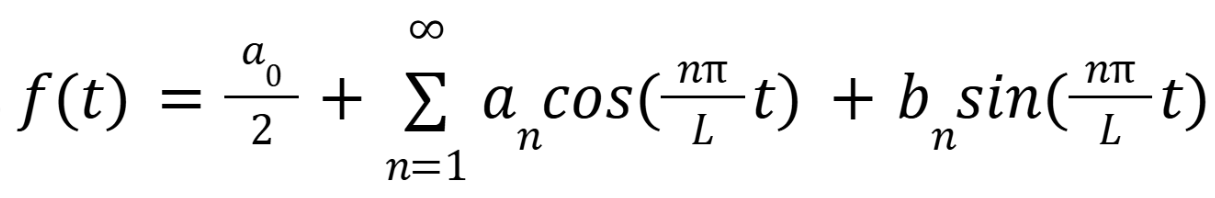
If given boundary conditions, x(0)=0=x(L), what series must we use

We must use the sine series for f(t) (October 24. 9.3) (Exam 3 Material).

What does it mean for a function be odd

f(t) = -f(-t) (October 24. 9.3) (Exam 3 Material).

What does it mean for a function be even

f(t) = f(-t) (October 24. 9.3) (Exam 3 Material).

What is the definition of the Laplace Transform

(November 5. 7.1) (Exam 4 Material).

What’s the sum and constant rule for laplace transforms

(November 5. 7.2) (Exam 4 Material).

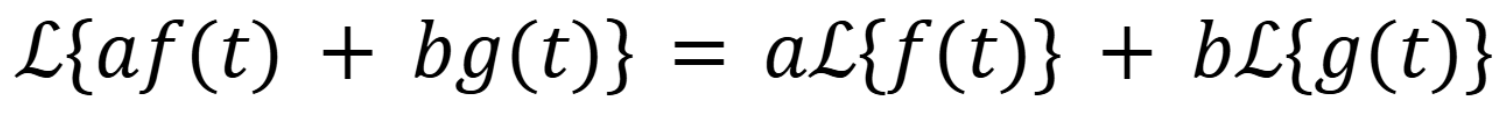
What is the laplace transform of e^at where a is a real number

(November 5. 7.2) (Exam 4 Material).

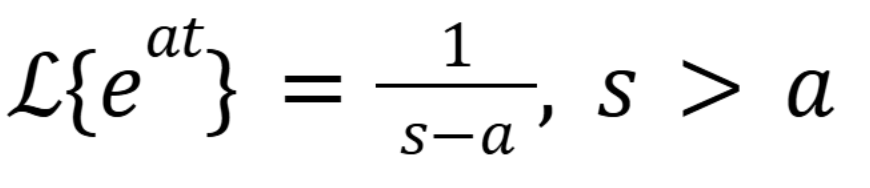
What is the laplace transform of sin(kt) where k is a real number

(November 5. 7.2) (Exam 4 Material).

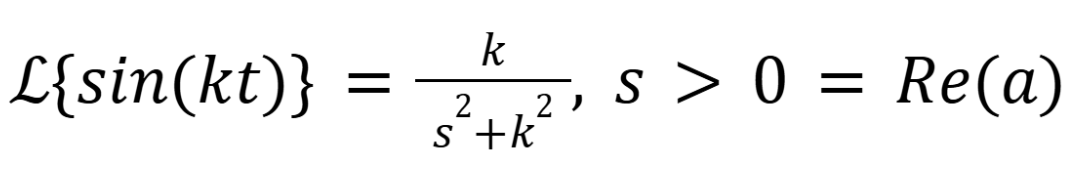
What is the laplace transform of cos(kt) where k is a real number

(November 5. 7.2) (Exam 4 Material).

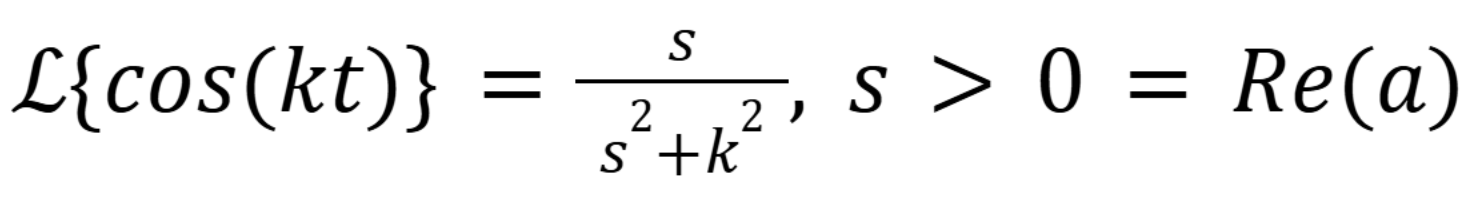
What is the laplace transform of tⁿ where n is a positive integer

(November 5. 7.2) (Exam 4 Material).

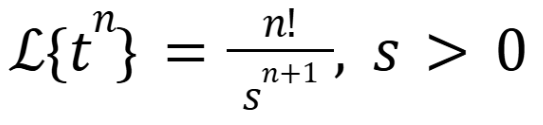
What is the laplace transform of t^a where a>-1

(November 5. 7.2) (Exam 4 Material).

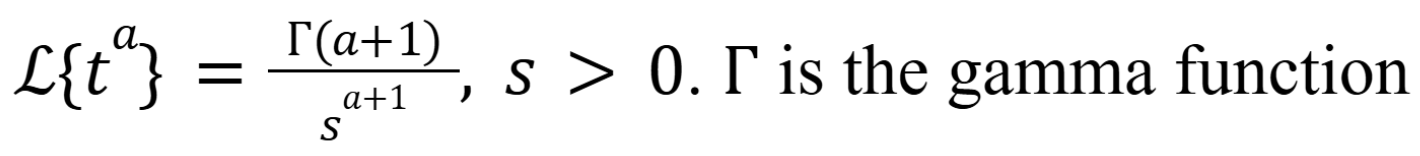
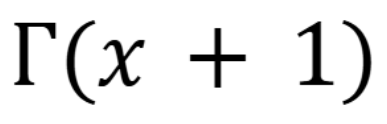
In the image shown, what is it equivalent too

(November 5. 7.2) (Exam 4 Material).

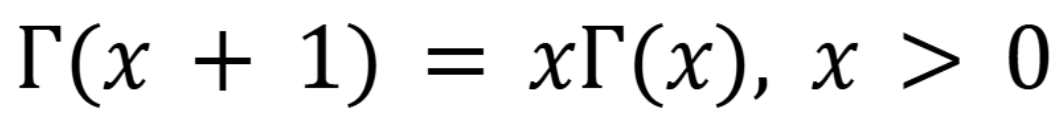
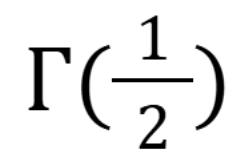
In the image shown, what is it equivalent too

(November 5. 7.2) (Exam 4 Material).

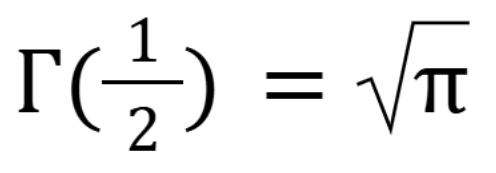
What is the laplace transform of sinh(kt) where k is a real number

(November 7. 7.1) (Exam 4 Material).

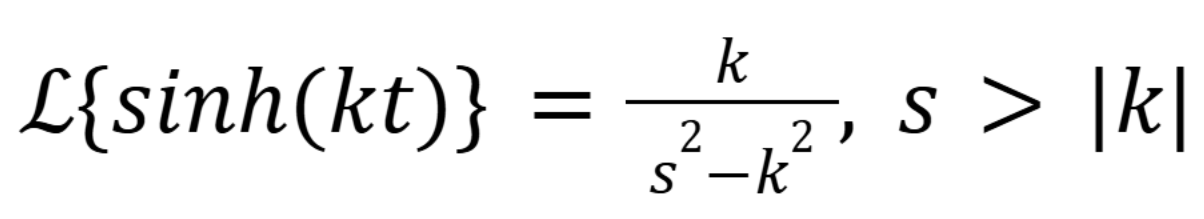
What is the laplace transform of cosh(kt) where k is a real number

(November 7. 7.1) (Exam 4 Material).

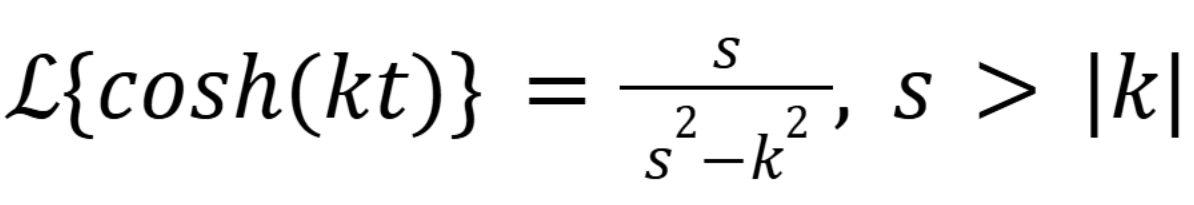
What is the laplace transform of x’(t)

(November 10. 7.2) (Exam 4 Material).

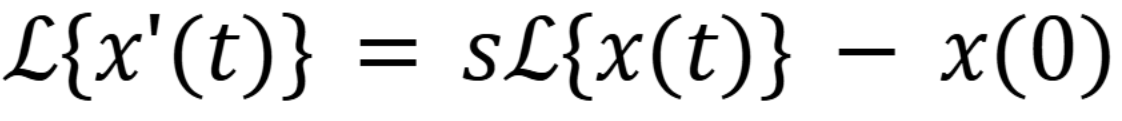
What is the laplace transform of x’’(t)

(November 10. 7.2) (Exam 4 Material).

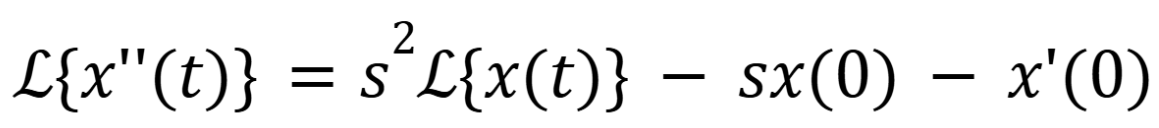
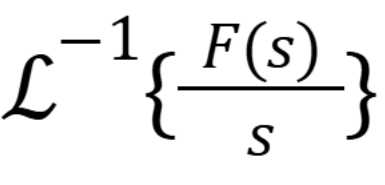
What is the equivalent form of the image shown

(November 10. 7.2) (Exam 4 Material).

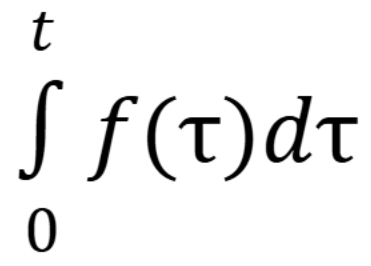
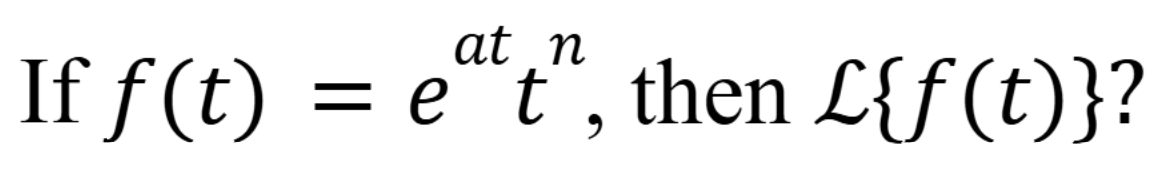
(November 12. 7.3) (Exam 4 Material).

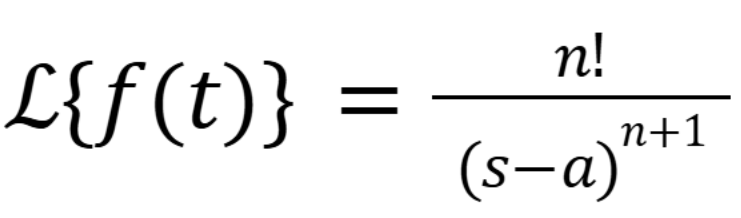
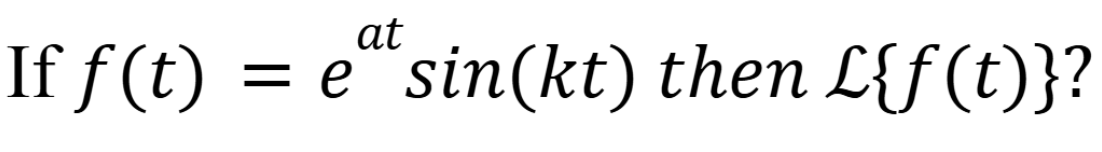
(November 12. 7.3) (Exam 4 Material).

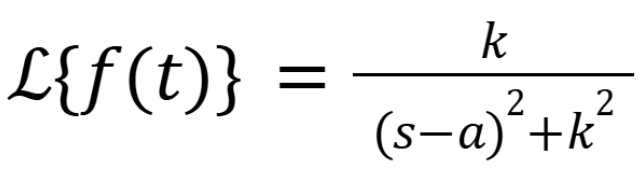
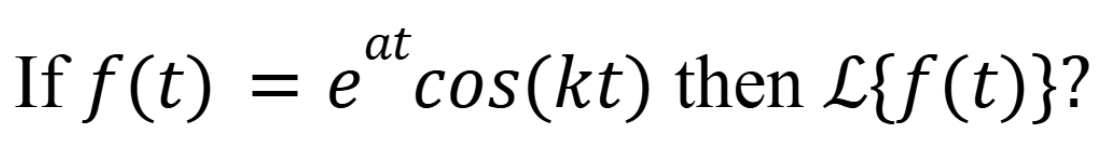
(November 12. 7.3) (Exam 4 Material).

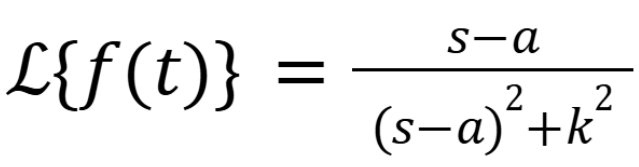
What is the convolution of 2 functions

(November 14. 7.4) (Exam 4 Material).

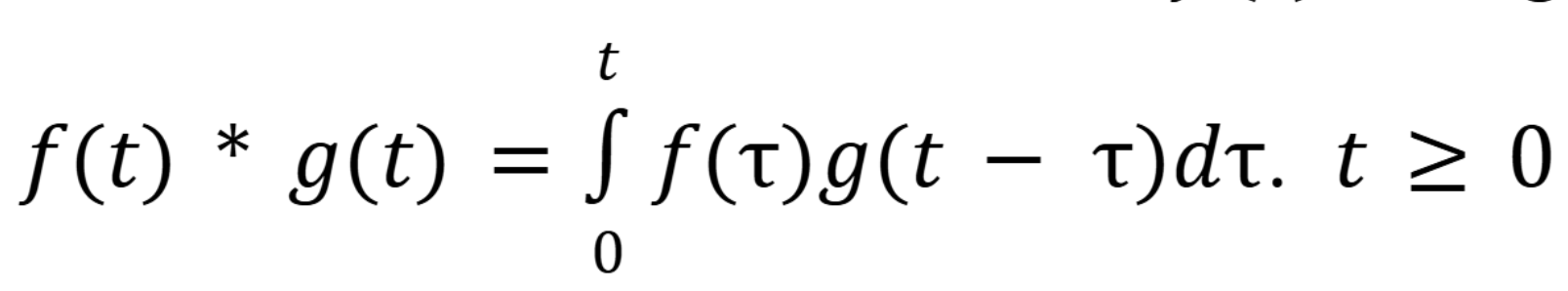
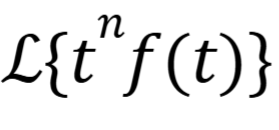
What is the image equal too

(November 14. 7.4) (Exam 4 Material).

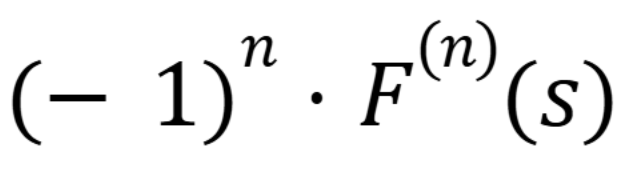
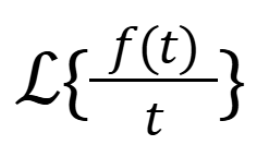
What is the image equal too

(November 14. 7.4) (Exam 4 Material).

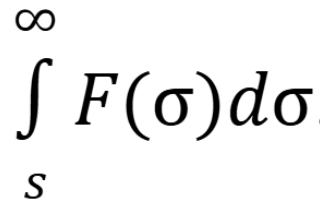
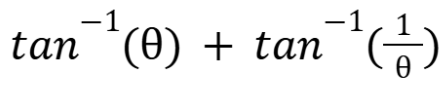
What is the image equal too

(November 14. 7.4) (Exam 4 Material).