6.1 LAW OF SINES 6.2 LAW OF COSINES and area of oblique triangle and herons Area formula

VERY IMPORTANT FOR CALCULUS

6.1 FLASHCARDS go FROM 1-

6.1 = This color

6.2=This color

VERY IMPORTANT=THIS

Overview= normal color

Derivation=THIS

Formula=This

Example=This

INTRODUCTION

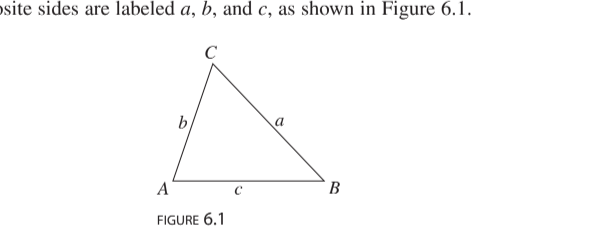
In Chapter 4 and in math before we have studied techniques for solving right triangles.

In this section and the next, you will solve oblique triangles—triangles that have no right angles.

Standard notation of Oblique triangles

Upper and lower case

The angles are labeled A,B,C upper case!!!!!!! and their opposote sides are labeled a, b,c lower case!!!!!!

WHAT YOU NEED TO KNOW TO SOLVE OBLIQUE TRIANGLES!!!

1. you need to know the measure of at least one side and any two other parts of the triangle—either two sides, two angles, or one angle and one side. This breaks down into the following four cases.

AAS/ASA

SSA

SSS

SAS

WHICH CASES LAW OF SINES AND ONES LAW OF COSINES

SUPER IMPORTANT

LAW of SINES
AAS/ASA

SSA

LAW of COSINES

SSS

SAS

AAS/ASA Case for solving

need to know two angles and any side

SSA case for solving

Two sides and an angle opposite one of them

SSS case for solving

Three sides

SAS case for solving

Two sides and their included angle

LAW OF SINES FORMULA

if ABC is a triangle with sides a,b,c, then

a/sinA = b/sinB = c/sinC

and the recipricol is sinA/a= SinB/b= SinC/c

Picture that shows law of Sines Proof Kind of

Reoriented acute and obtuse

Works for both ACUTE AND OBTUSE

1. ACUTE

Drop altitude -h (height)

Sin A= h/b so h=bsinA

Sin B = h/a so h=asinB

so they both equal h so

bsinA=asinB

so then divide both sides by SinAsinB and then get

a/sinA = b/sinB

1. Obtuse

Drop altitude -h (height)

Sin A= h/b so h=bsinA

Sin B = h/a so h=asinB

so they both equal h so

bsinA=asinB

so then divide both sides by SinAsinB and then get

a/sinA = b/sinB

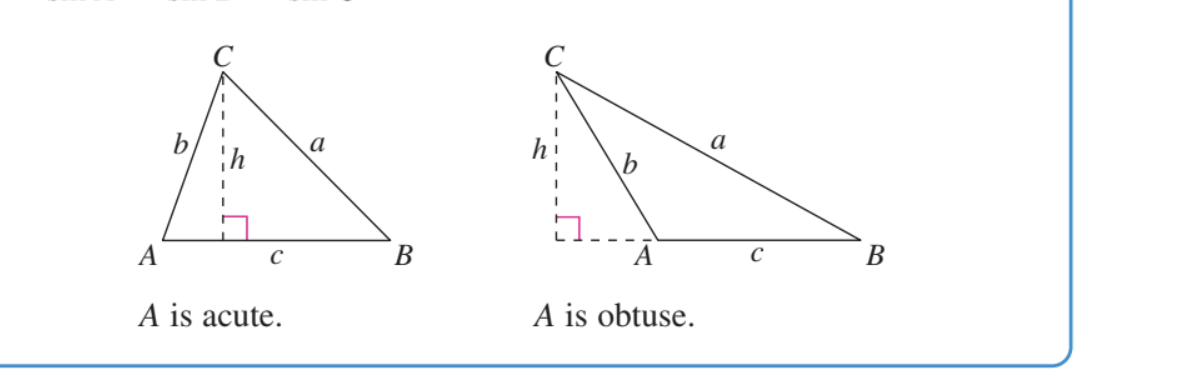
DERIVATION/PROOF OF LAW OF SINES

Make oblique triangles. The angles are labeled A,B,C upper case!!!!!!! and their opposote sides are labeled a, b,c lower case!!!!!!

can reorient triangle in tons of ways

A can be acute or obtuse

PROOF

Let h be the altitude of either triangle in the figure.

1. for A is acute

Then use sin identity to get

sinA=h/b or h=bsinA

sinB=h/a or h=asinB

then you can set equal because both equal to h and so bsinA=asinB

so then divide both sides by SinAsinB and then get

a/sinA = b/sinB

2. for A is obtuse

construct an altitude (h) from vertex B to side AC (extended in the obtuse triangle),

Then use sin identity to get

sinA=h/c or h=csinA

sinC=h/a or h=asinC

then you can set equal because both equal to h and so csinA=asinC

so then divide both sides by sinAsinC and then get

a/sinA = c/sinC

THEN BY Transitive Property of Equality you know that

a/sinA=b/sinB = c/sinC

LAW OF SINES

Example 1 Given Two Angles and One Side—AAS

How to do:

1. To solve 3rd angle A just know 180 degrees in a triangle and then subtract and get the missing angle.

Then to get the other 2 sides a and c do the law of sines

1. so you know b=27.4 and know all the angles so you know 3 parts of the equation To find A

2. a/sinA=b/sinB so then solve for a to get a= b/sinB (sinA) and then plug in numbers to get 43.06 feet for a

1. you also know 3 parts for C

2. c=b/sinB (sinC) and then plug in numbers and get 55.75 feet for c

Example 2 Given Two Angles and One Side—ASA

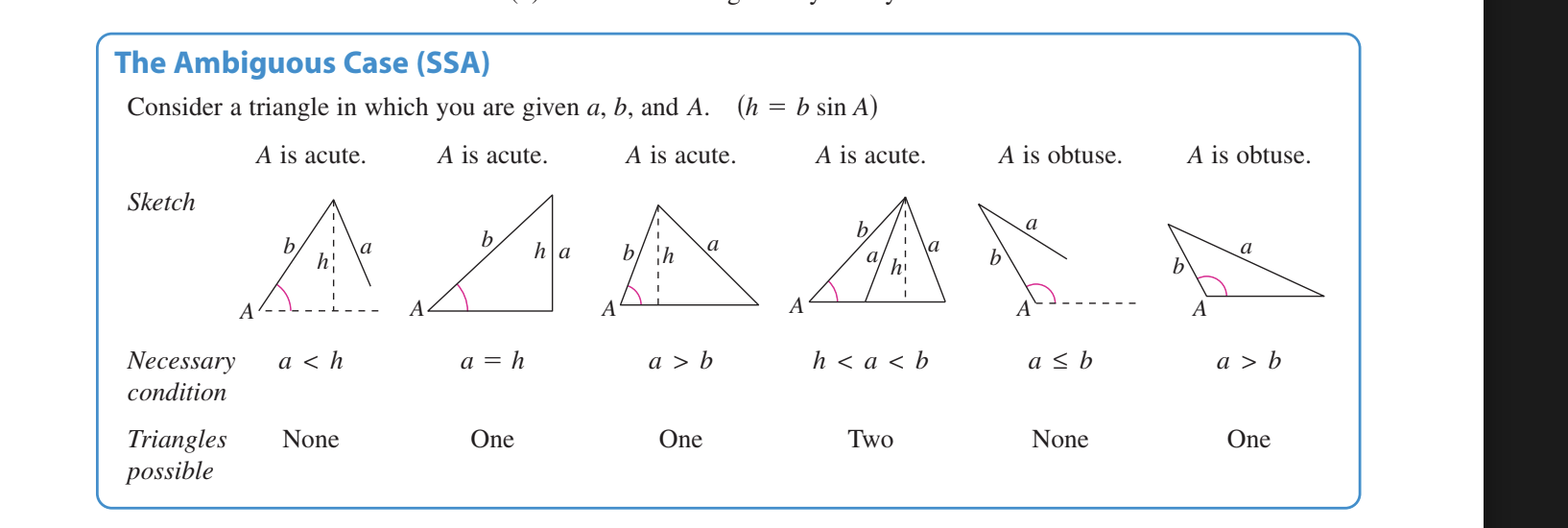
LAW OF SINES Ambiguous Case (SSA)

Two angles and one side determine a unique triangle.

However, if two sides and one opposite angle are given, three possible situations can occur: (1) no such triangle exists, (2) one such triangle exists, or (3) two distinct triangles may satisfy the conditions.

consider a triangle that you are given a,b, A

Key idea

Drop a height:

h=bsin⁡A

Compare side a to height h and side b

📐 If A is ACUTE

Condition	# of Triangles
a<h	0 (no triangle)
a=h	1 (right triangle)
a>b	1
h<a<bh	2 (ambiguous case!)

📐 If A is OBTUSE

Condition	# of Triangles
a≤b	0
a>b	1

🧠 Memory Tip

• Only SSA causes ambiguity

• Two triangles only when A is acute and h<a<bh < a < bh<a<b

Example 3 Single-Solution Case—SSA

Example 4 No-Solution Case—SSA

Example 5 Two-Solution Case—SSA

HARDEST ONE

Find 2 triangles for which a=12 meters, b=31 meters, A=20.5 degrees

By using law of sines

b/sinB=a/sinA so cross multiply to get aSin B= bsinA and then get sinB=((bsinA)/a) and then plug in the numbers and get sinB=0.9047

However from the unit circle sinB=.9047 has 2 solutions

Refrence angle of 64.8 degrees so B₁=64.8 degrees and B₂=115.2

SO THEN YOU SOLVE FOR REST OF STUFF USING THE ANGLE. HAVE TO SOLVE FOR ALL OF THE OTHERS FOR ANGLE 1 AND ALL OF THE OTHERS FOR ANGLE 2

1. B₁=64.8 angle solved

Solve for C So to get the angle C you do 180 degrees - 20.5 - 64.8 and get 94.7 degrees for C

Solve for c So to get side c you do the LAW OF SINES

c= a/sinA (sinC) and then plug in and get C=34.15 meters.

2. B₂=115.2 angle solved

Solve for C So to get the angle C you do 180 degrees - 20.5 - 115.2 and get 44.3 degrees for C

Solve for c So to get side c you do the LAW OF SINES

c= a/sinA (sinC) and then plug in and get C= 23.93 meters

LAW OF SINES Area of an Oblique Triangle How to get it

The procedure used to prove the Law of sines leads to a simple formaula for area of an oblique triangle

using the law of sines, the height of the triangle is

h=bsinA

the area of all triangles is

A=1/2 bh

This equals

A=1/2 (c ) (bsinA)

which equals

A= 1/2bcsinA

C is the base because on the normal orientation c is the base. bsinA is the hight of the triangle and you just put them together

LAW OF SINES Area of an Oblique Triangle Formulas

By different orientations you can get:

So the area of any triangle is one-half the product of the lengths of two sides times the sine of their included angle. That is,

Area= 1/2 bcsinA If you change orientation

Area=1/2 absinC if you change orientation

Area=1/2 acsinB

LAW OF SINES Area of an Oblique Triangle IF RIGHT ANGLE

Note that if angle A is 90 degrees then the formula gives the area for a right triangle:

Area=1/2bc (sin90) which sin90=1 so

A= 1/2 bc which is ½ base times height

The same results are also for B and C to equal 90

Example 6 Finding the area of a triangular lot

Plug into formula

6.2 LAW OF COSINES

LAW OF COSINES Introduction

Two cases remain in the list of conditions needed to solve an oblique triangle—SSS and SAS. If you are given three sides (SSS), or two sides and their included angle (SAS), none of the ratios in the Law of Sines would be complete. In such cases, you can use the Law of Cosines.

6.2 Proof of law of Cosines

set up a normal triangle with the standard notation of oblique triangles.

Then you drop an altitude and solve for the inside right triangle with B as the angle

Then for the height of the triangle h you get asinB because when you do sinB you get sinB=h/a and then h=asinB

Then for the base of the triangle which is c for the right side of the base right of the altitude you get acosB because you do cosB you get cosB=x/a and then x, which is the side of the small triangle to be x= acosB

You know the base is c so the 2 parts that are cut off by the altitude equal c so then the other side left of altitude is c-acosB because the 2 peices of the base have to add up to c and c-acosB + acosB =c

Then you do the pythagorean theorem for the left inside triangle which has side lengths c-acosB (left side of c), asinB (height), and b as the hypotenuse

you get

(c-acosB)² + (asinB

you do