Physics 2212 test 3 conceptual for true false

south pole to north pole

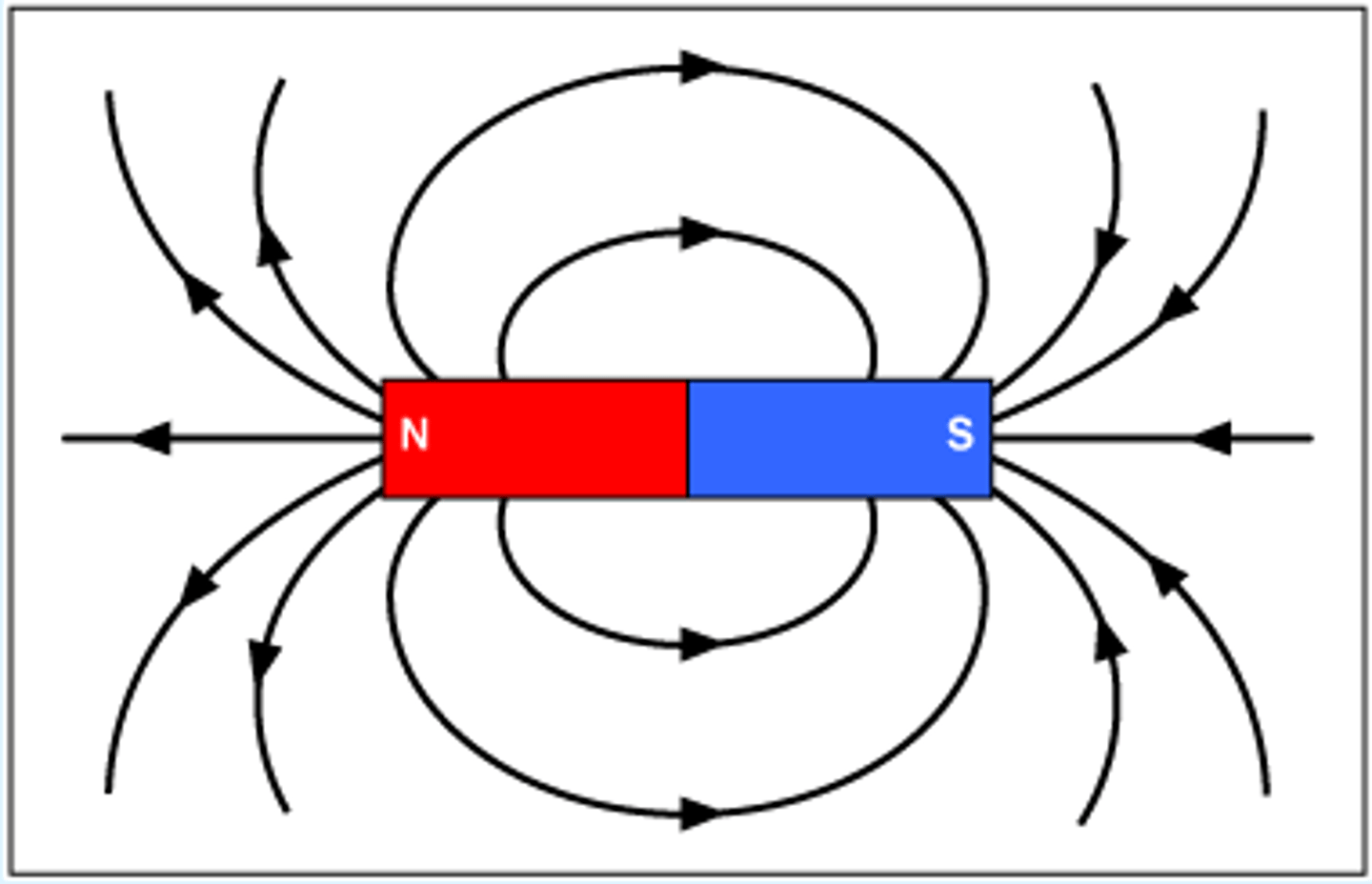
dipole moment points like this

current loops

these produce a magnetic field/force and torque that can orient a compass needle

electric field

this of a point charge: electric field or magnetic field

has distribution depends on the velocity

|A| |B| sin(theta)

cross product - magnitude wise

non-vero velocity

point charge needs to have this in order to exert a magnetic field

zero

value of cross product if two vectors are parallel

Tm/A

unit s of mu-not/4pi

any shape

a loop of current of this shape can generate a b-field

north to the south

magnetic field points this way in a bar magnet

superposition

just like e-field this princple of b-fields holds true - they are not subject to influence by other b-fields

decreases

magnitude of B does this as you move further from the wire carrying current

current never abruptly stops

why is the concept of carrying a current delta(L) unfeasible?

direction of current

direction of the b-field is determined by the

south to north

magnetic dipole points in this direction

spin and angular momentum

electrons have these two properties that help it generate a magnetic field - first one is bigger

ferromagnetic

materials have dipoles aligned in thesame direction in small patches. When a magnetic fieldis applied, these patches align, creating a macroscopicB field that can last for a very long time

like cobalit, iron, etc

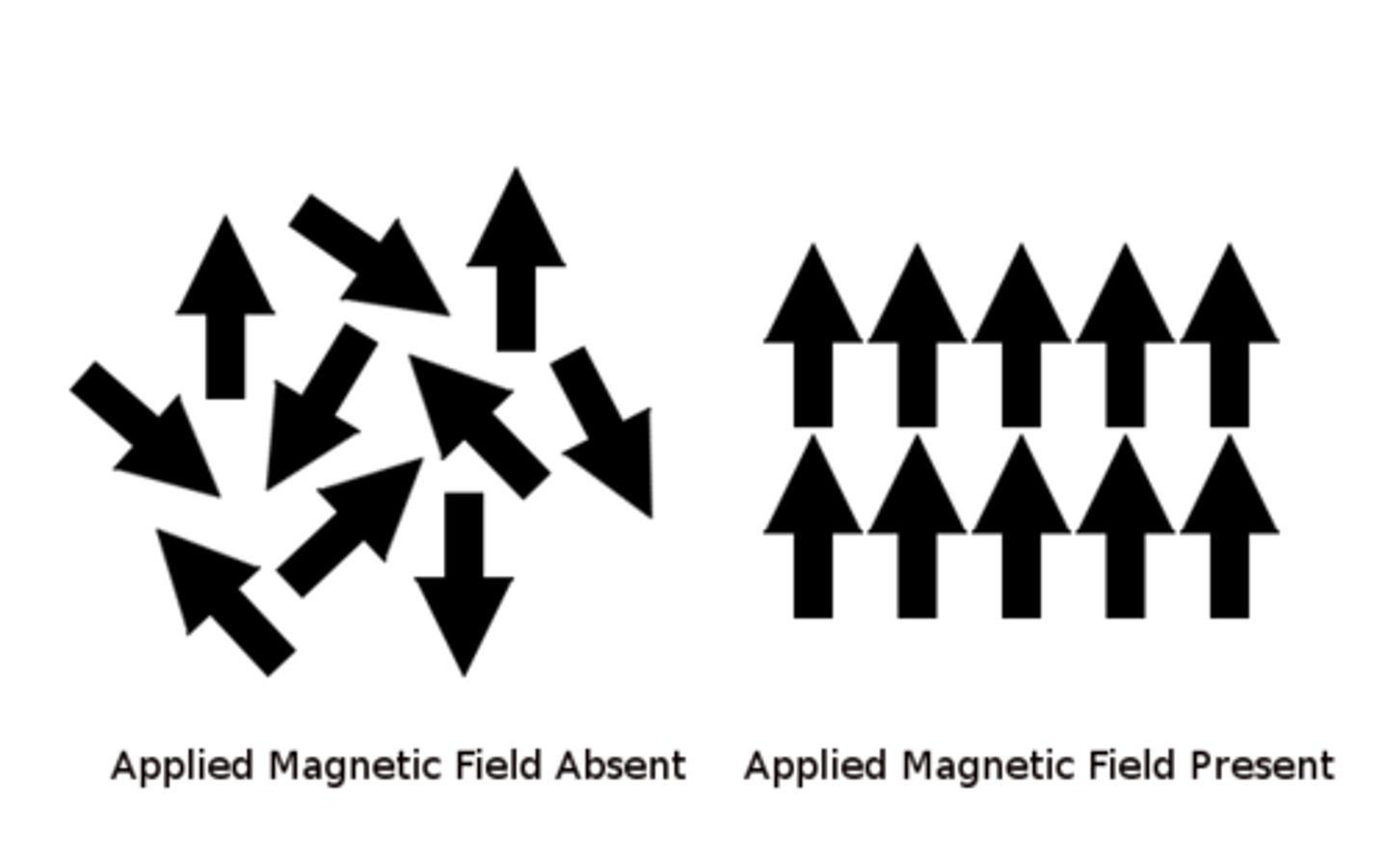
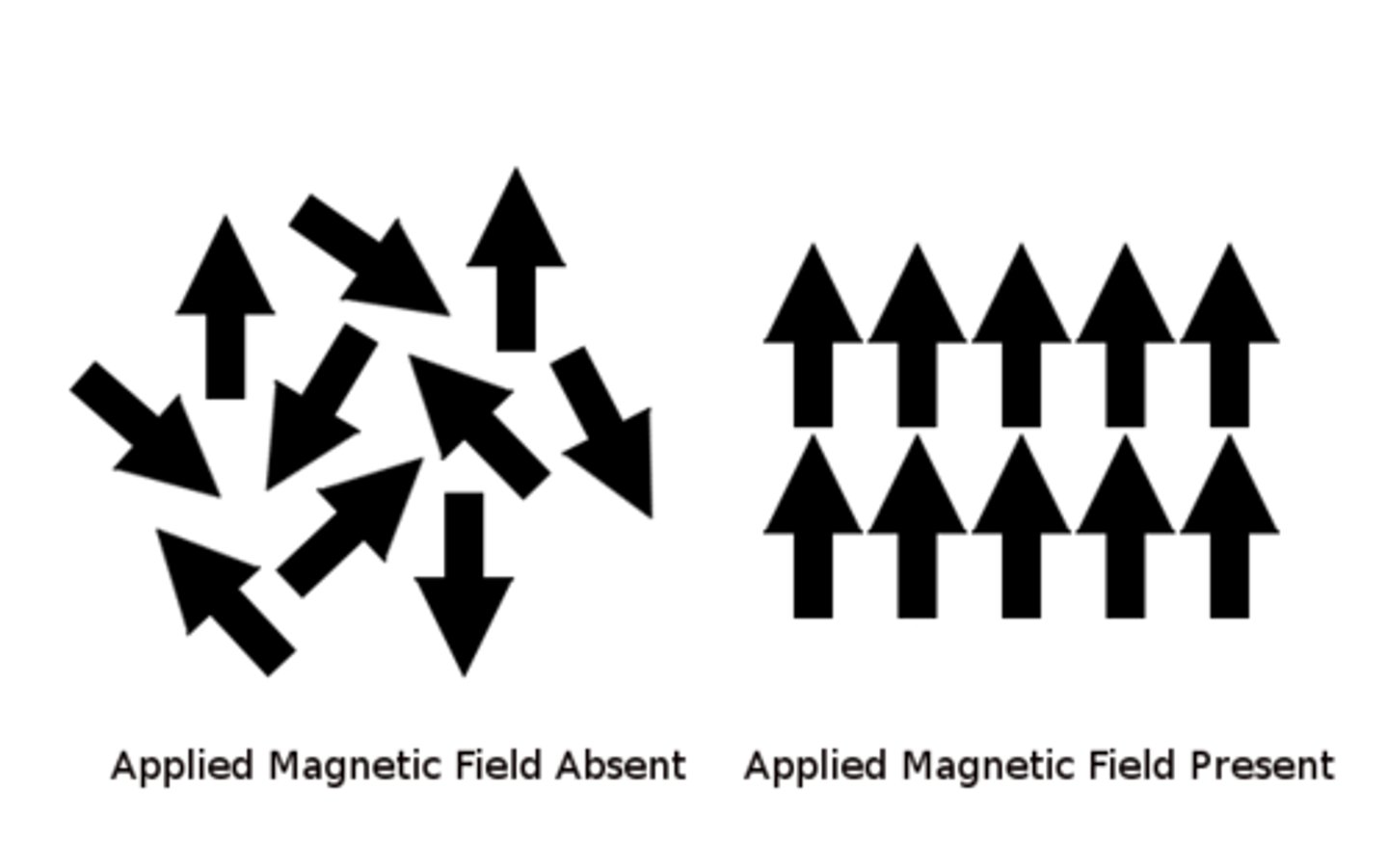
paramagnetic

materials have dipoles that can betemporarily aligned in an external B field, but areoriented at random otherwise

aluminum, titanium

Curie's Law

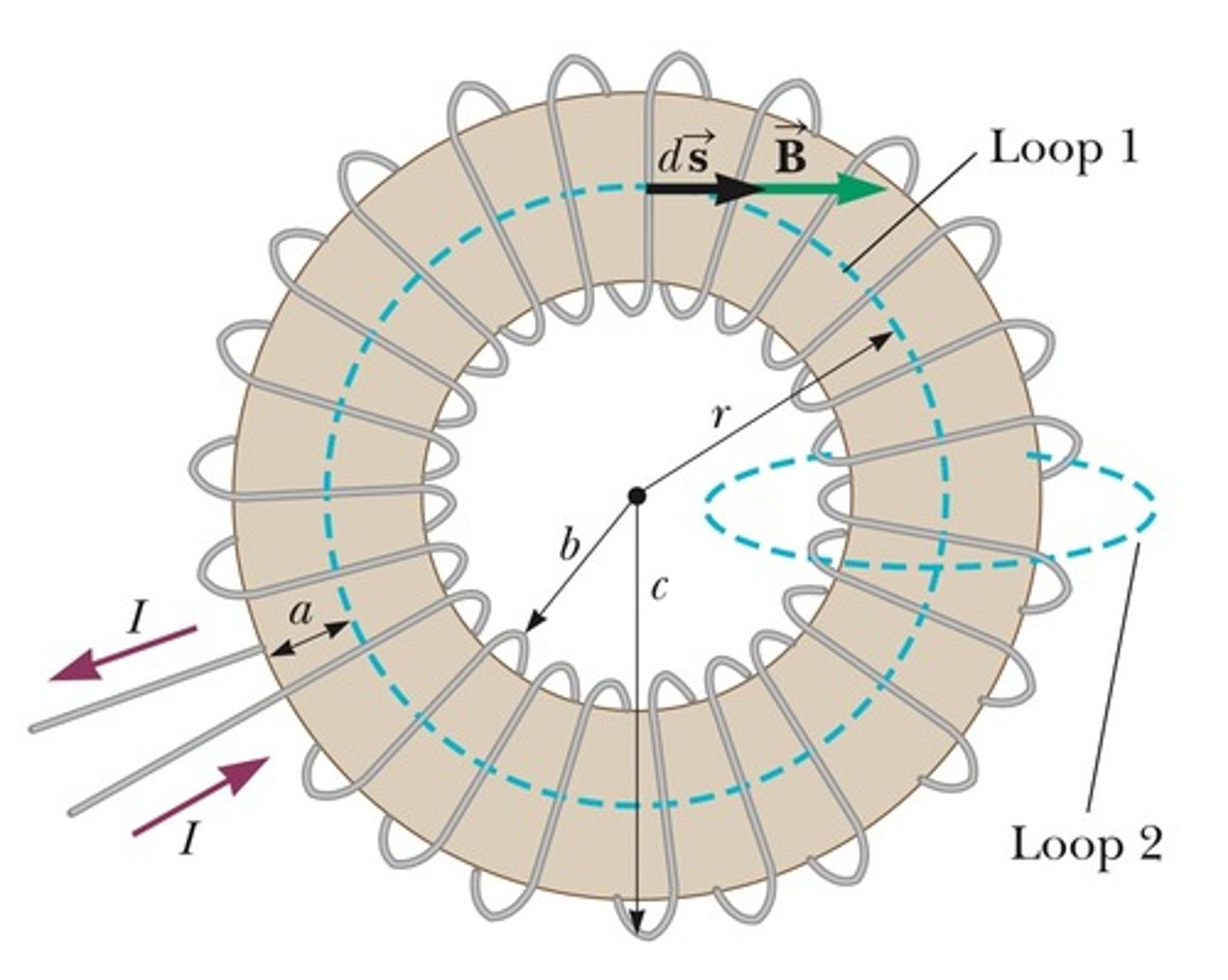
the 𝐵 field has the same symmetries as the infinite wire that produces it. Here, rotational symmetry and translational symmetry.

electric dipole field

when r<

constant, 0 (negligable)

the magnetic field inside an infinitely long solenoid is this, magnetic field outside of an infinitely long solenoid is this

constant, looks like a dipole

the magnetic field inside an finitely long solenoid is this, magnetic field outside of an finitely long solenoid is this

mv^2/r

in perfect circular motion of a charged particle - can set the magneti force equal to this

do this in cyclotron motion

lorenz force

sum of the electrostatic and magnetic forces acting on a body

F = Eq + qvxB

cyclotron motion

The circular motion of a charged particle in the plane perpendicular to a magnetic field - will set mv^2/R equal to the magnetic force

identical/even spacing

in order to use solenoid formula for b-field, this must be present between the rings

dipole moment, mu

only factor affecting magnetic field very far from the closed circuit/bar magnet

toroid

current that wraps around itself

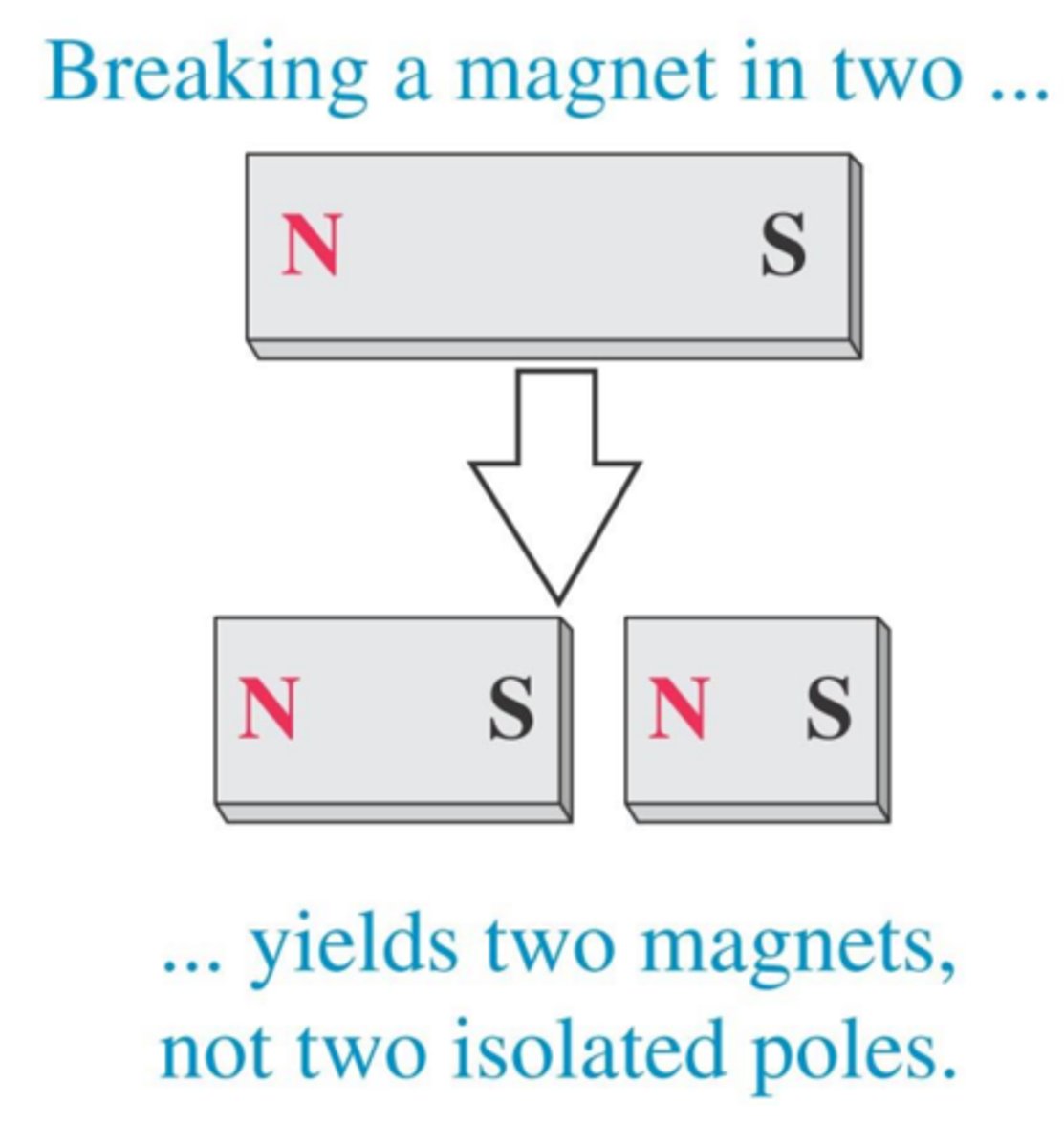
magnetic monopoles

because these do not exist, if you chop a magnet in half you will still get a north and south end

high temperature

this can destroy ferromagnetism

repeled

two parallel currents running opposite to each other will be attracted or repelled?

antiparallel currents

attracted

two parallel current running linearly/same direction to each other will be attracted or repelled?

parallel currents

zero

magnetic of magnetic force on a magnetic dipole bar magnet/coil in a uniform magnetic field or any closed loop of current

zero

work done by a magnetic force on a charged particle in cyclotron motion or a current loop in a uniform magnetic field - as the force can only change the direction not the magnitude of velocity

Hall effect

The phenomenon by which a force is brought to bear on a moving electron or hole by a magnetic field applied perpendicular to the direction of motion. The force direction is perpendicular to both the magnetic field and the particle motion directions.

The Hall Effect occurs when electrons moving through a conductor experience a magnetic field, resulting in a perpendicular force (Lorentz force).

In response, electrons drift to one side of the conductor, creating an excess negative charge on that side and leaving an excess positive charge on the opposite side. This separation of charges generates an electric field, known as the Hall electric field, which balances the magnetic force, eventually stopping further charge separation.

As a result, measuring the voltage across this conductor (the Hall voltage) allows determination of properties like charge carrier density and the magnetic field strength. This phenomenon provides an important practical method for sensing magnetic fields and characterizing materials.

no

is there electric current inside of a bar magnet

spin of electrons

this creates the dipole moment for a bar magnet

Antiferromagnetism

A form of magnetism in which unpaired electron spins on adjacent sites point in opposite directions and cancel each other's effects.

V and B

two things we can change to alter the Lorenz Force for a point particle

torque

a magnetic field does not exert a net force but it exerts a net this on a magnetic moment/dipole

mu in direction of B

torque stops rotating magnet when this is achieved

charged particle moving through magnetic field never does work on a moving point charge

relationship between magnetic field, charged particle, and work

zero

magnetic force on a current carrying wire in a closed loop in a uniform magnetic field

use I*deltaL x B

magnetic force on a current carrying wire that is straight in a uniform magnetic field

perpendicular

normal vector is alligned like this to an area's surface

no

do charges outside of a Gaussian surface contribute to the net flux?

Gauss's Law

total electric flux through a surface equals charge enclosed Q divided by epsilon knot

the Q enc

flux remains constant as long as this remains constant in Gauss's law

will not matter if on or off center

exit the volume

every magnetic field line that enters the volume must also:

Gauss's Law for Magnetism

Magnetic flux through closed surface is zero because individual magnetic poles have never been observed

enclosed magnetic poles will always cancel to 0 - no separation

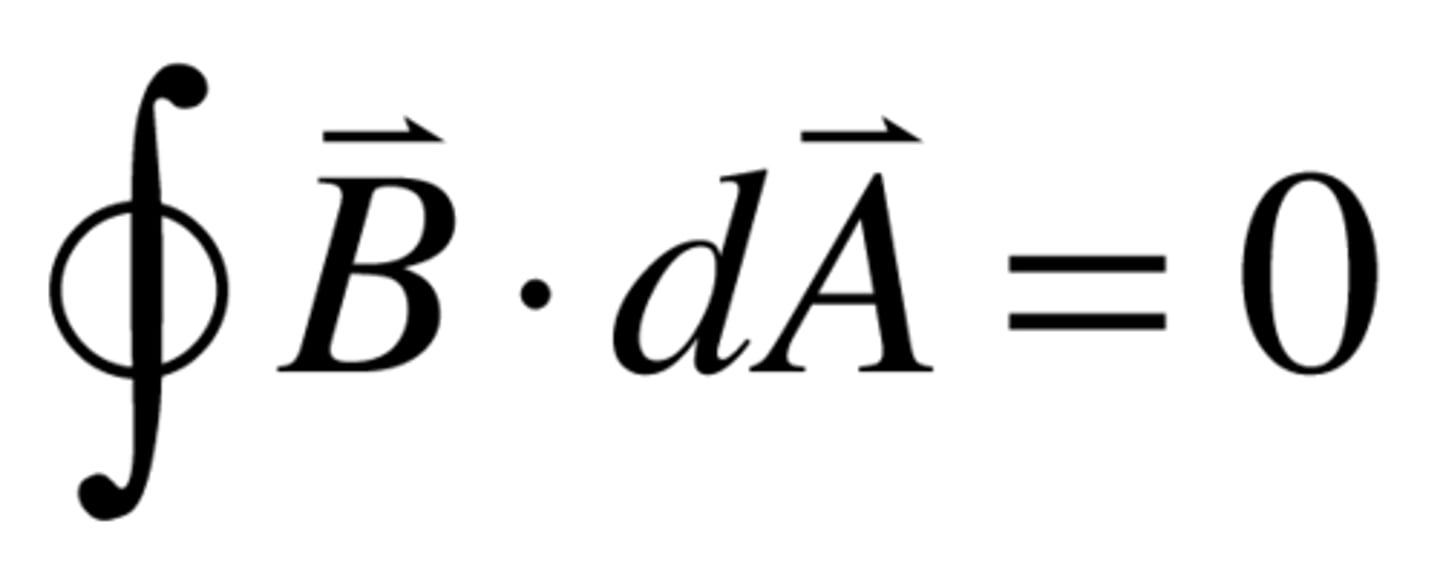
zero

value of total magnetic flux through a closed surface

non-Coulomb electric field

The electric field due to changing magnetic fields.

closed loop is not zero voltage

lenz's law

The induced current flows in a direction so as to set up a magnetic field to oppose the change in magnetic flux

the negative in faraday's law

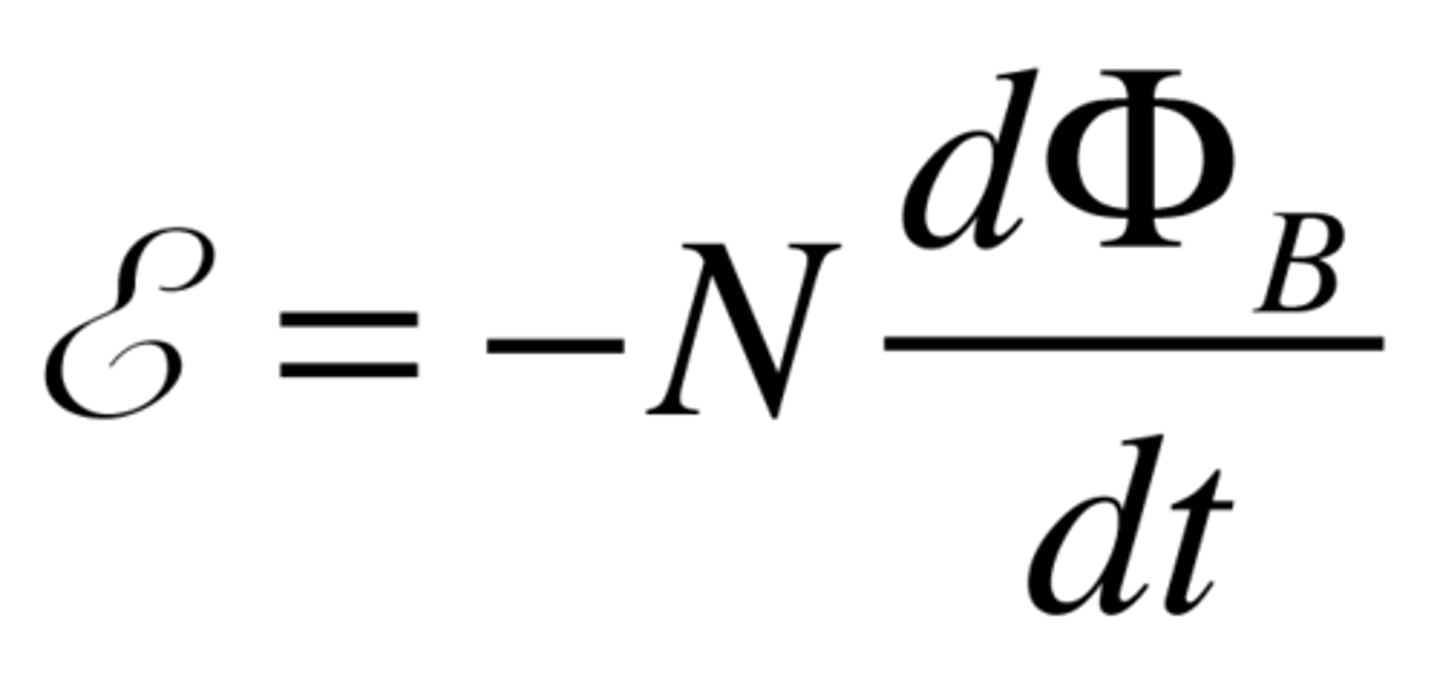
faraday's law

An electric field is induced in any region of space in which a magnetic field is changing with time.

induced current

current in a circuit due to a changing magnetic field

possible due to the non-coloumbic electric field wrappign around the perimeter

same time

if you drop bar magnet through copper pipe with southside down or northside down what will move through the tube faster

1) can guess direction of E.

2) Have near constant E

two paramater's fr Gauss's law

enclose the charge

Gaussian surface must do this

non-coloumbic e-field + emf

what is made from a time derivative in magnetic flux (change in flux)

closed loop integral not equal to zero

what is unique about the non-coloumbic electric field

current is independent to number of loops in a coil

relationship between the induced current and number of loops in a coil

solenoid

A very long coil of wire that produces a magnetic field when carrying an electric current

constant b-field inside of it

Faraday's experiment

Closing the switch in the primary circuit induces a current in the secondary circuit BUT only while the current in the primary circuit is changing

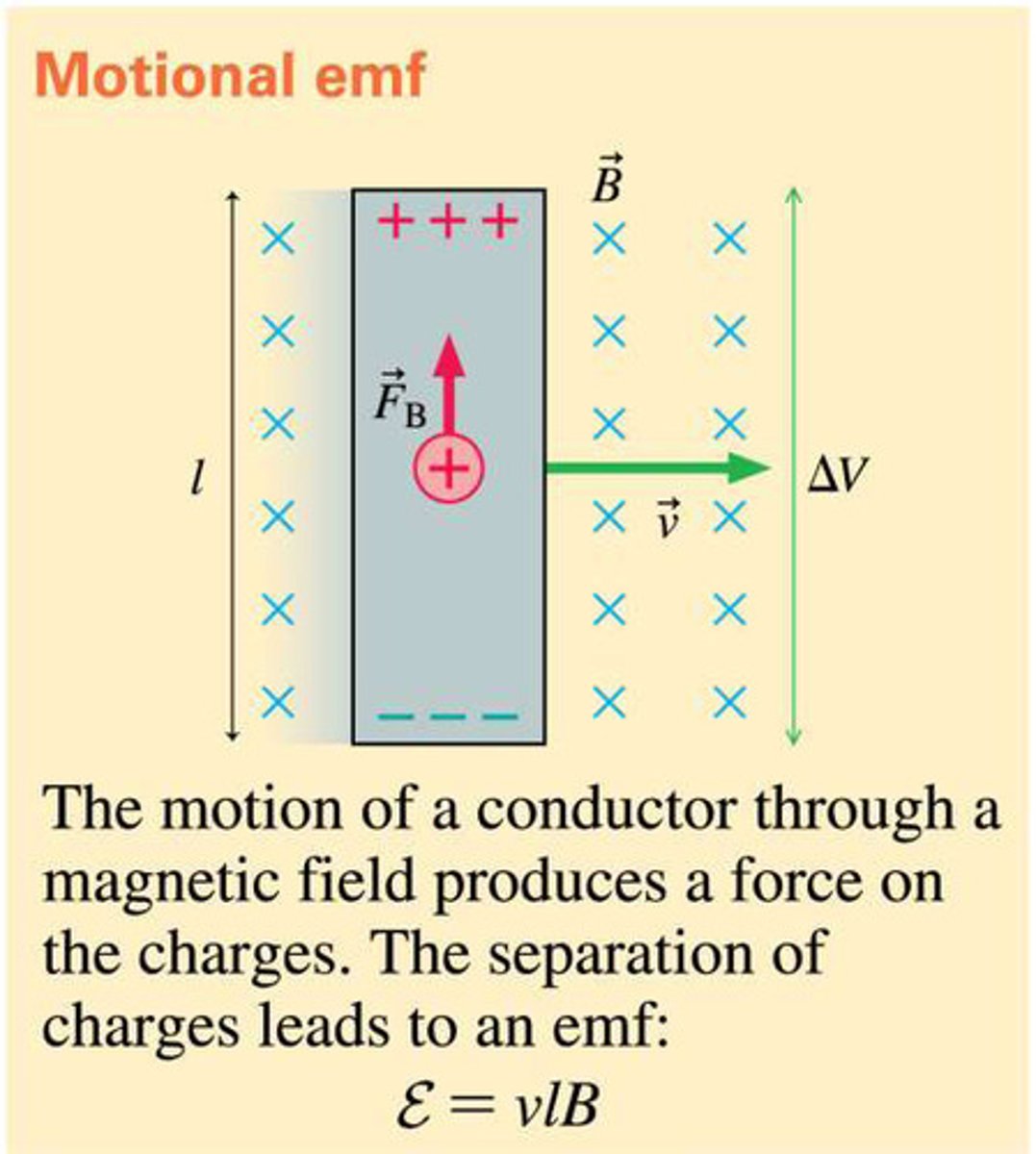
motional emf

The emf produced across a conductor due to its motion through a magnetic field - associated with change in surface

can have a conductor act as a battery

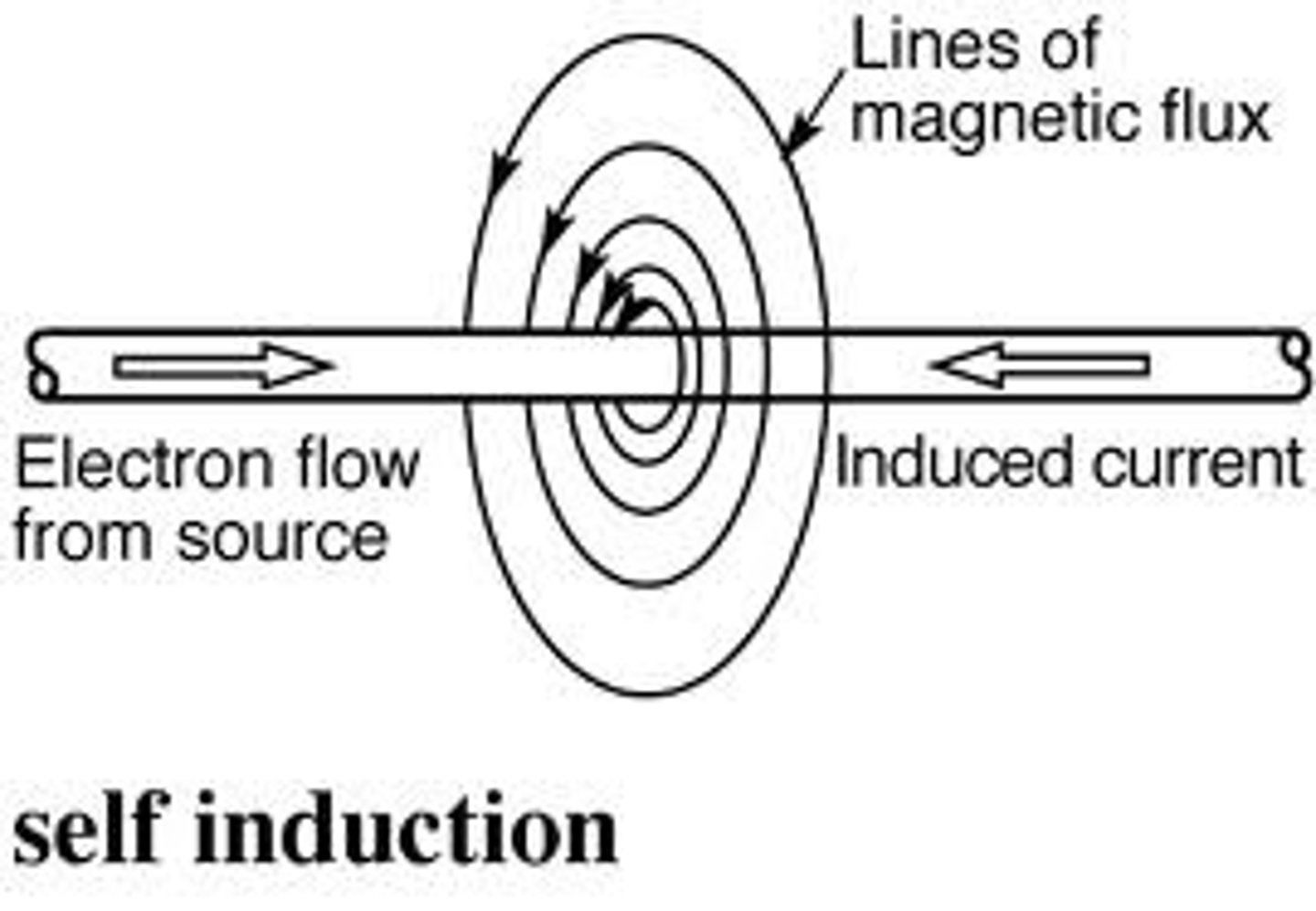
self-inductance

tendency of a conductor to oppose changes in the current flowing through itself

ex: decrease magnetic flux out of the page by decreasing counter clockwise current - nature now makes self-induced counter clockwise current to counteract the original change!

enclose

in order to have change in flux due to a solenoid, the area of interest must do this to the solenoid

true

if change in b-field remains constant than induced current also remains constant

transformer emf

compared to motional emf - this emf is associated with a change in B-field rather than a surface

L * dI/dt

formula for back inductance or the change in current through a solenoid over time

number of turns in a solenoid

ratio of voltages in transformers is equal to this

-mu * B

formula for rotational work/change in potential enegy in a magnetic field of a magnetic dipole

this is a dot B