8. Dynamic games of incomple

The Beer Quiche Game

• Nature makes the first move selecting whether a person is strong or weak with 0.5 probability

• Player 1 learns their type and decides to order a beer or quiche — player 2 doesn’t know the type

• Player 2 observes what player 1 orders, and upon observing what they order decide if they want to start a fight or stay still (they have an information set — player 1 has chosen Beer or Quiche, but they don’t know which type they are)

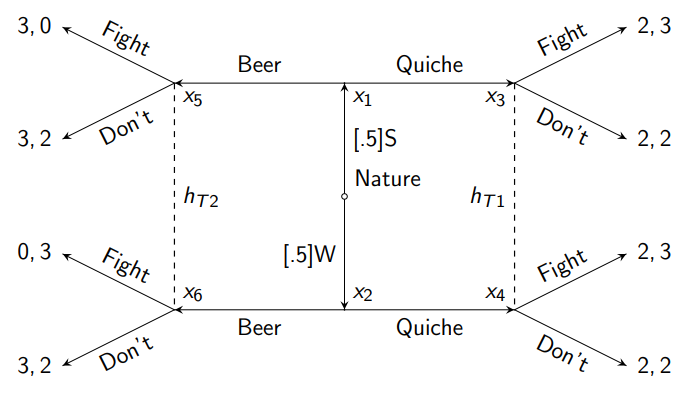
The Bayesian normal form of the Beer Quiche game

How are normal form payoffs calculated?

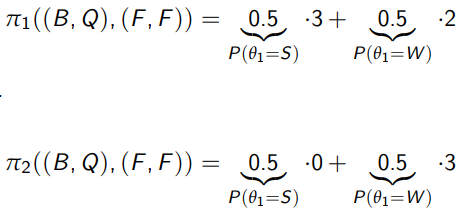
What role do observable actions play?

• The strategy of player 1 might change dependent on the type of person that they are

• A player might only choose a beer if they are a strong type — player 2 could know from this observation that player 1 is strong, which will influence their decision to fight or not

• In this way, players can update their beliefs about the type of the other player in the game and thus change their probabilities

Systems of belief

• A player might update their beliefs about the other player so that the probability player 2 assigns to player 1 of being type x is updated at each node

• For each information set h, µ(x) is the probability assigned to being at a specific node x

• If these probabilities are well defined at the nodes, then a game has a system of beliefs

  • A system of beliefs µ of an extensive-form game assigns a probability distribution over decision nodes to every information set

    • That is, for every information set h ∈ H and every decision node x ∈ h, µ(x) ∈ [0, 1] is the probability that player i who moves in information set h assigns to his being at x, where x∈h µ(x) = 1 for every h ∈ H

What is Bayesian updating?

• This is when probabilities are updated based on the actions other players have taken; players update their beliefs about types and strategies

• P(t_i = θ_i |a_i) = P(a_i |t_i = θ_i)P(t_i = θ_i) / P(a_i) = P(a_i |t_i = θ_i) / P(a_i) · P(t_i = θ_i)

• This is the probability that an agent plays an action given they are of a certain type, divided by the probability of any type performing that action, multiplied by the probability of a certain type occurring

  • This only works for on-path information sets; we can only update beliefs about a type when we actually observe an actions; actions which don’t occur are unobservable

How does sequential rationality work in Bayesian games?

• Sequential rationality is embedded in the notion of updating our beliefs; we best respond given the information we have available

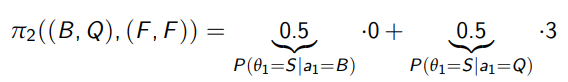
What is a Perfect Bayesian Equilibrium?

• A Bayesian Nash Equilibrium strategy together with a system of beliefs µ, computed using Bayes Rule where possible (i.e. on path), constitutes a perfect Bayes Equilibrium if each player plays a best response given their beliefs at each information set

• Obviously, there are no restrictions under this method on off-path beliefs

• A perfect Bayesian equilibrium can be realised if all information sets are induced to be realised by the strategy; in a game where a person chooses to enter if competitive and stay out of a market if weak, then from entering or staying out of the market the player can discern the type and thus best respond

• A PBE can only be realised by finding a set of beliefs which supports off-path behaviours

  • When players pick different actions dependent on their type, this is pretty straightforward, but if an action is chosen by all types, one must find the set of beliefs which supports the equilibrium

Calculating PBE

• We need to first construct the payoff matrix based off of the probabilities of nature

• We can then update our beliefs about players types based on different strategies; if we know a player will only enter the market when they are strong, and will stay out of the market when weak, then upon observing a market entry, we know that the player is strong

  • Bear in mind we only need to evaluate the candidates which are NE under the natural probability weightings

• We can then calculate the payoffs given these new probabilities to find the PBE

Why does SPNE not work in games of incomplete information?

• A NE is subgame perfect iff, in every proper subgame, the restriction of the strategies to that subgame is a Nash equilibrium in the subgame, on or off path

• However, in games of incomplete information, because players do not know the types of other players, they are always uncertain and thus their information sets are combined, meaning the only proper subgame of a game is the entire game

  • Thus, every Nash Equilibrium survives subgame perfection

How are consistent beliefs defined?

• A profile of strategies σ* = (σ₁*,..., σ_n*), together with a system of beliefs µ*, is consistent if there exists a sequence of nondegenerate mixed strategies, {σ^k}^∞_k=1 , and a sequence of beliefs that are derived from each σ^k according to Bayes’ rule, {µ^k}^∞_k=1 , such that lim_k→∞(σ^k, µ^k) = (σ*, µ*)

How do consistent beliefs constitute a sequential equilibrium?

• A profile of strategies σ* = (σ₁*,..., σ_n*), together with a system of beliefs µ*, is a sequential equilibrium if (σ*, µ*) is a consistent perfect Bayesian equilibrium