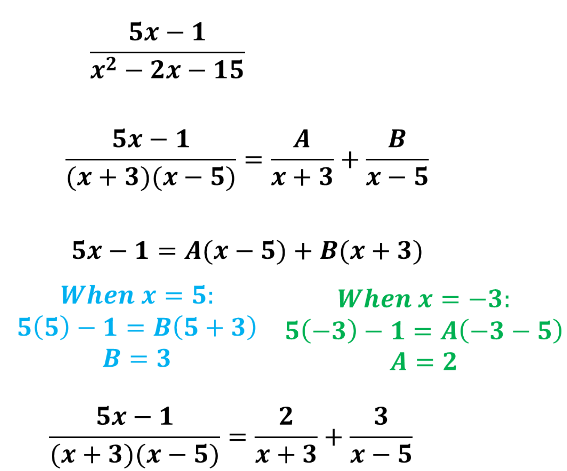Chapter 7 Main Ideas

The Order of a Matrix

the number of rows times the number of columns

ex: 2 × 3

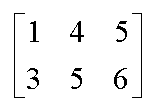
Matrix Multiplication

Multiply each number in the row of the first matrix by each number in the the column of the second matrix and add together each solution; this is done repeatedly until all rows and columns are done

Identity Matrix

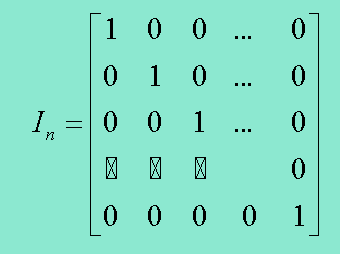
Determinant of a Matrix

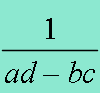
Inverse of a 2 × 2 Matrix

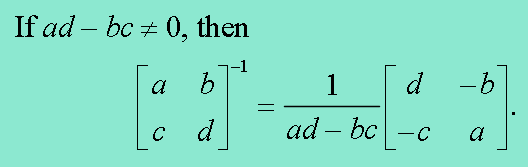
Triangular Form of a Linear System

Solving a system of multiple equations for one variable then imputing that variable back into it to solve for another variable until all variables are found.

Gaussian Elimination

Using operations to produce an equivalent system of linear equations which can be added and subtracted from each other to solve for a variable.

Row Echelon Form of a Matrix

Using operations to produce equivalent matrices which can be added and subtracted within each other to solve for all variables. The matrix should have descending 1’s from the top left corner of the matrix with 0’s below each 1.

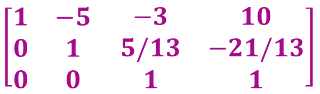
Reduced Row Echelon Form

If we continue to apply elementary row operations to a row echelon form of a matrix, we can obtain a matrix in which every column that has a leading 1 has 0’s elsewhere.

Partial Fraction Decomposition

Breaking up the denominator of a function into its factors and solving after elimating a variable.