MMW PRELIMS (terminologies only)

jeckole is real // study the material too & how to solve

Mathematics

• Formal system of thought for recognizing, classifying, and exploiting patterns. The origins of counting.

  Ex. Geometric patterns, wave patterns in water and on land, patterns of movement, fractals

with curiosity and desire to know the truth

How is Mathematics done?

Everyone

Who uses Math?

Leonardo Bonacci (Fibonnaci)

Most talented mathematician of the middle ages

Liber abaci

Fibonnaci’s book?

The Fibonacci Sequence

1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144

Language

A systematic means of communicating by the use of sound or conventional symbols. It is the code we all use to express ourselves and communicate to others.

Mathematical Language

English Language

Constants (fixed values)

What does the start of the alphabet mean?
ex: a,b,c

Positive integers (for counting)

From i to n?
ex: i,j,k,l,m,n

Variables (unknown)

End of the alphabet?

ex: ….x,y,z

Nouns

Could be fixed things, such as numbers, or expressions with number

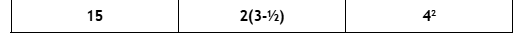
Verb

Could be the equals sign “=” or an inequality like < or >

Pronouns

Could be variables like x or y

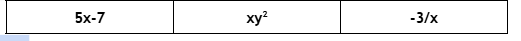
Sentence

When put together, a Mathematical Sentence would look like this:

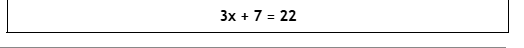
similar

~ means?

Congruent

≅ means?

Same Shape

Similar means?

Same Size and shape

Congruent means?

Phrases

Expressions

Sentences

Equations or Inequalities

Translating English into math

This ability requires recognizing the verbal phrases that translate into mathematical operations.

Addition

 is the answer to an addition problem

• Added to

• (the sum of) 

• (the total of)

• Increased by

• Plus

• More than

Subtraction

is the answer to a subtraction problem

• Subtracted from 

• (the difference between)

• Less 

• Decreased by 

• Minus

• Less than

  Does not possess the commutative property .

  
  

Minuend

first number

Subtrahend

second number

Multiplication

is the answer to a multiplication problem

• Times

• The product of

• Multiplied by

• Of 

• Twice

Division

 is the answer to a division problem

• Divided by

• The quotient of

• The ratio of

  Does not possess the commutative property .

Power ( aⁿ )

• The square of (a²)

• The cube of (a³)

Equal

• Equals

• Is/Are/Was/Were

• Amounts to

• The result is

• To obtain

Inductive Reasoning

• Uses patterns to arrive at a conclusion (conjecture)

• From specific to generalities

Examples: 

1. Every quiz has been easy. Therefore, the test will be easy.

2. The teacher used PowerPoint in the last few classes. Therefore, the teacher will use PowerPoint tomorrow.

3. Every fall there have been hurricanes in the tropics. Therefore, there will be hurricanes in the tropics this coming fall.

Deductive Reasoning

• Uses facts, rules, definitions, or properties to arrive at a conclusion

• From generalities to specific

Examples:

1. The catalog states that all entering freshmen must take a mathematics placement test. 

You are an entering freshman.

Conclusion: You will have to take a mathematics placement test.

1. 90% of humans are right handed. Joe is human, therefore Joe is right handed

Precise

accurate, unambiguous expressions, strict and exact

Concise

consistent, brief and efficient expression, use of symbols & notation

Powerful

expression of complex thoughts, analysis and solution of problems

PEMDAS

Describes the order of operations, starting with Parentheses (Groups), Exponents, Multiplication or Division, and Addition or Subtraction.

1 + 2 × 3 (6 - 4 ÷ 2)

= 1 + 6 (6 - 2)

= 1 + 6 (4)

= 1 + 24

= 25

Product Rule

when multiplying like terms, add the exponents

x3 • x2 = x3+2 = x5

x3 • y2 = x3y2 ← not like terms

Quotient Rule

when dividing like terms, subtract the exponents

x3 ÷ x2 = x3-2 = x

Power of a Power Rule

when raising a power to a power, multiply the exponents

(x3)2 = x3×2 = x6

Power of a Product Rule

when raising a group of factors, all factors are raised to the exponent

(xy)² = x²y²

Zero Exponent Rule

values raised to zero are equal to 1

  xyz⁰ = xy

(xyz)⁰ = 1

Finite Set

{a,b,c}

Infinite Set

{a,b,c,...}

Types of Relations

• one-to-one

• one-to-many

• many-to-one

• many-to-many

Functions

Can only have a relation of one-to-one and many-to-one

Closure Property

When two real numbers are added, the result will also be a real number

2 + 3 = 5

Commutative Property

• Reversing the order of addition or multiplication will not affect the result

 2 + 3 = 3 + 2

(2)(3) = (3)(2)

Associative Property

Changing the grouping of numbers for addition or multiplication will not affect the result

(2 + 3) + 4 = 2 + (3 + 4)

(2 × 3) × 4 = 2 × (3 × 4)

Identity Property

A number multiplied by 1 or increased by 0 remains equal to itself

78 + 0 = 78

78 × 1 = 78

Distributive Property

When a number is multiplied to a group of two added values, multiply the outer number to each value in the group

3 (x + 2) = 3x + 6

Inverse Property

For each real number, there exists a unique number for its inverse

9 + (-9) = 0

9 × 1/9 = 1

“Everything has a counter move that cancels it out.”

Division

Binary to Decimal Uses?