Statistical analysis

Sample?

• used to draw conclusion about one or more characteristics of a population

• representativeness is important

What is the null hypothesis?

• its about the mean in the population

• h0

What is the T statistic?

• used to determine whether the null hypothesis is rejected or not

Standard error?

• uncertainty around estimate

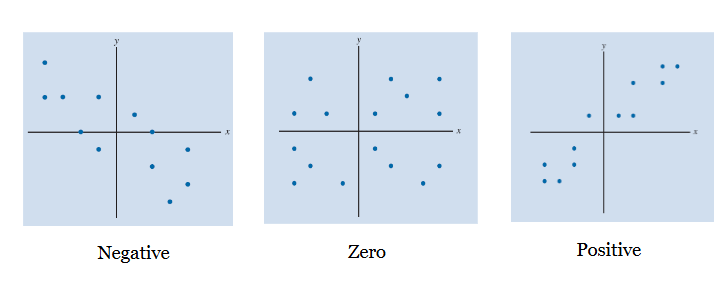
Scatter plot patterns

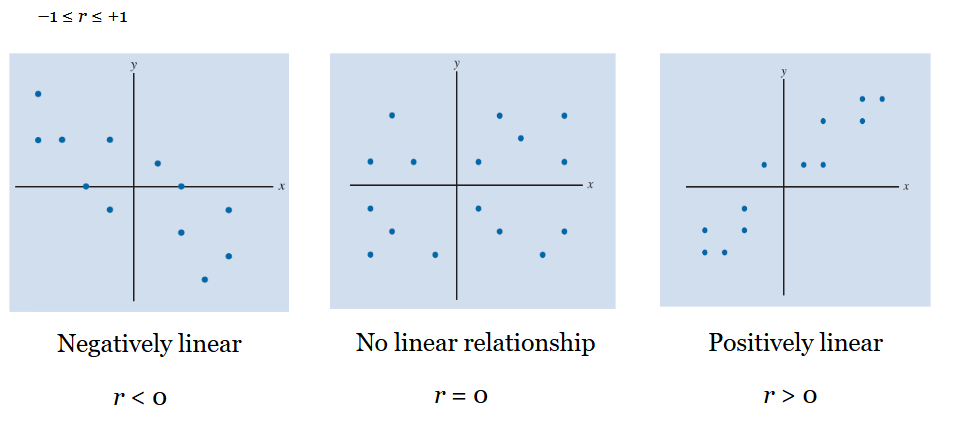
Correlation patterns

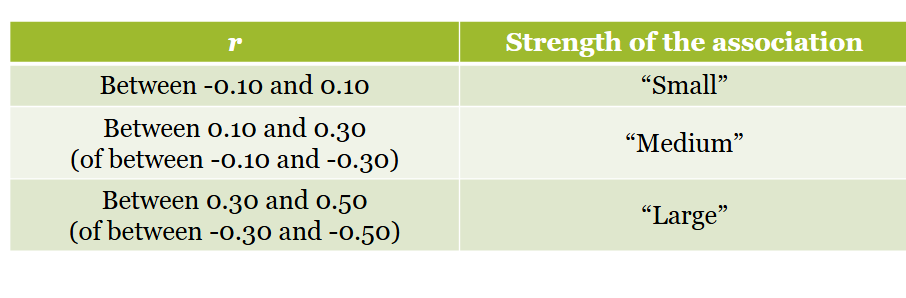
Correlation coefficient

• closer to -1: more strongly the variables move in the opposite direction

• closer to 1: more strongly the variables move in the same direction

Regression analysis

• What is the effect of the IV on the DV

• What is the relationship between the sales of my product and the properties of my locations?

• DV/Y is predicted by IV/X

  • DV to be explained

  • IV the explanator

Ordinary Least Squares/OLS

• the line of best fit

• a smaller amount of predicting errors

• how close are the residuals to the regression line → shows you the line with the least amount of prediction errors possible for a straight line

Linear regression model

• make predictions within data or outside of it

• can summarise how predictions or average values of an outcome vary across observations defined by a set of predictors

• y = value based on fitted line + distance from fitted line

  • y = β0 + β1x + ε

  • We say that y is related to an intercept (constant), a variable x and an error term

β0 and β1 are the parameters

• These need to be estimated

• β1 provides information about how y and x are related to each other → what regression models do

Interpreting linear regressions

• Small p-value: evidence for a significant relationship between x & y → interpret the coefficient

• Large p-value: no evidence for a significant relationship between x & y → don’t interpret the coefficient

Binary variables

• variable that takes either of two values

Including in regression analysis

• Process: Transform into a “dummy” or “indicator” variable where one category = 0 and the other = 1 (if not already 0/1 scaled) and include that variable in your model

  • The 2 categories have numerical values of 0 or 1

R2/ R squared

• Percentage of the variation in y that is explained by x

• Between 0% and 100% (e.g. 28%)/ number between 0 and 1 (0.2)

• a goodness of fit measure

• tells us how much the fit of model is improved

• indicates the % of variance in the DV that the IV can explain collectively

• Higher R2 = better the model fits the obs

  • More variance = data points are closer to the line

  • line is steeper, reduce variaton

  • x helps to predict y

Causality

• how does the change in X affect Y

• if one goes up the other goes down

• Correlation is not causation

why is the diff between correlation and causality so important

• useful to establish causality to know what the causal effect of the variable is

  • medical world

  • policy: impact of policy change, can mean

ways to establish causality

• experiments, treatment and control group, measure a certain outcome and compare it

Causal claim

• a direction

• X is doing something to Y

  • are associated/correlated/related

Non causal claims

• no direction or specification which of X & Y goes first

• talking how the variables work together

Reverse causality

• Y to X

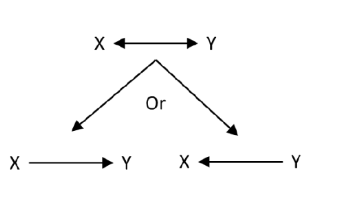
Omitted variable

• Z is related to X & Y and plays a big role

Logistic regression

• to predict a categorical outcome 1 VS 0

• This is better than linear because probabilities are assumed instead of 0 and 1 only

• used to predict categorical variables

• s line makes sure that we have predictions between 0 and 1

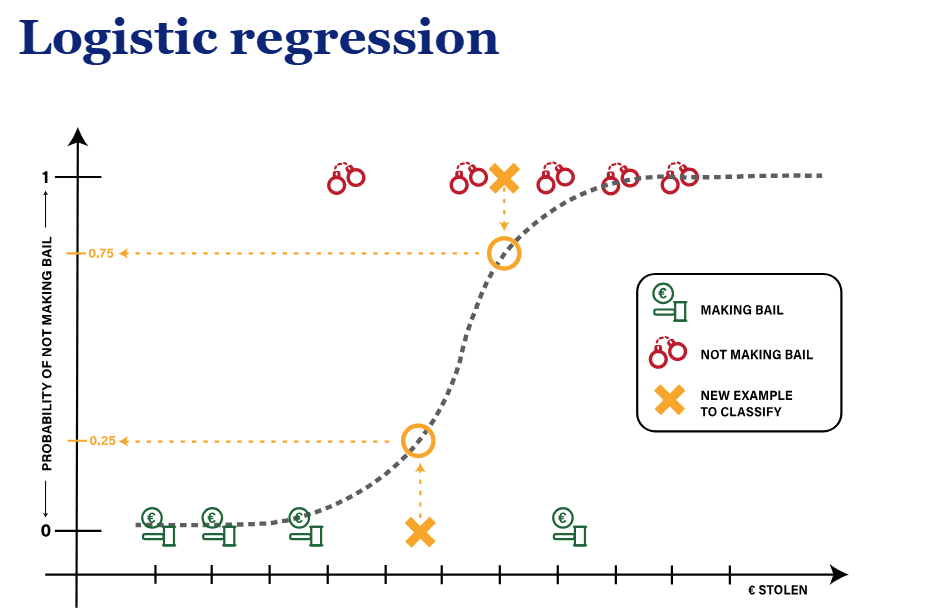
Interpreting logistic regression

• 1 DV and multiple IVS

• Positive: we expect Y=1 to become more likely as X increases

• Negative: we expect Y=1 to become less likely as X increases

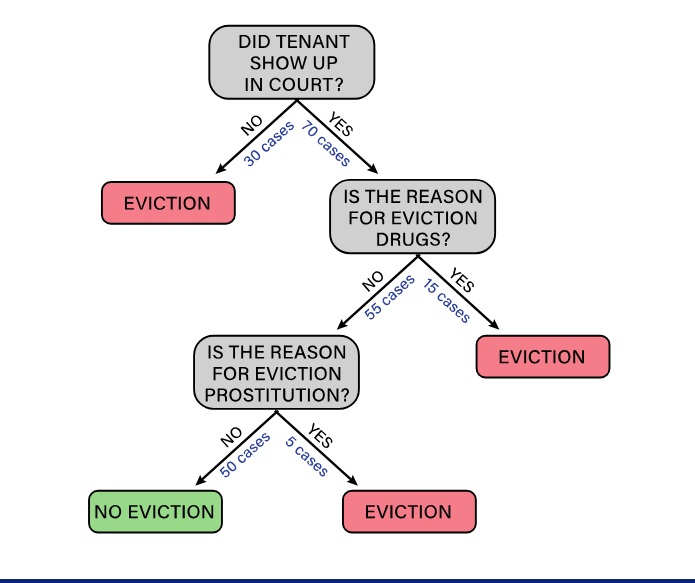
K nearest neighbours

• focus on indi and look in database and look for the similar indi, and look at the neighbours, copy the outcome to the indi

• x and y axis could be anything

• based on characteristics and compare the indi to everybody else in the database, and place them accordingly → find the b persons similar to A, and find the most similar 3 → is it always 3? closest to A

• make prediction on A, depending on the probability of neighbours at least 50%

• based on a circle

• K is the basis of the comparison

• depends on the domain tho

• For k we determine the percentage of points that belong to category 1 (e.g., eviction)

• At least 50%? → Classify as category 1

• The new example is ALWAYS placed after

how large K should be?

• depends on the prediction performance of your model

• does it change a lot

  • messing with diff k values what outcome are there

• what is the predictive power of a smaller K → can miss patterns: overfitting

• too big: can miss trend

  • trading off process, need to find the balance

SVM?

• support vector machines

• searching for hyperplane line that separates the 2 groups as well as possible by looking for a border house closest to the line on both sides

• goal: make the distance as large as possible and can separate the groups properly → if as far as possible, good job

• domain specific

• Depends on the characteristics of the data set, needs to be able to separated

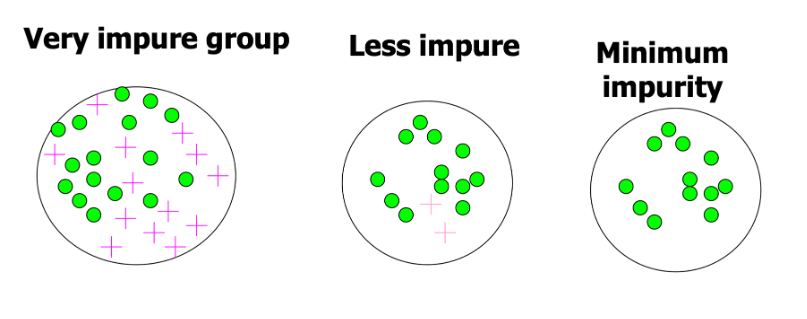
Decision tree

oal of decision tree is go from very impure to minimum impurity

to arrive at the final tree, 1/0

Impurity

• measure of heterogeneity, how mix is the data at each step

• Impurity has maximum value (= 0.50) when the observations are evenly distributed among the categories (50% in category 1; 50% in category 0)

• Impurity is 0 when all observations belong to 1 category (100% in either category 1 or category 0

• It decreases from Impure to Pure

• pluses and circles - mixture of both

• categories

very impure

• 50 of each

• max impurity

• max value of .5

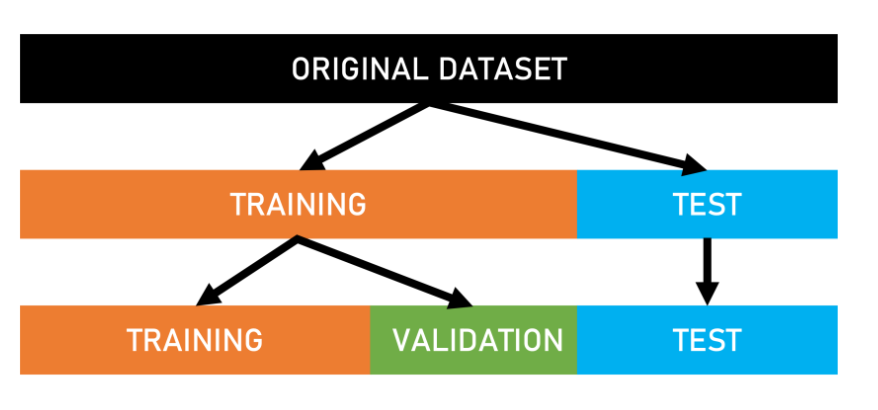
Training and testing

• Prediction is probs the most interesting phase

• testing set is used for prediction purpose

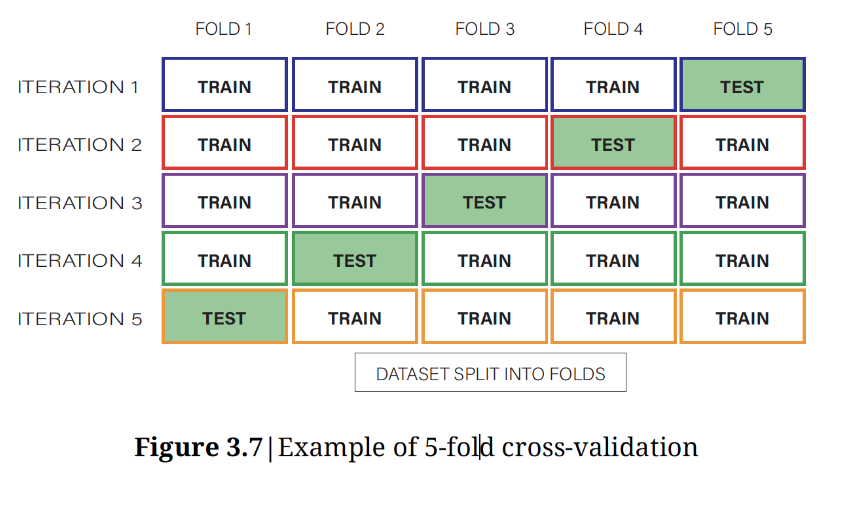
K fold cross validation

• way to evaluate the model’s performance

K fold cross validation process

• take all available data for training model & split set into k parts

  • divide dataset in 5 parts

  • the first 4 is 80, test is used to predict → based on iterations

  • take one part out and train the model using the remaining k-1 parts

  • trained model is compared to labels & actual labels with withheld parts

  • repeated till each k withheld part is done

• full use of data for prediction

• cross validation is used

  • determine the optimal parameters of the system

Accuracy

• percentage of true positives and true negatives

Sensitivity

• percentage of true positives within category 1

Specificity

• percentage of true negatives within category 0

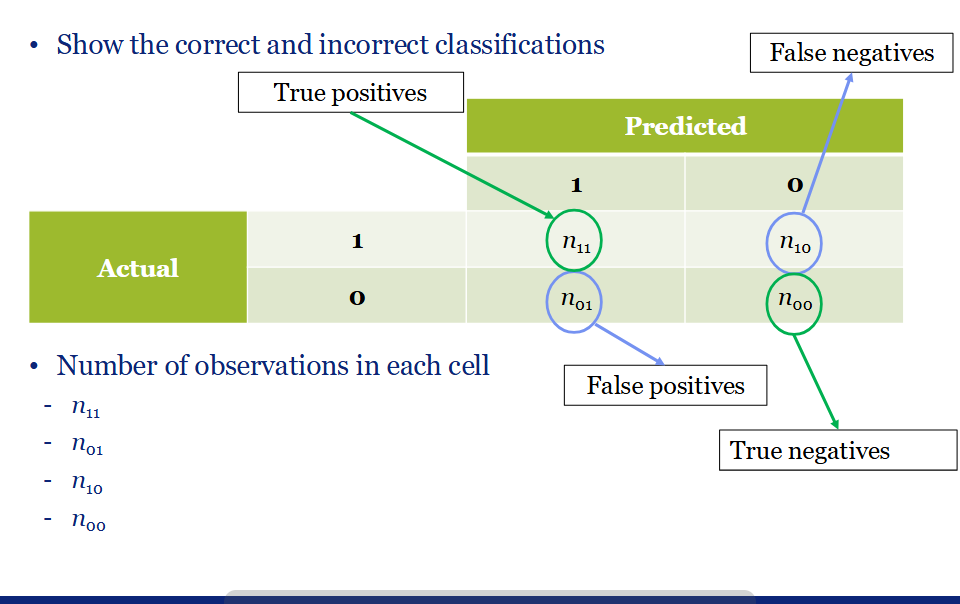
Model evaluation: confusion matrix

• it shows the correct and incorrect classifications

• looks at the no. of observations in each cell

In practice for confusion matrix

• 1/0 variable, compare to predicted values

• false negative → predicted 0 and when its supposed to be 1

• false pos → does not match reality

• true neg and pos are the ones we care about good prediction, add them together and divide by total no of obs → accuracy

• always interested in high accuracy? if so , why or why not

• always use true pos and neg together and compare it to the total

recall/precision/f1score

• checks whether if 1s are predicted well

recall formula

• true pos / true pos + false pos

Precision formula

• true pos/ true pos + false neg

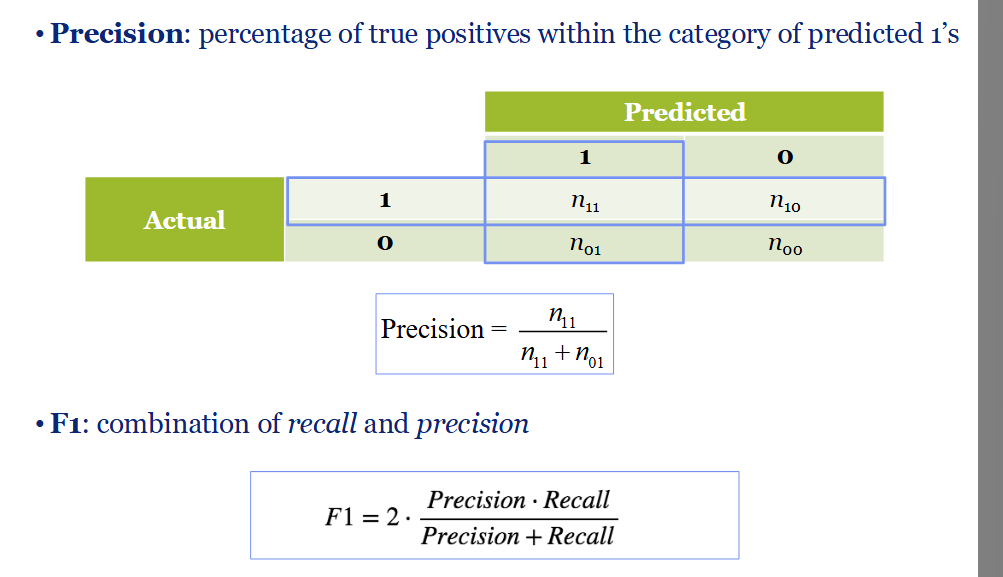
F1 score

• used to evaluate performance

• a harmonic mean between precision and recall

F1 formula

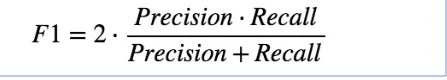
Precision and F1

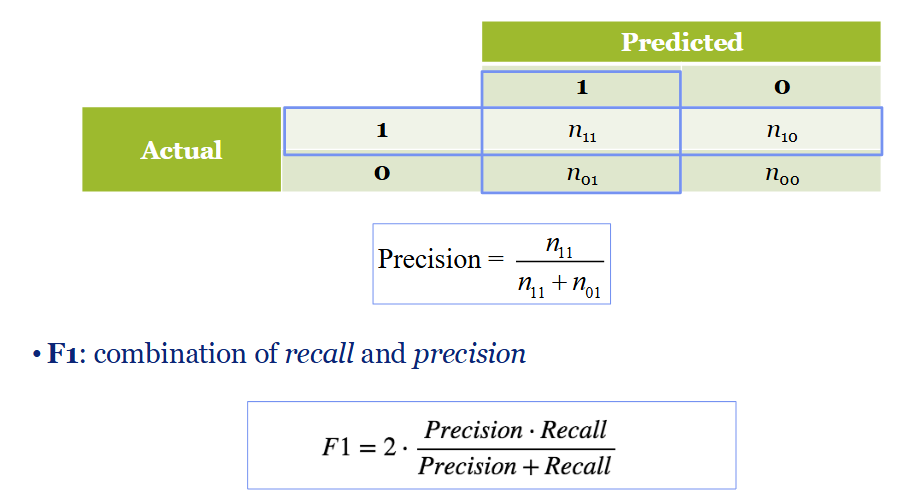
• Precision: percentage of true positives within the category of predicted 1’

• the percentage of cases with a specific outcome classified correctly by the system

Process of precision

• predicted and actual case outcomes compared

• True positive: the known truth of the actual value → need it: MATCHES

  True negative: actual value is saying I don’t need it

  False neg: actual value is telling is me I need, but model is saying I dont

  False pos: what the model predict is not real

Accuracy

• general measure of prediction quality

• counts the no of correctly predicted observations divided by total number of observations

Formula

• True pos + True neg / all obs in the table

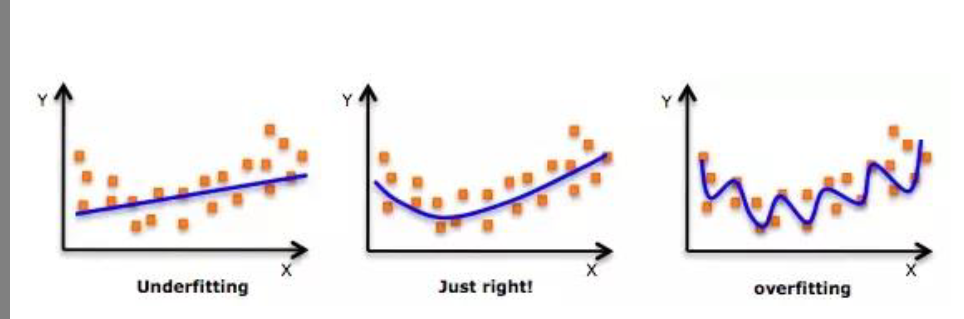
Overfitting

• the model explains very well but does not predict we