Unit 8 - Confidence Intervals

point estimator

a statistic that provides an estimate of a population parameter
ex: p̂

point estimate

the numeric value of the point estimator/statistic (from a sample)

ex: 0.5

C% confidence interval

gives an interval of plausible values for a parameter

write as: point estimate ± margin of error

general formula: statistic ± (critical value * SD of statistic)

interpret confidence interval: “We are C% confident that the interval from [] to [] captures the true [population parameter in context]”

-if procedure repeated many times (get all possible samples), C% of the resulting confidence intervals would contain the pop parameter [thing you're measuring]

-probability that the confidence interval captures μ is either 0 or 1, but we don't know which _{^{(either does or doesn’t capture μ)}}

-"n% confidence interval" -> n% does NOT mean probability/chance

_{^{*the difference btwn the point estimate and the true parameter value will be less than the M.o.E. in C% of all samples (will be w/in the interval in C% of all samples)}}

how to get margin of error _{^{(population proportion)}}

what margin of error does/doesn’t account for

critical value _{^{(t* or z*)}} * SD of the statistic _{^{(the SE since uses p̂ or x̄)}}

_{^{(margin of error for pop proportion or mean is critical value * SD of statistic)}}
z* x √[(p̂(1-p̂)/n] ← for pop. proportion
M.o.E. affected by SE (standard error) (z* or t*, n, s_x)

-

accounts for random sampling error (variability when take multiple random samples)

DOES NOT account for sample biases (e.g. nonresponse, undercoverage)

confidence level C

gives the overall success rate of the method for capturing the true parameter

interpret confidence level: "If this method of constructing confidence interval was repeated many many times, about C% of the confidence intervals will capture the true [population parameter in context]"

_{^{*take many samples of the same size from [this population], the method would yield an interval that captures the true parameter value in C% of all possible samples (of many confidence intervals)}}

!!! why 95% → large enough to be correct while still keeping precision (don’t want useless/unnecessary #s)

ex: 99% means larger critical value/z-score, so larger margin of error, so wider confidence interval (less risk of incorrect b/c wider interval includes more #s)

-smaller C% confidence level -> smaller z*, smaller M.o.E., narrower confidence interval

-larger C% confidence level -> larger z*, larger M.o.E., wider confidence interval

get confidence intervals of two #s, one w/in shaded area and one outside shaded area

-both intervals same length

-within: contains the pop. parameter

-outside: doesn’t have pop. parameter

_{^{SD depends on sample size n; critical value depends on confidence level and sampling distribution of the statistic}}

incr n (sample size)

decr n (sample size)

-decr SE _{^{(the SD)}}, more precise/smaller M.o.E. → narrower confidence interval

-incr SE _{^{(the SD)}}, larger M.o.E. → wider confidence interval

-both do NOTHING to confidence level/correctness

Conditions to check before calculating confidence interval for p _{^{(population proportion)}}

• Randomness (ex: SRS)

• 10% condition (n≤1/10*N)

• Large Counts condition (np̂ ≥ 10 AND n(1-p̂)≥10)

_{^{use p̂ b/c don’t know p (if knew p, wouldn’t be estimating confidence interval)}}

standard error

when the SD of a statistic is estimated from data
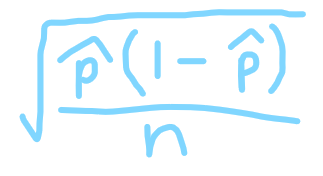
(pic for SE of sample proportion - don’t know p, so use p̂ to get SD of statistic)
SE of sample mean is s_x/(√n) - don’t know σ, so use s_x

z* vs. z-score

• how we bound our confidence interval _{^{(for pop. proportion)}}

• - and + value (from center, so same value diff sign, ex: -0.1, 0.1)

• aka critical value; specifically used as the bounds for a confidence interval

vs.

• how many SDs away a value is from the mean for any value

—both use SD away from the mean aka center

!!! 95% confidence from Normal curve, use ‘2’ from empirical rule → actually 1.96 SDs away from mean

question w/ someone claiming a % → check if percentage/proportion is in C% confidence interval. if not, it is not plausible (since interval gives the plausible values of p)

include units for numbers!

confidence interval given (a, b) -> point estimate aka statistic is right in the middle. M.o.E. is the difference btwn this middle # and the endpoint

poll has margin of error r% and C% confidence level, means that the poll used a method that gets an answer within r% of the truth abt the population C% of the time

Formula to get C% confidence interval for an unknown proportion p

‘C% of its area is btwn -z* and z*’

p̂ is sample proportion

z* is from C% confidence

n is sample size

right of (±) is the margin of error

_{^{❕show work by putting formula and plugging #s}}

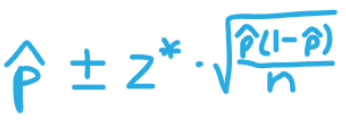
4 Step Strategy to answer Confidence Interval Questions

• State - what is the population of interest? What parameter (e.g. p) do you want to estimate? What is your confidence level?

• Plan - check conditions

• Do - make calculations

• Conclude - interpret confidence interval w/ context from the problem

What to do if you don’t know p̂ and need to estimate it

use p̂=0.5
_{^{(margin of error is largest when =0.5)}}

How to get sample size n that will yield a level C confidence interval for a population proportion p w/ a maximum margin of error of M.E.

gives M.o.E. as a percentage (put as decimal), p̂, and C% (use to find z*)

divide both sides by M.E. so just on left, multiply both sides by √n so just on right

square everything and solve for n

always round UP to nearest whole number _{^{(since n must be greater than or equal to the # you calculate)}}

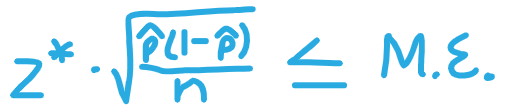
How to get confidence interval w/ calculator for pop. proportion

Interpret confidence interval

[stat] ‘Tests’ [A] '(1-PropZInt)

x for # of successes, n for sample size, C-level for confidence level as decimal

—> get confidence interval, p̂, and n (again)

"We are C% confident that the interval from [] to [] captures the true [population proportion in context]."

How to get z* with calculator

[2nd] [vars] ‘invNorm’

area is the given C% level but as a decimal

rest ALWAYS μ=0, σ=1, Tail: CENTER

t distribution

when we standardize based on the sample standard deviation, s_x

-t tells us how far x̄ is from the mean μ

_{^{-symmetric w/ 1 peak at 0}}

_{^{-more area in tail (a bit more spread out)}}

degrees of freedom (df)

there is a different t distribution for each sample size

df = n - 1

!!! population distribution (for mean) not normal → statistic has approximately a t_n-1 distribution if the sample size is large enough

incr df (by incr n), shape of t distribution looks closer to standard Normal distribution AND t* closer to z* (roughly approximate each other)

t* → don’t need to know population standard deviation σ (z* does) _{^{(why we use t* usually for pop. mean)}}

t* and z* both critical values (pop mean; pop proportion)

how to get t*

[2nd] [stat] invT

^area is area to the left of the critical value (if C% confidence interval and c is the decimal, then do (1-c)/2)

^df is n-1

t* acts same as z* except it is for constructing confidence intervals for population mean μ

Conditions to check before calculating confidence interval for μ _{^{(population mean)}}

• Random (well-designed random sample or randomized experiment)

• 10% condition (n≤0.1N)

• Normal population distribution OR n≥30 OR no strong skewness/outliers of graphed sample data (even if n<30) _{^{(at least 1 true so can use t interval for μ) (ex: even if graph of sample data is skewed/has outliers, ok to use t interval if large enough sample size)}}

_{^{^DON’T use t procedures if strong skew/outliers and other two possibilities not true
^don’t use t* critical value if not abt pop. mean; not a random sample; n<30 & distrib of sample data is strongly skewed/has outliers}}

standard error of sample mean

use s_x b/c don’t know σ

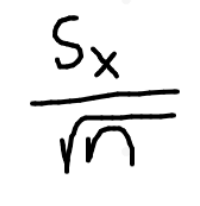
how to get confidence interval of μ

x̄ is statistic

t* is critical value based on C% level

s_x is sample standard deviation

n is sample size

-right side of formula is M.o.E.

—if given data, plug into stat list, then do [stat] ‘calc’ 1-VarStats to get x̄ and s_x

how to find sample size n for pop. mean

use z* (find w/ invNorm) b/c t* relies on knowing sample size n

given M.o.E. (not a proportion (ex: can be 1), plug as is) and SD

round to nearest whole #

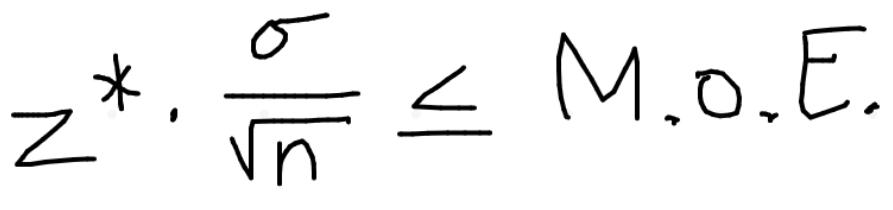
flow chart for margin of error of population mean and when to use what

don’t know σ

• use t* times s_x/√n

know σ

• n≥30 → use z* times σ/√n ← use to find n !

• n<30 → use t* times σ/√n

how to find confidence level w/ pop. mean
_{^{(idk if will use or not)}}

[2nd] [vars] tcdf

lower is -t*, upper is t*, df is n-1

_{^{^only add 1 SE means critical value of t* = 1}}

how to make margin of error/confidence interval narrower

• lower C% confidence level

• larger sample size n