4.2 Null Spaces, Column Spaces, Row Spaces, and Linear Transformations

null of an mxn matrix A, written as NullA is the set of all solutions of the ? equation Ax=0.

homogeneous

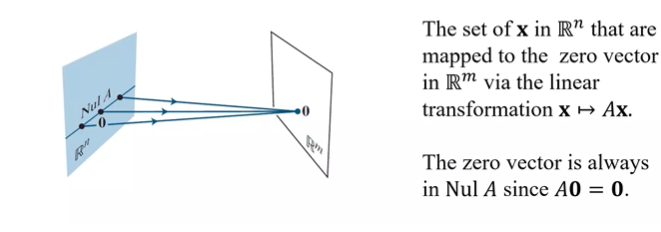
the null space of an mxn matrix A is a ? of Rⁿ

subspace

the set of all solutions to a system Ax=0 is a ? of Rⁿ

subspace

the answer to finding the null space is 

x = free variable [vectors] (it is the general solution

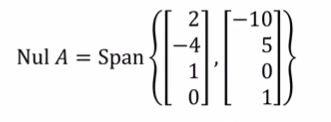
so null A = span of the vectors above ^^

null A = span of the vectors

column space of an mxn matrix A written as Col A, is the set of all ___ ___ of the columns of A

if A = [a1,…an] then ColA = span[a1,…an]

linear combinations

for a column space, the columns of A are in ? and it is a ? of R^m

R^m, subspace

three viewpoints for the column space:

• the set of all vectors Ax for x in Rⁿ

• all vectors b in R^m such that Ax = b is ?

• the range of the linear transformation

consistent

the column space of an mxn matrix A is all of R^m if and only ? has a solution for each b in R^m

Ax=b

the set of all linear combinations of row vectors of A is called the ? of A 

row space

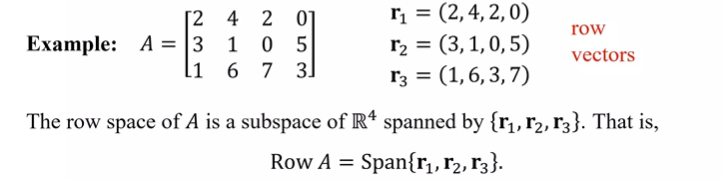
row space of A is a ? of Rⁿ

subspace

rowA = ?

colA^T

contrast between nullA and colA

5. the typical vector v in nullA has the property Av=0. a typical vector v is in col A has the property Ax=v is consistent

6. To show v is in nullA checl Av=0. to show that v is in col A, row generations on [A v] is required

7. NullA = 0 if and only if Ax =0 has onlyhy the trivial solution. ColA = R^m if and only if Ax = b has a solution for every b in R^m

8. NullA = 0 if and only if the transformation x→Ax is one to one. ColA = R^m if and only if the transformation x→Ax is onto R^m

nullA is a subspace of R^m where m is the 

number of entries (columns)

colA is a subspace of R^k where k is the 

number of rows

to check if a vector is in colA (where A is a matrix), you have to reduce Aw in echeclon form and check for ?

consistency

to check if a vector is in nullA (where A is a matrix), you have to compute Aw and see if it is ?

the zero vector

A linear transformation T from a vector space V into a vector space W is a rule that assigns to each vector x in V a unique vector T(x) in W, such that

i. T(u+v) = T(U) + T(v)

ii. T(cu) = cT(u)

kernel (or null space of T/linear trasnformation) is the set of all u in V such that ?

T(u) = 0

the ? of T is the set of vectors in W of the form T(x) for some x in V

range

kernel of T is a ? of V and the range of T is a ? of W

subspace

the subspaces of R² are the:

0 vector, linear single lines through the origin, and R² itself

(T/F) The null space of A is the solution set of the equation Ax=0.

True

(T/F) The column space of an m×n matrix is in ℝm.

True

(T/F) The column space of A is the range of the mapping x↦Ax.

true

(T/F) Nul A is the kernel of the mapping x↦Ax.

true

(T/F) Col A is the set of all vectors that can be written as Ax for some x.

true

(T/F) The set of all solutions of a homogeneous linear differential equation is the kernel of a linear transformation.

true

(T/F) The row space of A is the same as the column space of AT

true