MAT137 Theorems

Chapters 3-5

What is the formal definition of a derivative as a limit?

Let a ∈ R

Let f be a function defined least on an interval centered at a

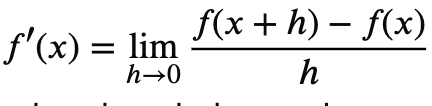
How to write the formal definition of any of the derivative rules?

Let a ∈ R

Let f be a function defined least on an interval centered at a

We define the function “h” h(x) =…

If ______

Then h is differentiable at a, and h’(a) = …

_________________________

Ex. for product rule h(x) = f(x)g(x)

If f and g are differentiable at a

Then h is differentiable at a and h’(a) = f’(a)g(a) + f(a)g’(a)

If a function is differentiable at c, what does this imply?

It is continuous “c”

What are two case examples where a function is continuous but not differentiable?

(1) For corner points (the two sided limits of a derivative do not exist)

(2) When there is a vertical tangent line, and the limit of the derivative approach infinity

What is the if then conditions for finding the derivative of composition of functions.

(e.g. (f∘g)’(x) = f(g(x)) )

Let a ∈ R. Let f, g be functions

IF g is differentiable at a, and f is differentiable at g(a),

THEN f∘g is differentiable at a.

What does a function consist of?

a domain and codomain

Key → Each input may only map to one output

f has an inverse if and only if________.

f is injective (one-to-one) and f is surjective/onto (maps all possible outputs)

When can the inverse of a function be differentiable?

1. f has an inverse

2. f is differentiable

3. for all x in I, f’(x) ≠ 0

When can you say a function has a maximum?

when, there exists a c in I s.t for all x in I, f(c) ≥ f(x)

When can you a function has a local maximum

when, there exists a delta greater than 0, s.t |x-c|<delta implies, f(x) ≤ f(c)

What is the local EVT 

IF

• f has a local extremum at c, and 

• c is an interior point to I 

THEN

• f’(c) = 0 or DNE 

What is the definition of a critical point?

c is a critical point when 

• c is an interior point of the domain f

• f’(c) = 0 or DNE

What is the “Rolle’s Theorem”?

Let a < b. Let f be a function defined on [a, b].

IF

1. f is continuous on [a, b]

2. f is differentiable on (a, b)

3. f(a) = f(b) 

THEN

∃ c ∈ (a, b) s.t. f’(c) = 0

 

How can we predict how many zeroes a function have?

1. calculate at most zeroes from Rolle’s Theorem

2. calculate at least from IVT

What is the mean value theorem?

Let a < b. Let f be a function defined on [a, b].

IF

1. f is continuous on [a, b]

2. f is differentiable on (a, b)

THEN

∃ c ∈ (a, b) s.t. f’(c) = (f(b)-f(a))/(b-a)