unit 7&8 flashcards

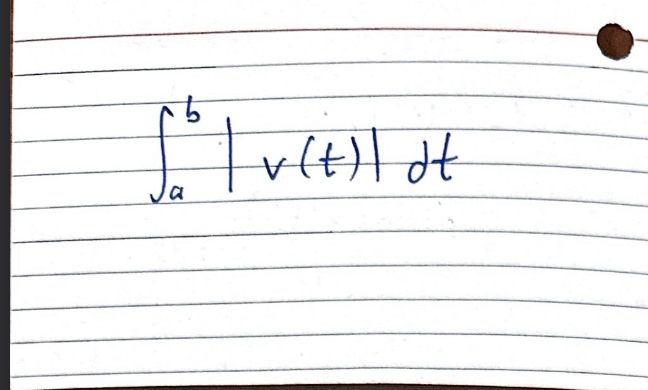
Total distance ( given v(t))

Integral from a to b, absolute value of v(t), dot

Displacement (given v(t))

Integral from a to b, v(t), dt *can be negative

Average value of a function

1/b-a, integral from a to b, f(x) dx…….*f(x) approximately = F(b)-F(a)/b-a

2nd FTC

If F(x) = integral from a to b, f(t) dt, where a is a constant then…..: F’(x)= f(g(x))*g’(x)

Solving a Differential Equation:

• Separate variables

• integrate, don't forget +C!

• use intial condition for c

• check that the equation satisfies the initial condition

Area between 2 curves:

Integral from a to b (points of inflection) Top-Bottom dx

Volume using Disc Method (one function)

• integral from a to v, pi radius to the power of 2 ,dx…. Pi integral from a to b, (f(x)-axis of rotation)²dx

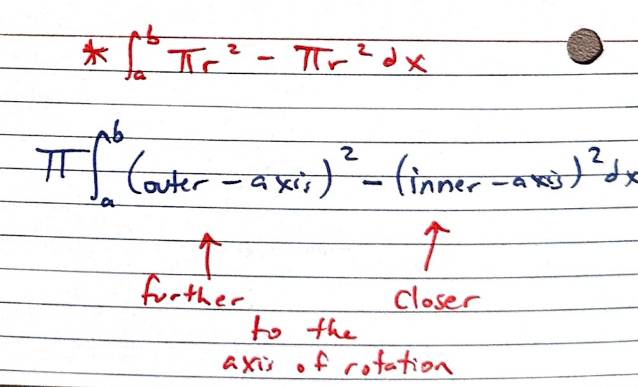
Volume using washer method ( Two functions)

*integral from a to b, pi radius²-pi radius²dx

Pi, integral from a to b, (outer-axis)²-(inner-axis)²dx

Outer is furthest from the axis of rotation

Volumes of Cross sections

Square:

Integral from a to b, [Top-Bottom]²dx

Volumes of Cross sections:

Isosceles

1/2———————-

Volumes of Cross sections:

Equilateral

Square root of 3 / 4—————————

Volumes of Cross sections:

Semi-circle

Pi/8————————