MATS2004 FINAL EXAM

Bonding force and interatomic bonds (influences elastic modulus)

F_A + F_R = 0 in eqm spacing r₀

Attractive force + repulsive force = 0

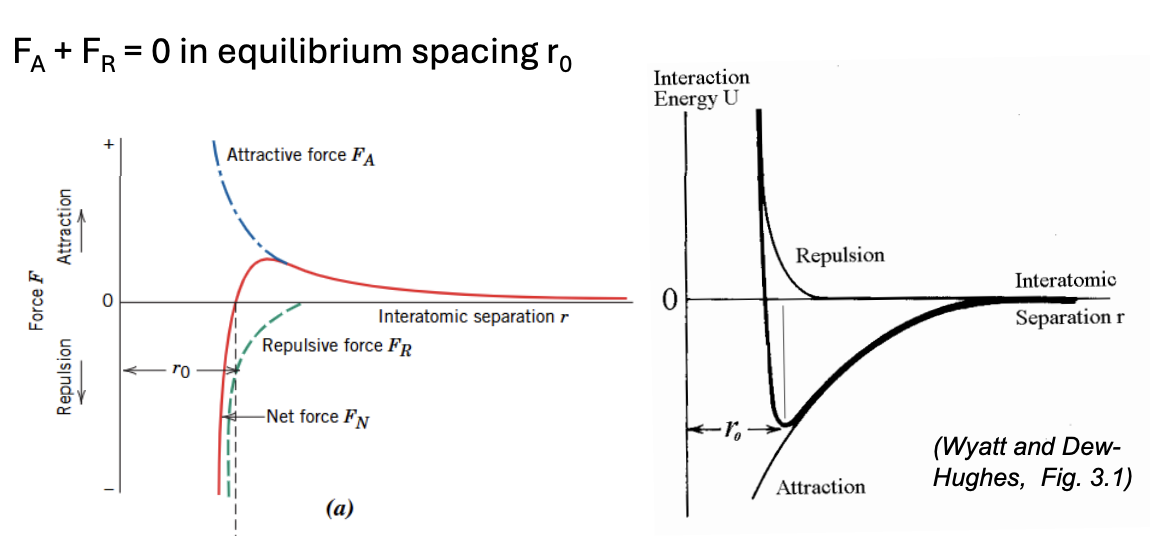
• Atomic binding energy (U) depends on the distance ( r) between atoms

• Min interaction energy is at r₀

How to interpret diagram:

• Where curves intersect the horizontal line = r0 (slope at F = 0)

• Deeper well = more energy

• If the potential energy U(r) is obtained by integrating F(r), which curve represents the deeper energy well?

  • Potential energy = energy to move atoms from eqm distance

  • Deeper energy well as F is larger = larger magnitude of -U(r)

  • From energy conservation:

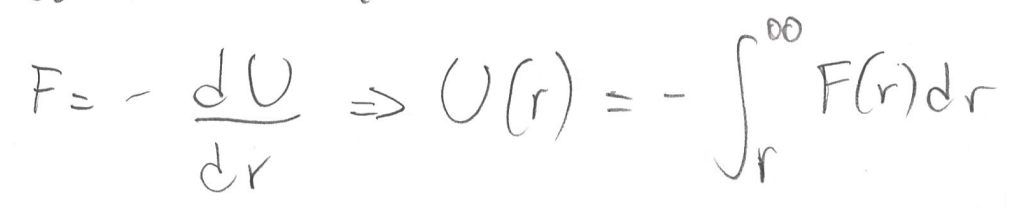
• Consider the formation of a vacancy. Which material would require more energy to remove an atom from the lattice, and why?

  • Deeper well: higher cohesive energy and melting point

Crystal structures and molecular structures in polymers (fundamental to plastic deformation)

Types of interatomic bonds:

• Primary Bonds

  • Ionic

  • Covalent

  • Metallic

• Secondary Bonds

  • Fluctuating induced dipole bonds

  • Polar molecule-induced dipole bonds

  • Permanent dipole bonds

Crystal structure in solid materials:

• Body centred cubic (BCC)

• Face centred cubic (FCC)

• Hexagonal close-packed (HCP)

Molecular structures in polymers:

Defects in crystals (“shortcuts” for deformation)

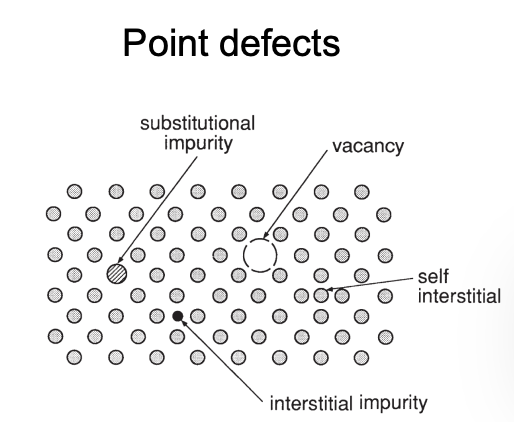
Point Defect:

• Vacancy

• Interstitial

• Substitutional

• Schottky Frenkel

Line Defect: Low-angle boundary in a crystal formed by an array of edge dislocation

• Edge dislocation

• Screw dislocation

Surface Defect:

• Grain boundary

• Twin boundary

Volume Defect:

• Void

• Crack

• Inclusion

• Precipitate

Application of mechanical properties

• Design of engineering components

• Materials selection

• Safety

• Durability

• Manufacturing

• Cost

Determination of mechanical properties

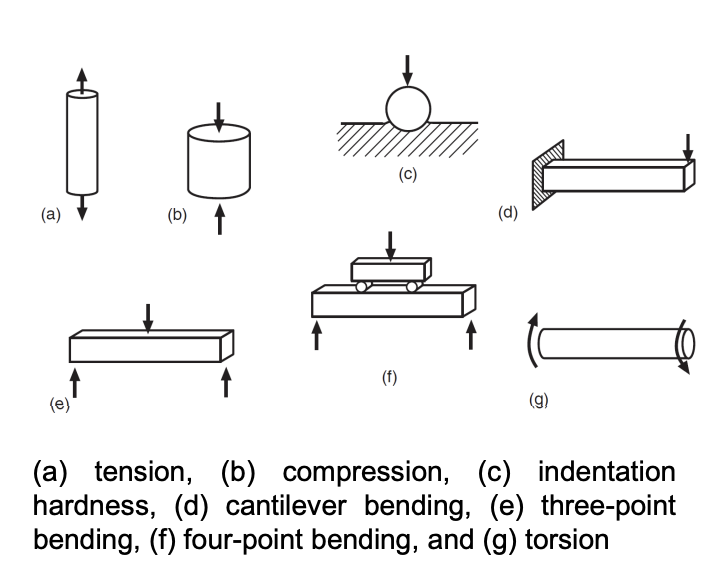
• Tensile test

• compression test

• hardness test

• fatigue test

• airbus A350 wing test (extra)

Time dependent vs independent deformation: Method of mechanical testing

Time-INdependent deformation:

• Elastic

• Plastic

Time dependent deformation:

• Creep = the tendency of a solid material to undergo slow deformation while subject to persistent mechanical stresses

Stress, Normal stress, Shear stress

Stress = intensity of force (P) at a point in body under load

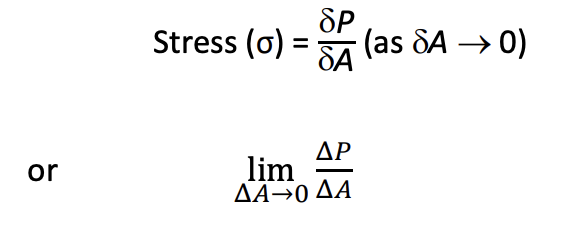
Stress components:

• Any stress state may be resolved into NORMAL stress and SHEAR stress or into 3 PRINCIPAL stresses

Normal stress (σ) (plane x) = force per unit acting normal to the surface.

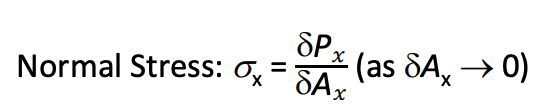
Shear stress (τ) (plane x, direction y) = force per unit area acting parallel to surface.

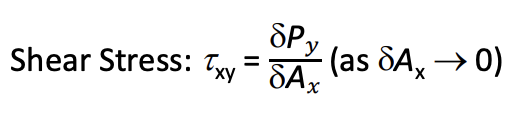
average/conventional stress, true stress and nominal stress

For a uniaxial stress with uniform stress distribution across a section, conventional stress is average intensity of force over the section:

Strain, nominal strain vs shear strain

Poisson effect

A body upon being pulled in uniaxial tension, tends to contract laterally as it extends.

Poisson ratio = measures this effect. Negative ratio of transverse strain (strain perpendicular to the force) to axial strain (strain in the direction of the force).

v of emtals ~ 0.3.

Mechanical Testing 1: Tension test

Load vs extension

Nominal stress vs nominal strain (engineering stress-strin curve)

True stress vs true strain curve (flow curve)

Material properties:

• Elastiic modulus, poisson ratio

• strength: proportional limit, yield strength, UTS, engineering fracture strength

• Ductility: % elongation, reduction in area

• Energy capacity: tensile toughness

• Strain hardening

Mechanical Testing 2: Compression test

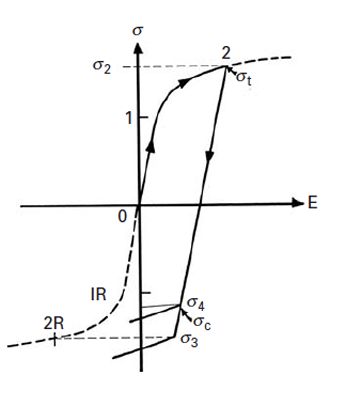
Barrelling = a nonuniform plastic deformation resulting from friction between the specimen and the platen. (playdough)

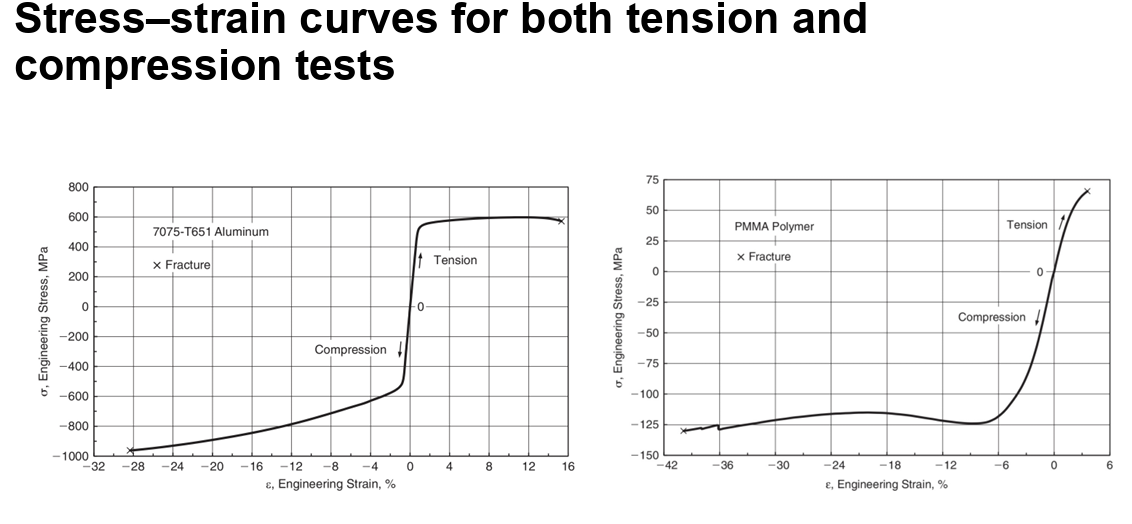
Bauschinger effect

A material that is pulled in tension, shows a reduction in compressive strength

Hardness test - Brinell

Plastic deformation under a brinell hardness indenter.

A steel sphere is pressed against a metal surface for a specified period of time and the surface of the indentation is measures. The load (in kgf) is divided by the area (mm2) of the curved surface to give HB.

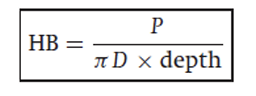
Hardness Test - rockwell

Indentation made by application of the minor and major load on a diamond Brale indenter.

Hardness test - rockwell vs brinell vs vickers

The Rockwell test is a rapid, widely used method measuring indentation depth for various materials, suitable for quick, automated testing, while Brinell and Vickers are optical methods measuring the surface area of a permanent indentation made by a sphere (Brinell) or a diamond pyramid (Vickers). Brinell is ideal for soft, coarse-grained materials like cast iron, whereas Vickers offers precision for very hard, thin, or heterogeneous materials and microhardness testing

The Brinell test is better for large, soft, or inhomogeneous materials like cast iron, as it uses a large indenter and measures the indentation's diameter to provide an average hardness value. In contrast, the Rockwell test is quicker and more suitable for hard materials and homogeneous structures, as it uses a smaller indenter (ball or cone) and measures the depth of the indentation for a direct readout, allowing for high automation and accuracy. 

Hardness test - vickers hardness indentation

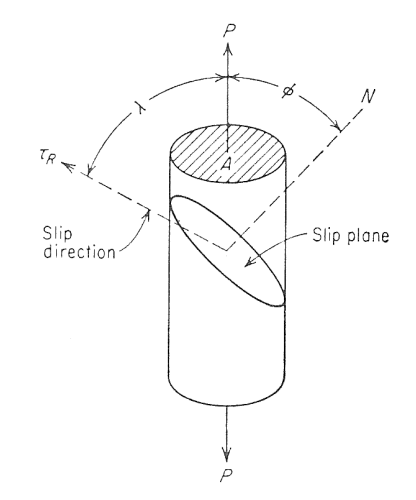
Torsion test:

A round bar in torsion and the resulting state of pure shear stress and strain. The equivalent normal stresses and strains for a 45° rotation of the coordinate axes are also shown

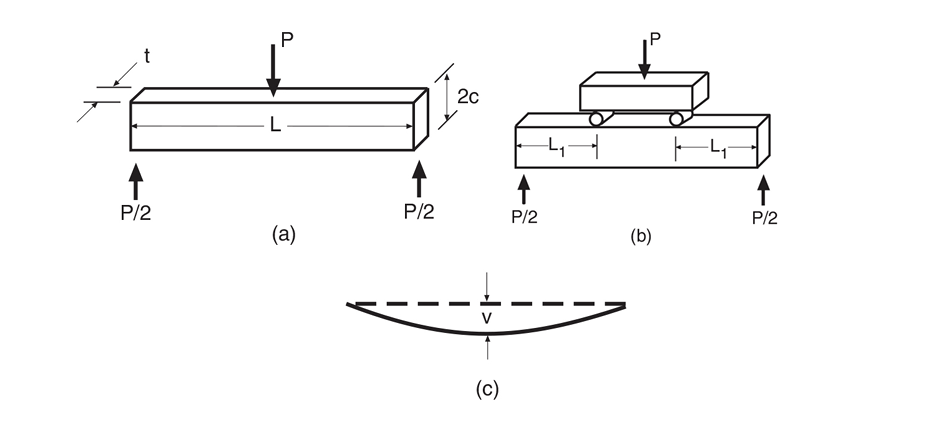
Bending test:

Loading configuration for (a) three-point bending and (b) four-point bending. The deflection of the centerline of either beam is similar to (c)