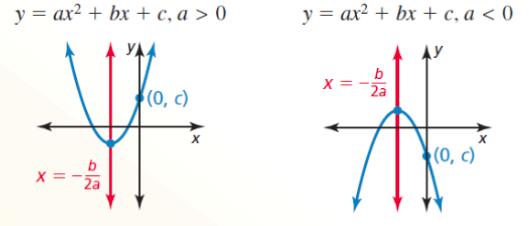Chapter 2: Quadratic Functions

• Lesson 1: Transformations of Quadratic Functions
    * Quadratic Functions
      * A quadratic function is a function that can be written in the form f(x) = a(x - h)2 + k, where a ≠ 0
      * The U-shaped graph of a quadratic function is called a parabola
    * Translations
      * Horizontal Translation
        * f(x) = x2
        * f(x - h) = (x - h)2
        *
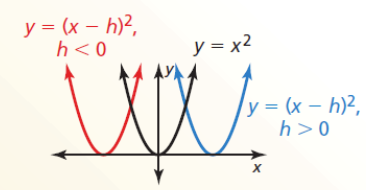
        * Shifts left when h < 0       * Shifts right when h > 0
      * Vertical Translation
        * f(x) = x2
        * f(x) + k = x2 + k
        *
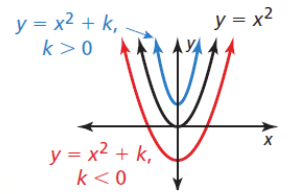
        * Shifts down when k < 0       * Shifts up when k > 0
    * Reflections
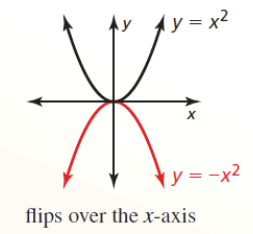
      * Reflection in the x-axis
        * f(x) = x2
        * -f(x) = -(x2) = -x2
        *
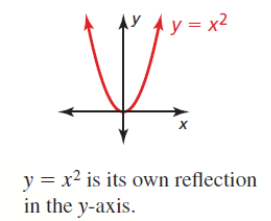
      * Reflection in the y-axis
        * f(x) = x2
        * f(-x) = (-x)2 = x2
        *
    * Stretches and Shrinks
      * Horizontal Stretches and Shrinks
        * f(x) = x2
        * f(ax) = (ax)2
        *
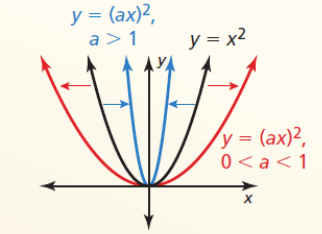
        * Horizontal stretch (away from y-axis) when 0 < a < 1       * Horizontal shrink (towards y-axis) when a > 1
      * Vertical Stretches and Shrinks
        * f(x) = x2
        * a * f(x) = ax2
        *
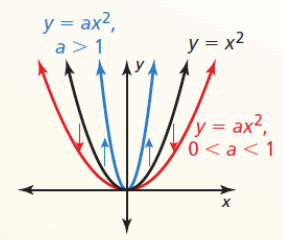
        * Vertical stretch (away from x-axis) when a > 1
        * Vertical shrink (towards x-axis) when 0 < a < 1
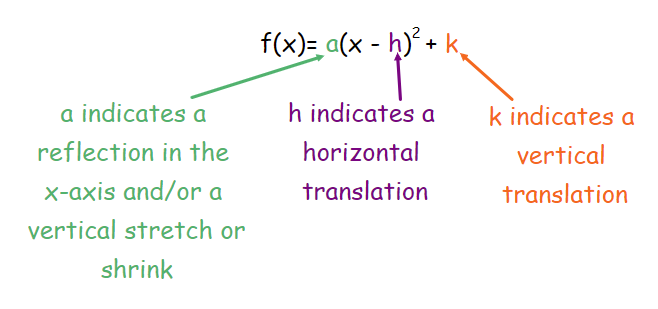
    * Vertex Form
      * The lowest part on a parabola that opens up or the highest point on a parabola that opens down is called the vertex
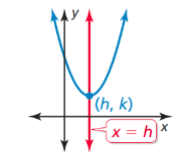
      * The vertex form of a quadratic function is f(x) = a(x - h)2 + k, where a ≠ 0 and the vertex is (h, k)
      *
• Lesson 2: Characteristics of Quadratic Functions
    * Quadratic Function Forms
      * Axis of Symmetry - a line that divides a parabola into mirror images and passes through the vertex; the axis of symmetry is the vertical line x = h or x = -b/2a
      *
      * Standard Form - a quadratic function written in the form f(x) = ax2 + bx + c
      * Intercept Form - a quadratic function in the form f(x) = a(x - p)(x - q)
    * Properties of the Standard Form
      *
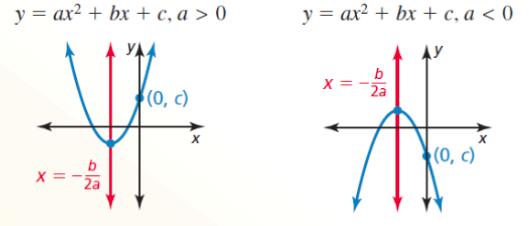
      * The parabola opens up when a > 0 and opens down when a < 0     * The graph is narrower than the graph of f(x) = x2 when |a| > 1 and wider when |a| < 1     * The axis of symmetry is x = -b/2a and the vertex is (-b/2a, f(-b/2a))     * The y-intercept is c; the point (0, c) is on the parabola   * Minimum and Maximum Values     * For the quadratic function f(x) = ax2 + bx + c, the y-coordinate of the vertex is the minimum value of the function when a > 0 and the maximum value when a < 0     *
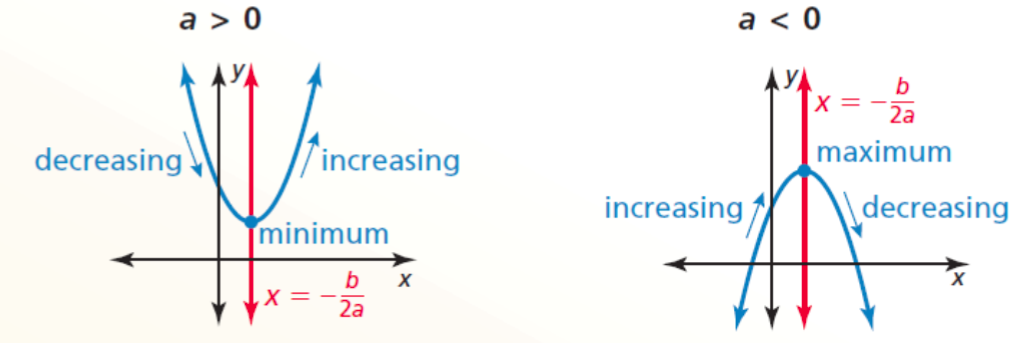
      * a > 0
        * Minimum value: f(-b/2a)
        * Domain: all real numbers
        * Range: y ≥ f(-b/2a)
        * Decreasing to the left of x = -b/2a
        * Increasing to the right of x = -b/2a
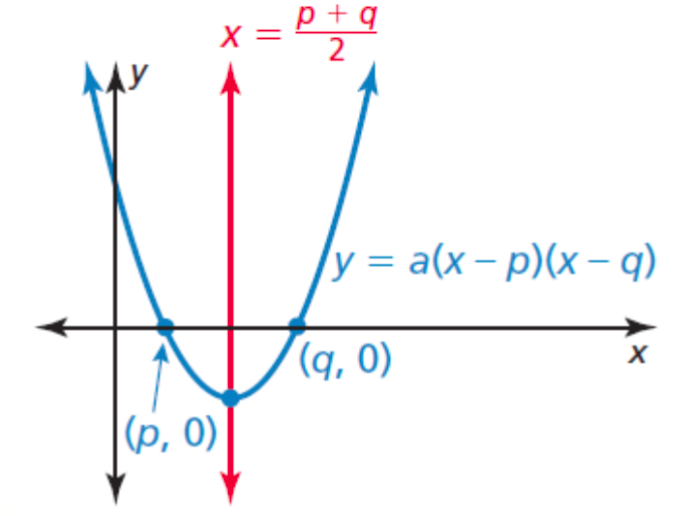
      * a < 0       * Maximum value: f(-b/2a)       * Domain: all real numbers       * Range: y ≤ f(-b/2a)       * Increasing to the left of x = -b/2a       * Decreasing to the right of x = -b/2a   * Properties of the Intercept Form     * Because f(p) = 0 and f(q) = 0, p and q are the x-intercepts of the graph of the function     * The axis of symmetry is halfway between (p, 0) and (q, 0); x = (p + q)/2     * The parabola opens up when a > 0 and opens down when a < 0     *
• Lesson 3: Modeling with Quadratic Equations
    * Writing Quadratic Equations
      * Given a point and the vertex (h, k), use vertex form: y = a(x - h)2 + k
      * Given a point and x-intercepts p and q, use intercept form y = a(x - p)(x - q)
      * Given three points, write and solve a system of three equations in three variables

\