PSYC 210 - Introduction to Statistical Analysis

Flashcards made regarding the main concepts!

Sampling Distributions

Plotting a statistic based on repeated sampling in a population.

What are the population symbols?

Mu (population mean)

Sigma (population standard deviation)

N (population size)

What are the sample symbols?

X bar (sample mean)

s (sample standard deviation)

n (sample size)

Mean of the means (grand mean) from sampling distribution is..

An unbiased estimate of the population parameter

Sampling Distribution of the Mean

Mean of all samples repeatedly collected from the population and plotted as a distribution

AKA an estimation of the population mean

Standard Error (𝜎𝑥̄)

how wrong your sample mean might be on average from the true population mean.

A larger SE means your sample mean could be further from the true mean, so there is more uncertainty.

Standard score

AKA Z-score

Standard Deviation

how far, on average, each data point is from the mean.

Effect Size

Even if your result is statistically significant, the effect may be tiny. The effect size tells us about whether the difference or relationship is meaningful in REAL LIFE.

Variance

The average amount of spread of data from the mean in SQUARED UNITS (s²)

Sum of Squares

Sum of all squared standard deviations from the mean, used to find variance and standard deviation (SD).

Degrees of Freedom

How many numbers are free to vary

Higher df: more sample size, better estimates of SD and variance

Confidence Interval

range of values where the true population mean or the true difference between means lie

• 95% CI → if you repeated your experiment many times, 95% of the calculated intervals would contain the true mean.

• Wider CI → more uncertainty → larger SE or smaller sample size

• Narrower CI → more precision → smaller SE or larger sample size

Type I Error

u think ur treatment has an effect but it doesnt

Type II Error

treatment has an effect but u conclude that it doesnt

If we have population mean and standard deviation we can use…

a Z-test

If we don’t have population standard deviation, we can use…

one sample t-test

If we don’t have population sample and standard deviation, we can use…

two samples independent t-test

hypothesis for dependent measures t-test

mu dbar = 0

mu dbar does not equal 0

what two measures of variance does anova compare

variance of the group means around the grand mean (between) vs variance of individual scores around their group mean (within)

between-group variance

how spread apart each group’s mean score is

(the difference between the classroom averages)

within-group variance

how spread apart each individual score in the group is

(the difference between students in the classroom)

what is mean squares between (MSB)

variance between group means, how far apart the group means are from each other

what is mean squares within (error)

MSwithin measures the average variance inside each group.

It represents the “error” or noise—how much individual scores fluctuate around their own group mean.

what does it mean if MSB is low

groups are similar = supports the null hypothesis

what does it mean if MSB is high

groups aren’t similar = supports the alternative hypothesis

how to calculate df within

n-k

Fratio formula

MSb/MSw

how to calculate df between

k-1

Steps for solving a One way ANOVA?

1) define hypothesis (null: mu1 = mu2 = mu3, alt. hypothesis: not h0)

2) solve for between-group sum of squares
(SSbetween = Sigma (sample size) [xbar - xGM]²)

3) solve for within-group sum of squares by adding together all variance

4) find the degrees of freedom for within and between group
5) solve for mean of squares

MSbetween = ssbetween/df between

MSwithin = sswithin/df within

6) solve for f-ratio: MSbetween/MSwithin

ANOVA IN BRIEF (for reference)

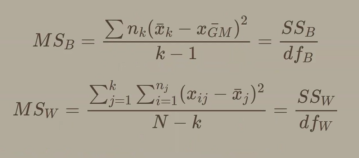
r²

how much of the variation in one variable can be explained by the other

Spearman correlation coefficient

• Measures the relationship between ranks (ordered data).

• Works when data isn’t normally distributed or when you only care about order, not exact values.

➢Point-biserial correlation coefficient

to measure one variable that is continuous (on an interval or ratio scale of measurement) and a second variable that is dichotomous (on a nominal scale of measurement)

Phi correlation coefficient

to measure two dichotomous variables.

Univariate outlier

Weird on either predictor or response variable

Regression outlier

Weird for the regression model (large residual)

Influence

Weird on predictor variable and weird on response variable and has a large residual