Lecture 3 - Entropy

Expression of first law of thermodynamics

• Law = conservation of energy

• Related to work ΔW and heat ΔQ exchanged with surroundings as ΔU = ΔW + ΔQ.

ΔU for ideal gas

ΔU = n* C_v*ΔT

ΔU for different processes

• ΔU = Internal energy

• For isothermal processes: ΔT = 0 → Internal energy = constant ΔU = 0 → ΔQ = -ΔW

• For isochoric processes → no work → ΔW = 0 → ΔU = ΔQ

• For adiabatic processes → no heat flow → ΔQ = 0 → ΔU = ΔW

Adiabatic processes

adiabatic process: ∆𝑄 = 0

• System is adiabatically isolated (perfect insulation)

• In real life → insulation ≠ perfect

• Very fast processes → limited heat exchange → assume adiabatic → ∆𝑈 = ∆𝑊

• Adiabatic cooling: decrease pressure → system expands → system performs work on surroundings (∆𝑊 < 0) → internal energy decreases → temperature decreases
  ∆𝑈 = n𝐶𝑣∆𝑇

Example adiabatic process (can of coke)

Opening a can of coke:

• Can is openend, CO₂ starts to expand.

• Internal energy of the CO₂ goes down, therefore temperature also goes down

• Surrounding becomes cool, in surrounding we have moisture (water vapor)

• Therefore release of water vapor from can happens

• Would not happen in desert because there is no water vapor in the air.

Example of adiabatic process (Fire exthinguisher)

• Fire extinguishers also are filled with CO₂

• The cans also have higher pressure

• When using, liquid expands very fast, leading to very fast cooling

• CO₂ turns into solid, powder like CO₂

Macrostate

Number of balls * level

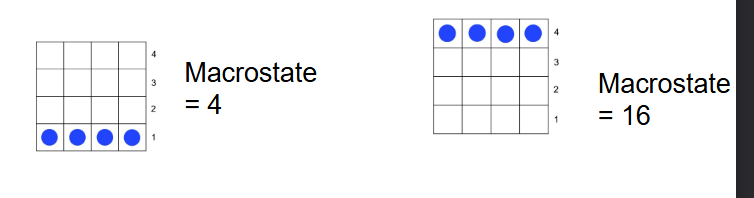
When is entropy highest?

• At macrostate 10

• Highest when system arranged in most probable way

How to calculate entropy?

Shape of polymer and entropy

• Pull on each end of polymer chain

  • Enough force → completely extend → less probable configuration → reduction in entropy

• Release tension

  • Back to more probable configuration → increase in entropy → entropic elasticity

  • Not necessarily exactly same configuration as start

Enthalpy

• Concept of enthalpy H = U + pV

• H is a state variable (does not depend on the path)

• ΔH = ΔQ

• Heat Q is not a state variable

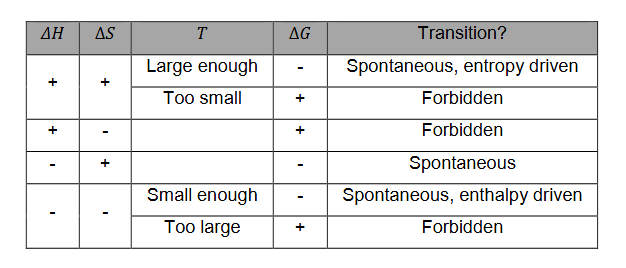
Gibbs free energy

• System will always strive to have a minimal value for G at fixed T and p

• Gibbs free energy is minimized when enthalpy is minimized and entropy is maximized.

What happens when G is 0?

We have thermodynamic equilibrium

• When we have a change in the system, G should decrease, otherwise the change is forbidden

• G<0

Relation H, S, T and G

Melting of ice as an example of Gibbs free energy

• Heat is added to induce phase transition → ΔH > 0

• Water has a higher degree of disorder than ice ΔS > 0 → -TΔS < 0

• At melting temperature or higher T: TΔS > ΔH → ΔG < 0 and the transition happens.

Chemical potential

• A chemical potential μ to each phase

• μ^solid, μ^liquid, μ^gas

• When in the liquid phase for example μ^liquid < μ^solid, μ^gas

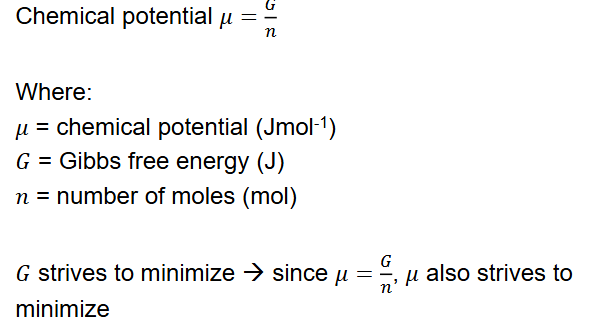
What is the most stable phase?

What are G and μ when you are on the border of a line in the phase diagram?

Because G is equal so will μ be

• So at the triple point μ^solid = μ^liquid = μ^gas

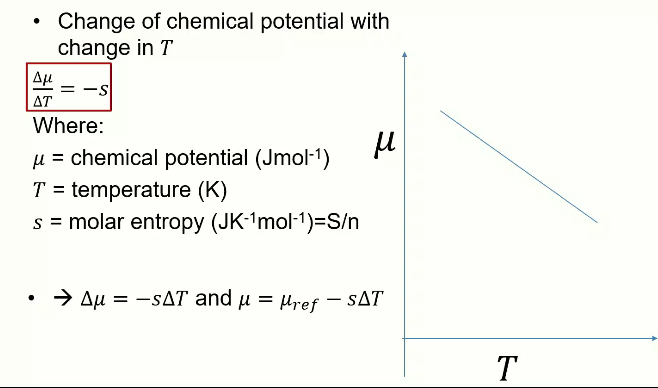
Relation between Δμ, ΔT and -S

• When entropy is higher, the slope is also greater.

• Using this formula you can predict the entropy for each state and model it.

• Again when these phase lines intersect μ increases.

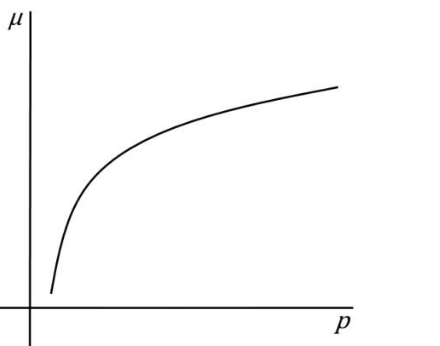
Relation between Δμ, Δp and v

• Can also be used to make a line as a function of pressure

How to find the chemical potential of an ideal gas

Chemical potential = RT*ln(p2/p1)

In the case of a mixed gas:

Chemical potential = μ_ref + RTlnx_gas

What causes a change in W (in first law of thermodynamics)

• Any change of space

• Compression of gas: -W

• Expansion of gas: +W

• Change in W will be positive

Relation temperature and internal energy

Has a direct link: higher t = higher delta U

Graph of ideal gas molar volume against pressure

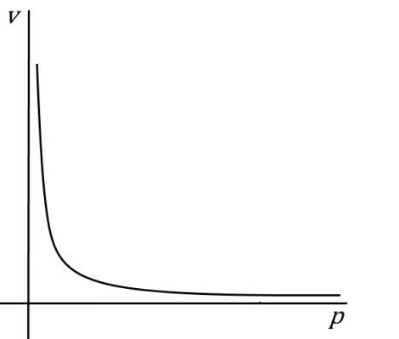
Graph of ideal gas chemical potential against pressure