Algebra 2 Rational Functions

what is a undefined or restricted value?

a value that makes the denominator = 0

How do we find restricted values?

Set the denominator equal to 0 and solve

Find the restricted value:

3x/x+5

x = -5

Steps to simplify rationals

• Factor both the numerator & denominator

• cancel like factors from the numerator & denominator

• write simplified answer

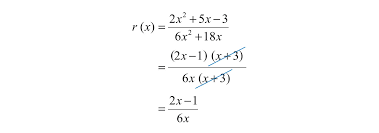
Simplify.

x² + 3x

x² + 5x

x + 3 / x + 5

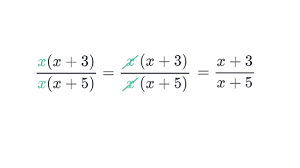
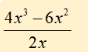
Simplify.

x(2x-3)

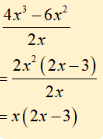
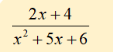
Simplify.

2 / x + 3

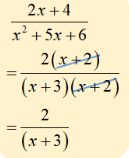
Steps to multiply rationals

• DO NOT MULTIPLY. I REPEAT, DO. NOT. MULTIPLY

• Factor numerators & denominators

• cancel like factors and write remaining expression

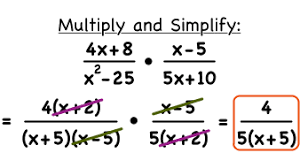
Steps to divide rationals

• DO NOT DIVIDE.

• multiply by the reciprocal of the second rational expression

• Follow process for multiplying

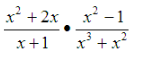
Multiply.

(x + 2) (x - 1) / x(x + 1)

Divide.

(x - 8) ( x - 5) / (x + 7)²

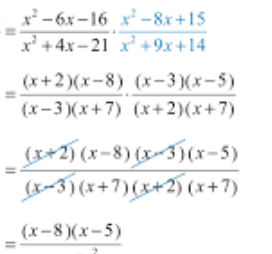
Steps to add rationals

• ALWAYS make sure the denominators are the same

• Then, add the numerators by combining like terms.

Steps to subtract rationals

• Make sure the denominators are the same

• Combine like terms, and don’t forget to distribute the negative sign if necessary!

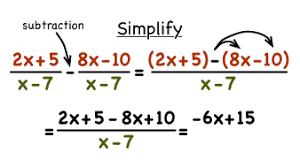
To find common denominators…

• Only use each factor once

• factor each denominator individually & find the LCD

• multiply them together to get a combined denominator

• multiply the numerator by the respective denominator (see example)

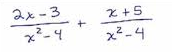
Add.

3x + 2 / (x + 2)(x - 2)

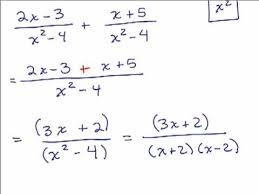
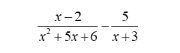
Subtract.

-4 / x + 2

Steps to solving rational equations

• find common denominators (multiply rationals by a factor to make them all have the same denominator)

• cross out the denominators and solve the remaining equation

• check for extraneous (restricted values) solutions

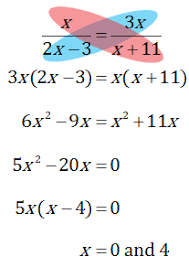
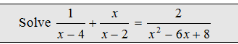
Solve.

x = -1

4 is extraneous.

vertical asymptote

set denominator = 0 and solve.

• written as x = #

domain

All real numbers except the vertical asymptote you found.

horizontal asymptote

Use the degrees of the numerator & denominator

• equal degrees : coefficients of leading terms

• numerator < < denominator : HA = 0

• numerator > > denominator : NO HA

Written as y = #

range

All real numbers except the horizontal asymtote you found. If no HA, then its all reals.

x intercept

set numerator = 0 and solve

y intercept

plug in zero for all x-values

holes

if you can cancel a factor from the numerator & denominator, then there is a hole at that x value.

Find the characteristics:

x - 2 / x + 2

• factored

• VA: x = -2

• Domain: R: x cant be -2

• HA: y = 1

• Range: R: x cant be 1

• X-INT: (2,0)

• Y-INT: (0,-1)