Math 152 Midterm 3 Review Sheet (Fall 2025)

Practice flashcards created for the Math 152 Midterm 3 review sheet to assist studying important concepts and formulas.

The series in geometric series converges absolutely to __ if |r| < 1.

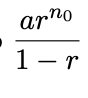
The N-th Term Test states that if __, then the series diverges.

limn→∞ an ≠ 0

The Integral Test requires that f(x) is positive, continuous, and __ for x > A.

decreasing

The p-series converges if __ and diverges otherwise.

p > 1

If an ≤ bn for all n > N and the series ∑bn converges, then __ according to the Direct Comparison Test.

∑an converges

In the Limit Comparison Test, if L is in the interval (0, ∞), then ∑an and ∑bn either both __ or both diverge.

converge

The Absolute Convergence Test states that if ∑|an| converges, then ∑an __.

converges

The Ratio Test indicates that if ρ < 1, then the series converges __.

absolutely

The Alternating Series Test requires that un are eventually __ and limn→∞ un = 0.

non-increasing

The Maclaurin series for e^x is __.

∑(x^n / n!)

The Taylor series generated by f at x = a is given by __.

T(x) = ∑(f(k)(a) / k!)(x - a)^k

The Taylor polynomial of order n generated by f at x = a is __.

Pn(x) = f(a) + f′(a)(x − a) + … + f(n)(a) / n!(x − a)^n