week 3 Student T-tests and Effect sizes

one sample t-test

compare a single mean to a fixed number or ‘gold standard’

e.g. weight indicated on a can of soft drink

independent samples two sample t-test

compare two population means based on independent (unpaired) samples from the two populations or groups

e.g. do males react differently to certain drugs than females

paired t-test

compare two means based on samples that are paired/repeated measures in some way- before and after

e.g. does a hopping intervention improve bone mineral density

hypotheses for one sample t test

null- the mean height of 9 year old boys is not different to the average height on 9 year olds

alternative-the mean height is different to the reference population

parametric assumptions

continuous data

normally distributed

same variance

checking assumptions SPSS

statistic is non significant (p value>0.05)=normal distribution using Shapiro-WIlkes

two tailed

null: the population mean is equal to the hypothesised value

alternative: the population mean is not equal to the hypothesised value

one sided t-test

null: the population mean is equal to the hypothesised mean
alternative: the population mean is greater than/less than the hypothesised value

SPSS output to test hypothesis

if alpha=0.05, the p-value has to be less to reject the null hypothesis

if alpha=0.01, it is necessary for the p-value to be less than 0.01 to reject the null hypothesis

SPSS output one sample t test

if 95% confidence interval overlaps 0, we cannot be sure there is a real difference

reporting results of a one sample t-test

method: what test was performed to test what hypothesis

results: test of normality confirms what (w and p). The mean difference (mean and SD) was/not significantly different the the general population of (df, alpha level, tails)

two sample t-test assumputions

• continuous ratio/interval

• randomly selected

• normality

• equality of variance

hypotheses

null: the population means of the two groups are the same

checking equality of variances

Levene’s test of equality of variances should be non-significant

reporting an independent samples t test

method: type of test an hypothesis

results: checking assumptions, mean difference indicates (non) significiant (mean, SD, t, p, tails) conclusion

one tailed test for independent samples t test

read the significance value for one sided p from SPSS output

independent t test cautions

dont use for comparing paired subjects or comparing to a known value

preplan directional one tailed t-tests with strong evidence

small sample sizes make normality difficult to assess

performing multiple t-tests causes loss of control of the experiment-wise significance level

paired t test assumption

continuous ratio/interval data

normality of the difference

paired t test hypothesis

null: the population mean of the differences is 0

directional hypothesis

set an alpha level 0.01

reporting results paired t-test

method: test and hypothesis

results: shapiro wilkes, test indicates (non) significance-report Mean, M, SD for before and after, t(df) and p, tails to show what conclusion

samples sizes

• As the size of a sample increases, the standard error becomes smaller, and the p-value tends todecrease. ​

• Occasionally a “statistically significant” result suggests that a large sample size was used.

reporting effect sizes

• Reflect the magnitude of effects obtained in experiments

• Applying a test of significance only and stating the p-value may only provide information about the presence or absence of a difference.​

• allow the results from different sources and authors to be properly compared.

• can be used to calculate the power of a statistical test (power statistics),which in turn allows the researcher to determine the sample size needed for the study.​

• estimates obtained in pilot studies where the sample size is often small may be an indicator of future expectations of research results.

d effect size

Assesses the Differences between groups​

• Groups can be compared on dichotomous or continuous variables. Where we compare groups on dichotomous variables(e.g., treated versus untreated),comparisons may be based on the probabilities of group members being classified into one of the two categories.

r effect size

Measures the Strength of a relationship/association​

• The effect sizes covers various measures of association involving two (or more)variables. Many of these measures are variations on the correlation coefficient

strengths of d defintions-cohen 1969

Small effect = 0.2 ​

(0.2 <0.5)​

Medium effect = 0.5 ​

(≥ 0.50 <0.80)​

Large effect > 0.8 ​

(≥ 0.80)

cohen 1988 strength of r

Weak/Small sizes correlation / effect r = 0.10 ​

(0.10 <0.30)​

Medium sized correlation / effect r = 0.30 ​

(≥ 0.30 <0.50)​

Large sized correlation / effect r = 0.50 ​

(≥ 0.50)

calculating parametric effect size - d statistic

• d = Cohen’s d index of effect size​

• a = Mean of Drug A​

• b = Mean of Drug B​

• SDp = Pooled Standard Deviation

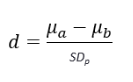
SD pooled

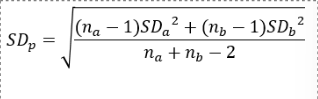
reporting effect size

effect size based on cohen (year) benchmark suggests a small/medium/large effect

paired t test effect size

cohens r

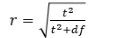
SPSS effect sizes

do not request effect sizes in SPSS unless it uses pooled standard deviation (independent samples)