Chapter 10 Vocab

Circumference of a Circle

C=2πr or C=πd

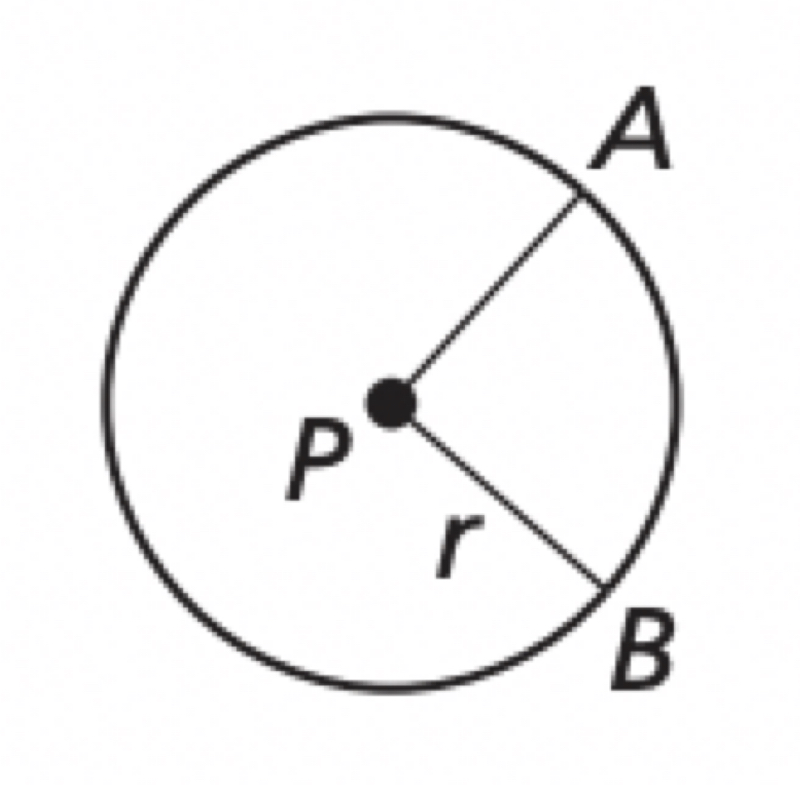
Arc Length

In a circle, the ratio of the length of a given arc to the circumference is equal to the ratio of the measure of the arc to 360°. Arc length of arc AB / 2πr = m arc AB / 360

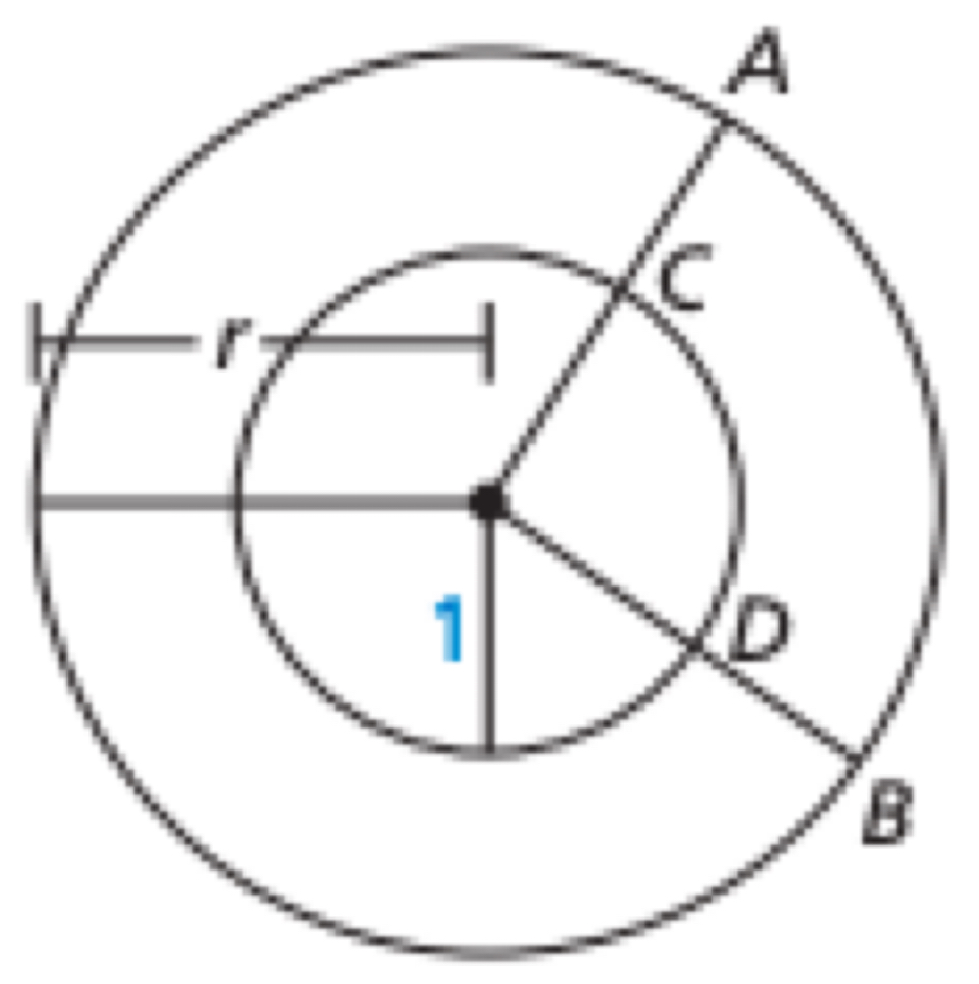
Radian Measure

The constant of proportionality, m arc CD / 360 • 2π, is defined to be the _____ ______ of the central angle associated with the arc

Converting Degrees to Radians

Multiply degree measure by π radians / 180°

Converting Radians to Degrees

Multiply radian measure by 180° / π radians

Area of a Circle

πr²

Population Density

How many people live in a given area. Number of people / area of land

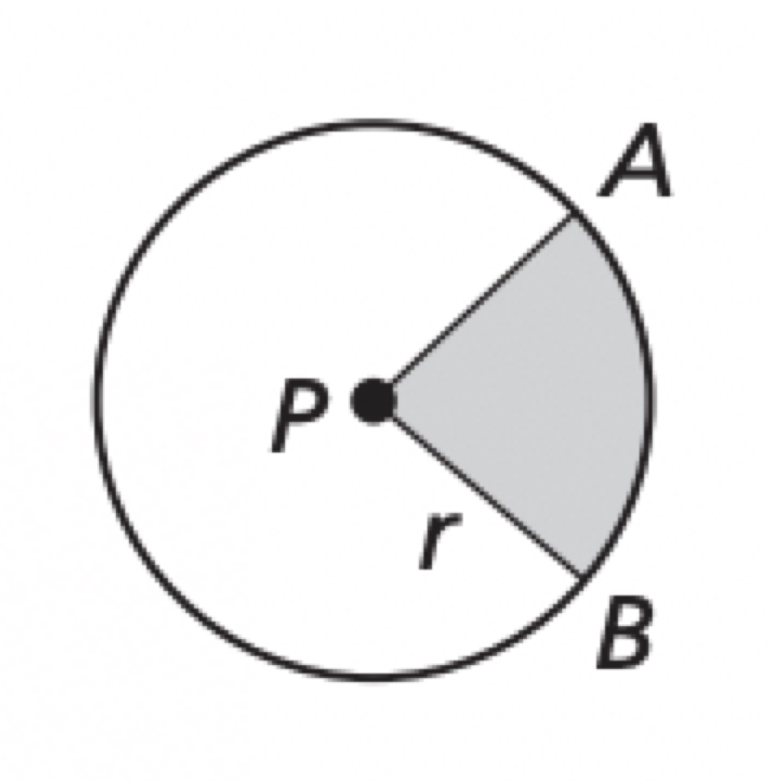
Sector of a Circle

The region bounded by two radii of the circle and their intercepted arc. In the diagram below, sector APB is bounded by AP, BP, and arc AB

Area of a Sector

The ratio of the area of a sector of a circle to the area of the whole circle (πr^2) is equal to the ratio of the measure of the intercepted arc to 360°. Area of sector APB / πr^2 = m arc AB / 360, or Area of sector APB = m arc AB / 360 • πr²

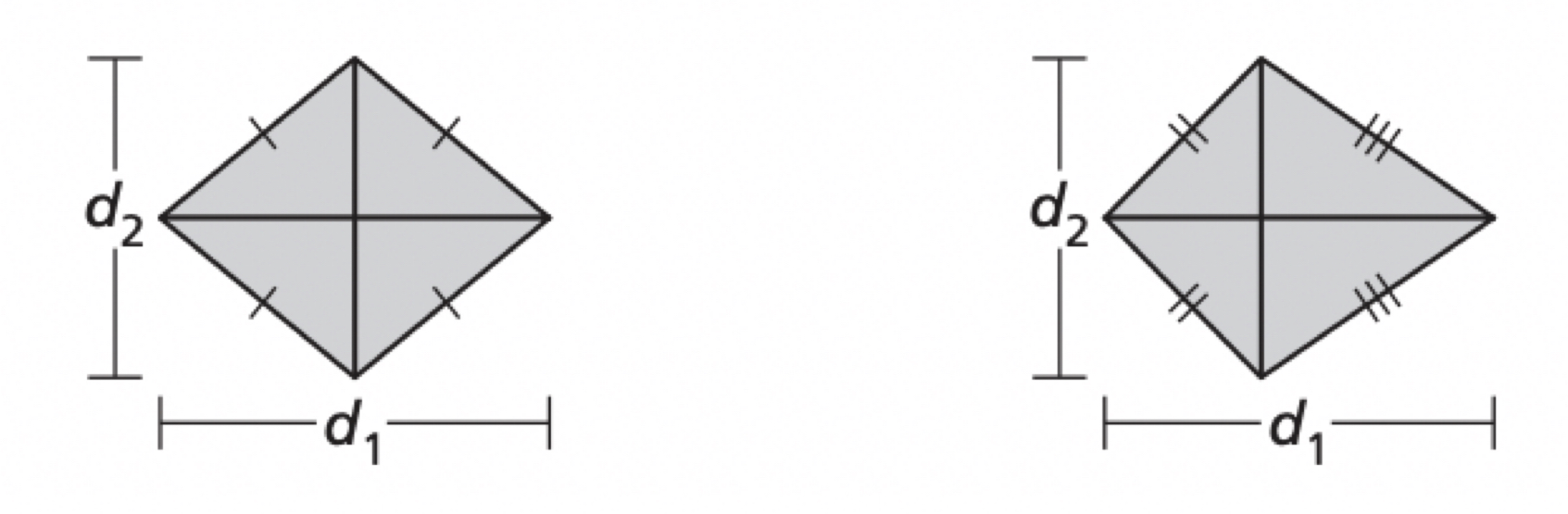
Area of a Rhombus or Kite

The area of a rhombus or kite with diagonals d1 and d2 is ½ • d1 • d2

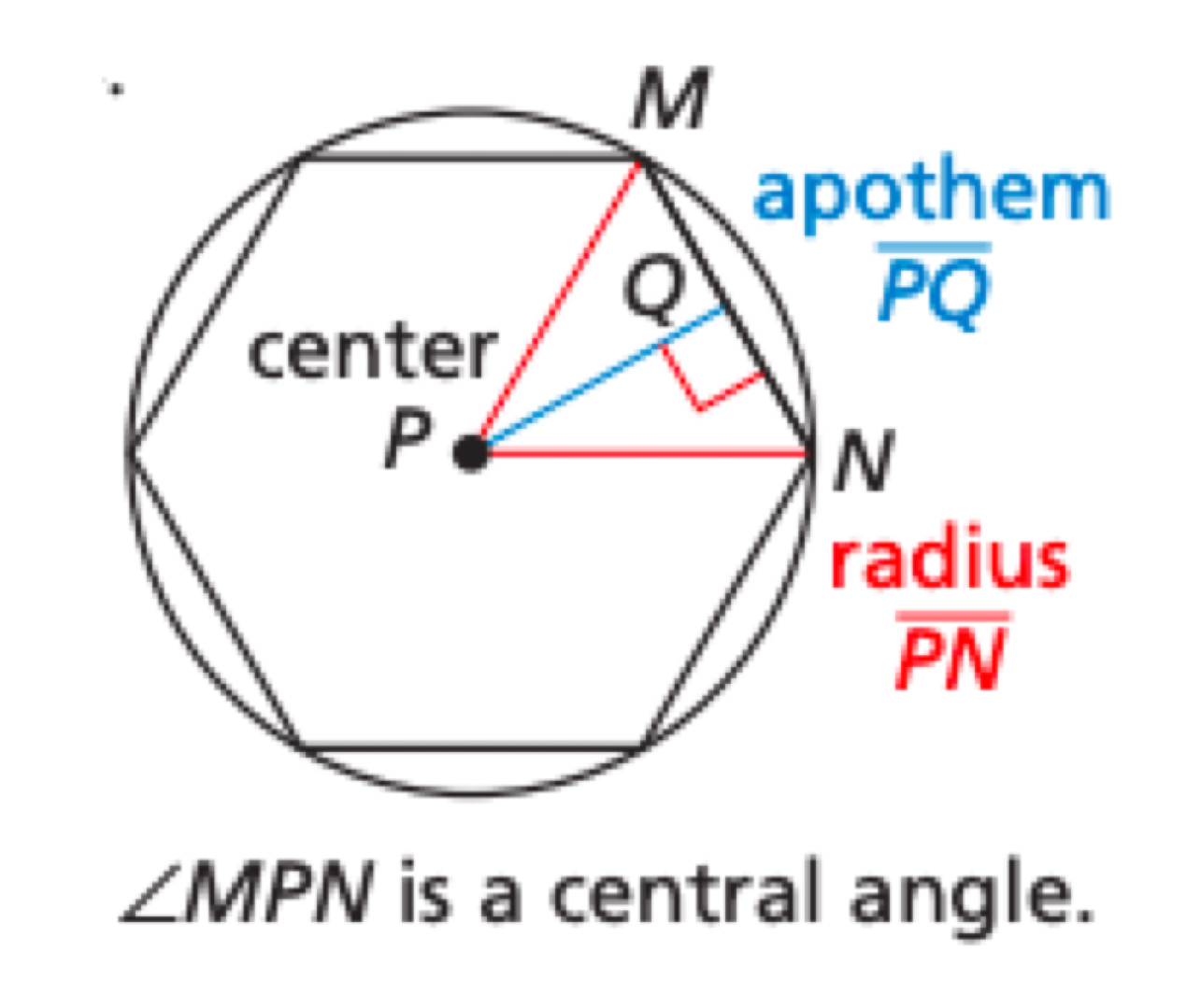
Center and Radius of a Regular Polygon

The center and radius of its circumscribed circle

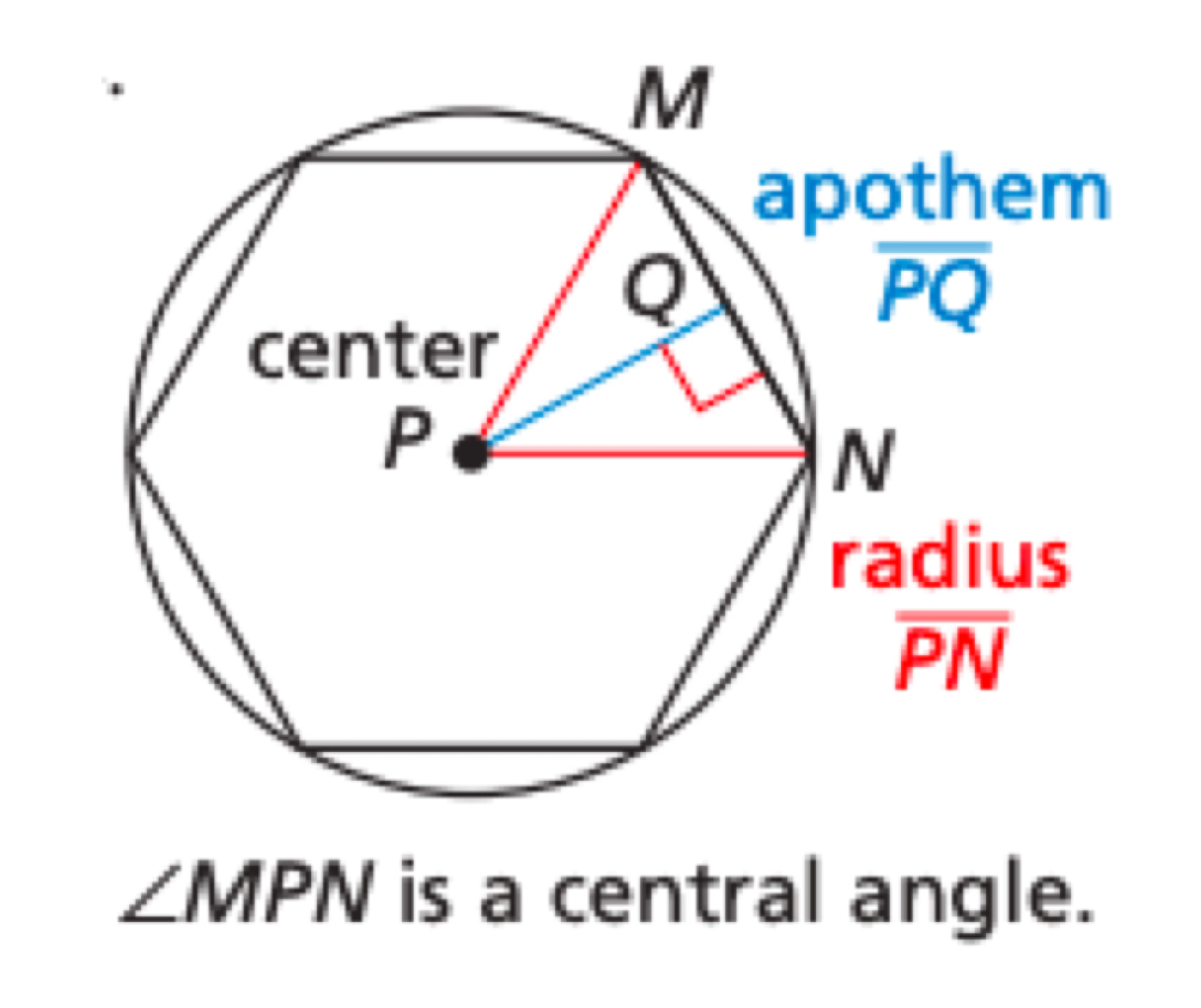
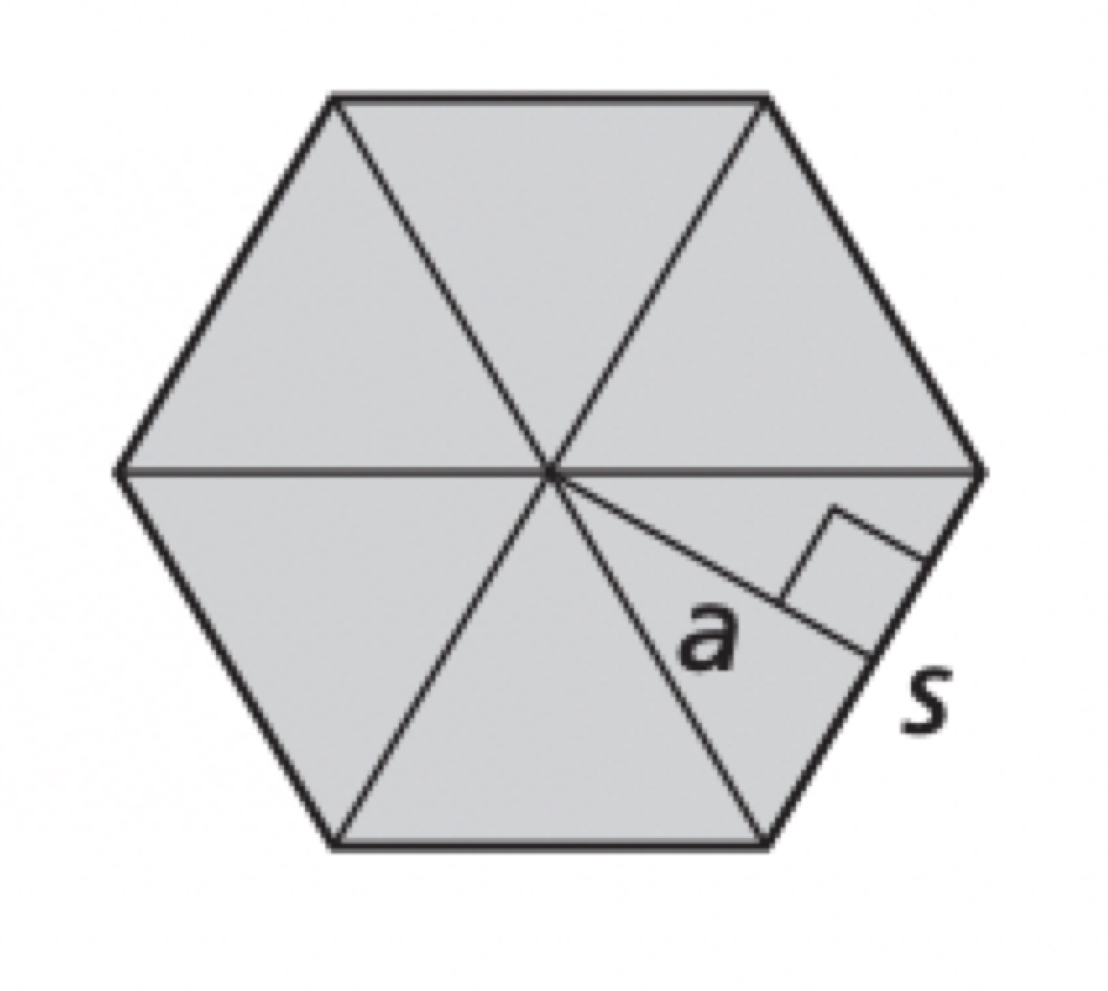
Apothem of a Regular Polygon

The distance from the center to any side of a regular polygon, the height to the base of an isosceles triangle that has two radii as legs, refers to a segment as well as a length

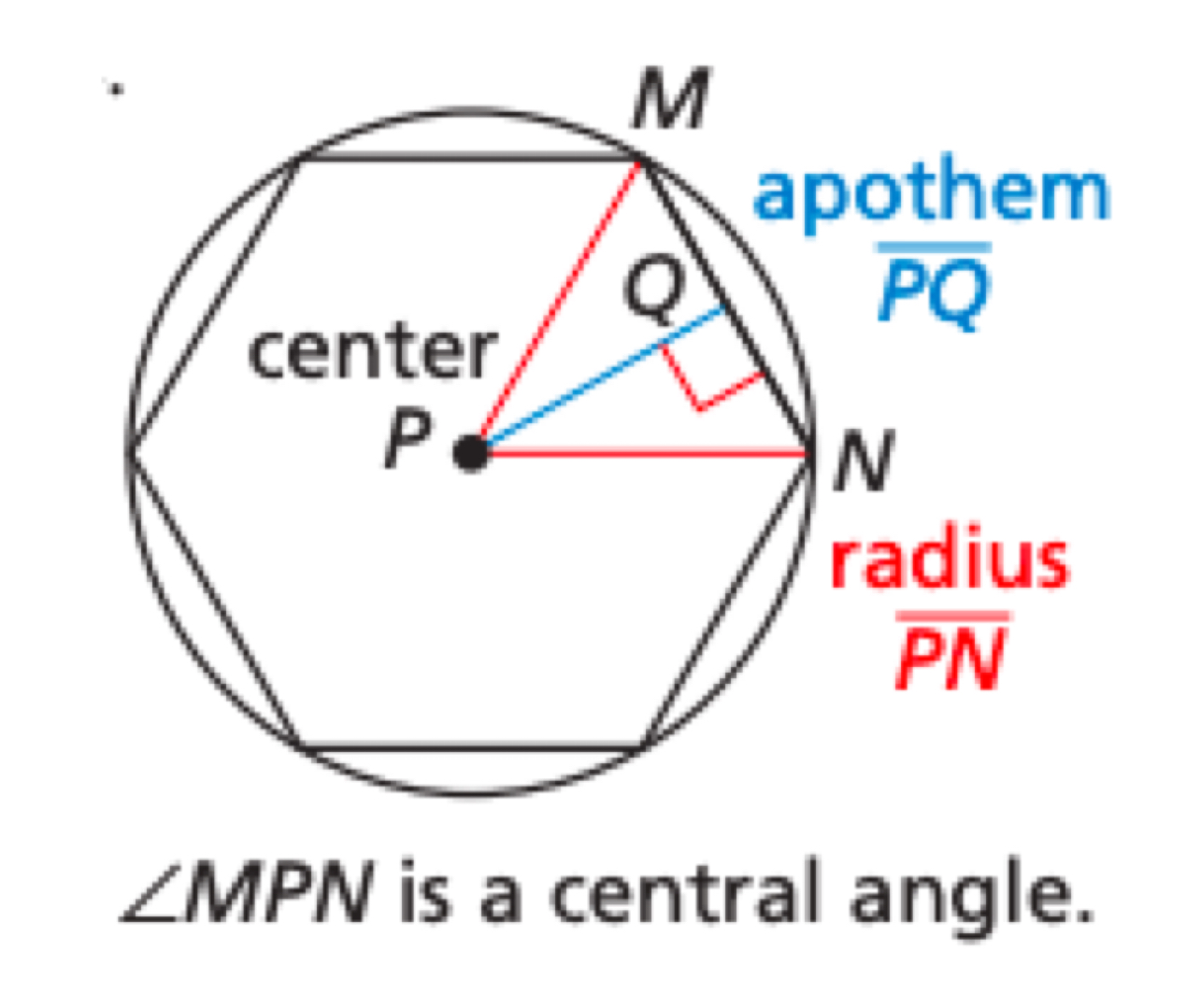
Central Angle of a Regular Polygon

An angle formed by two radii drawn to consecutive vertices of the polygon. To find the measure of each central angle, divide 360º by the number of sides.

Area of a Regular Polygon

The area of a regular n-gon with side length s is one-half the product of the apothem a and the perimeter P. A = 1/2aP, or A = 1/2a • ns

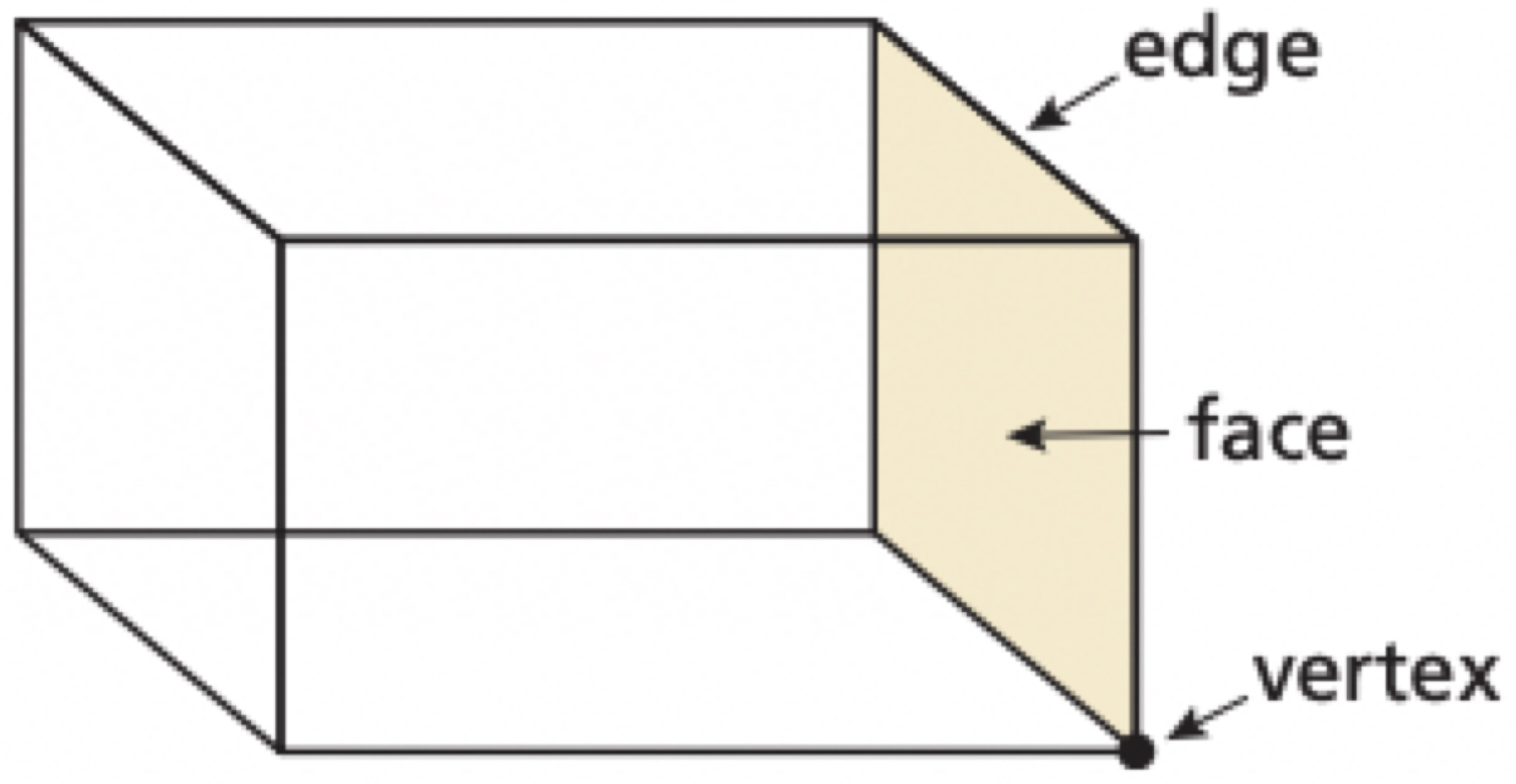
Polyhedron

A solid that is bounded by polygons, called faces. Plural: polyhedra or polyhedrons

Polyhedra

Prism, pyramid

Not polyhedra

Cylinder, cone, sphere

The Five Platonic Solids

Solids that have congruent regular polygons as faces

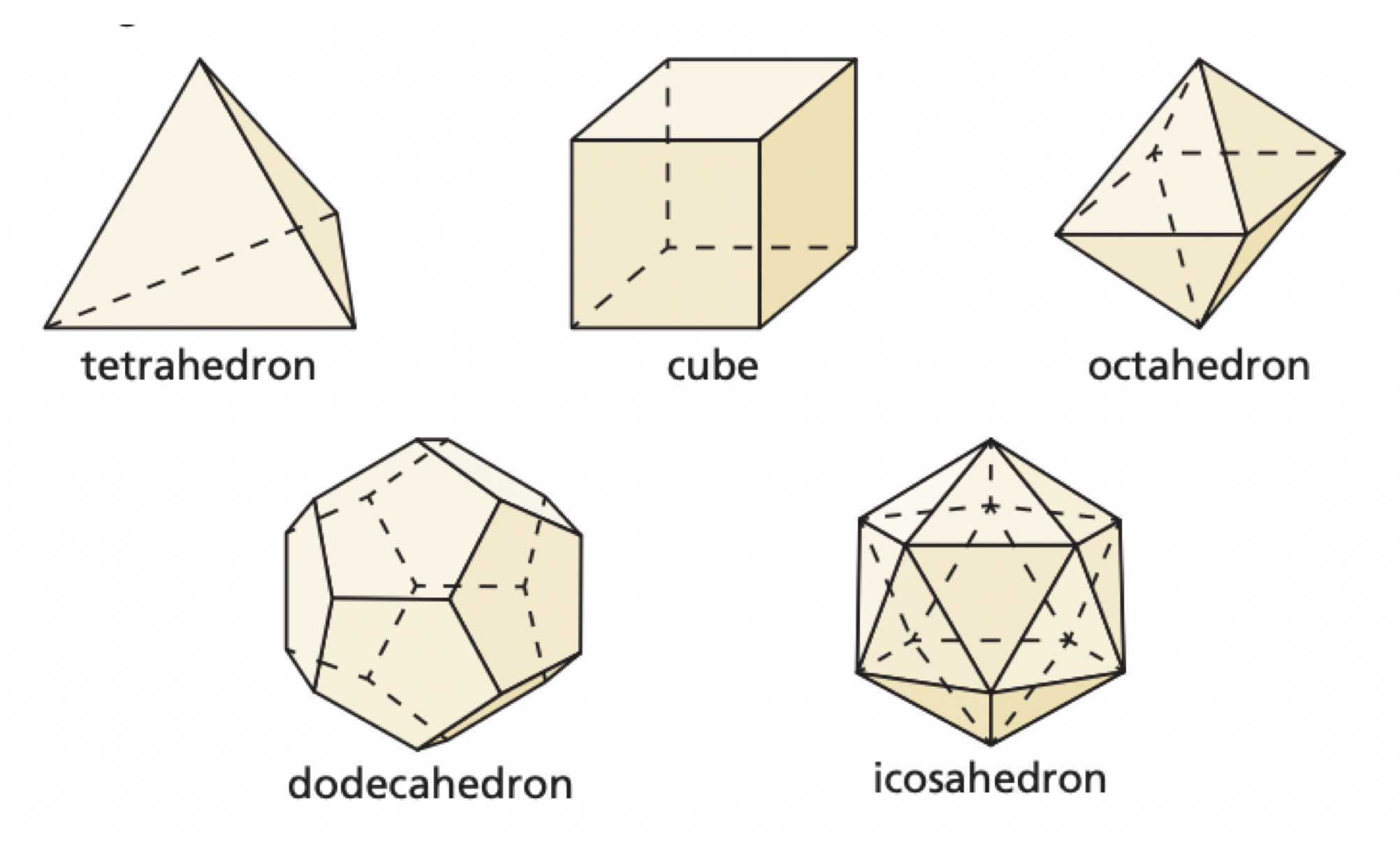
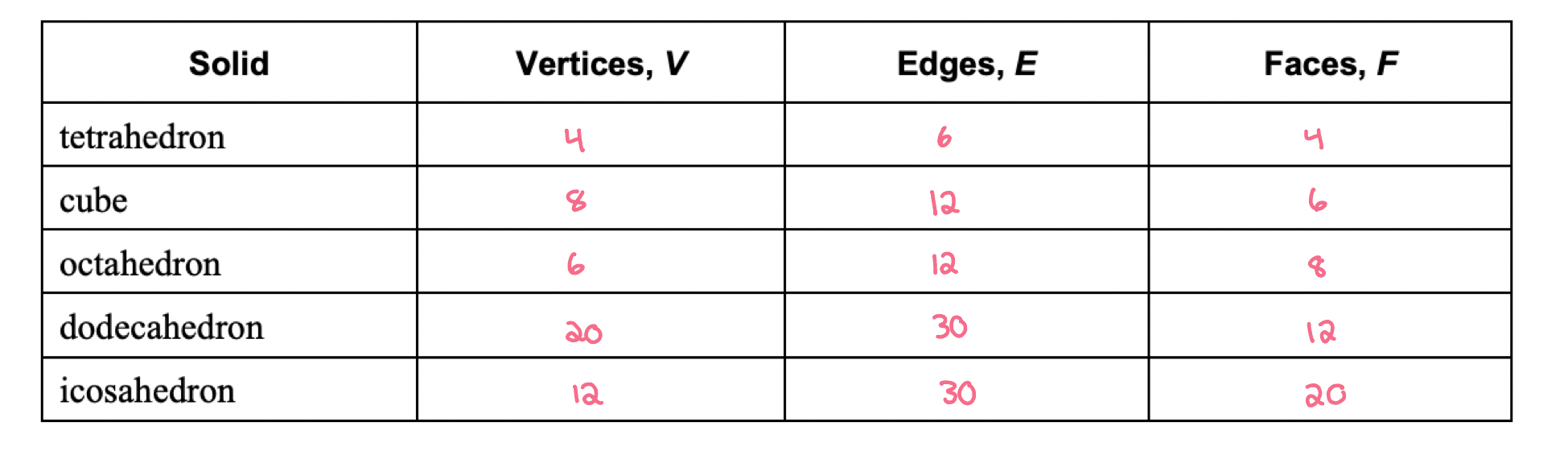
How many vertices, edges, and faces each Platonic solid has

How to name a prism or pyramid

Use the shape of its base

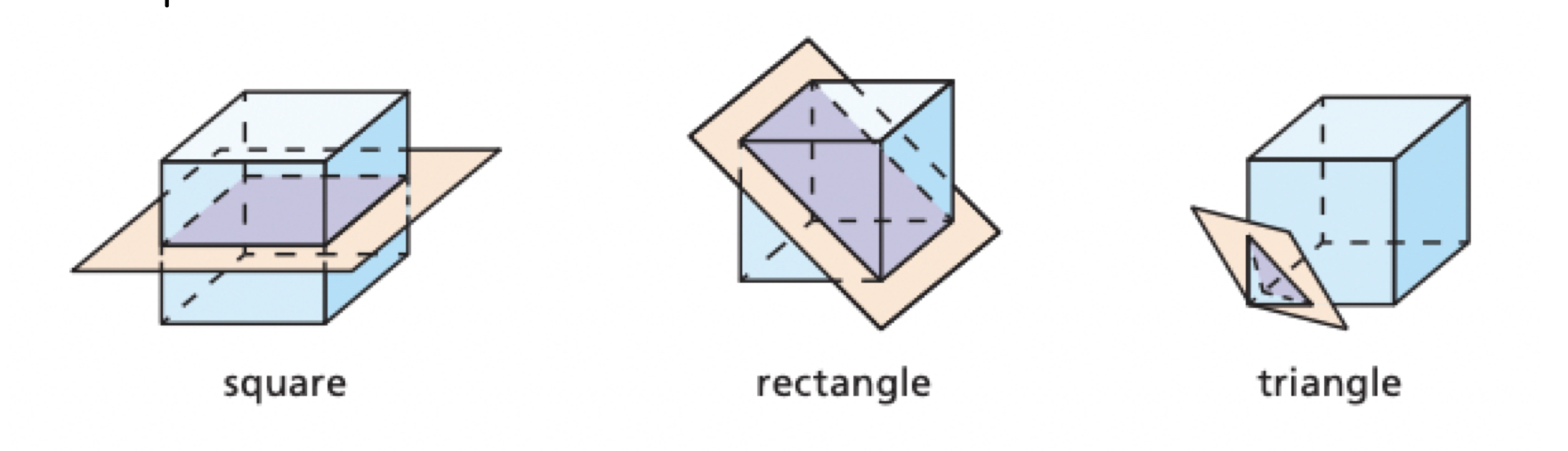
Cross section

The intersection of a plane and a solid

Volume of a Solid

The number of cubic units contained in a solid’s interior

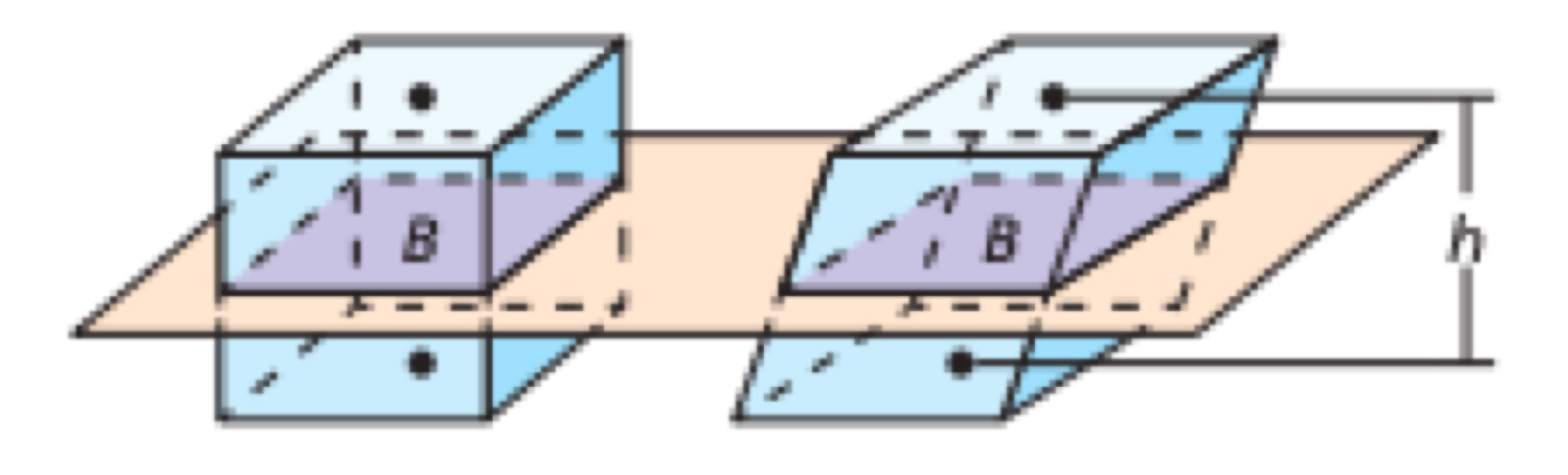
Cavalieri’s Principle

If two solids have the same height and the same cross-sectional area at every level, then they have the same volume

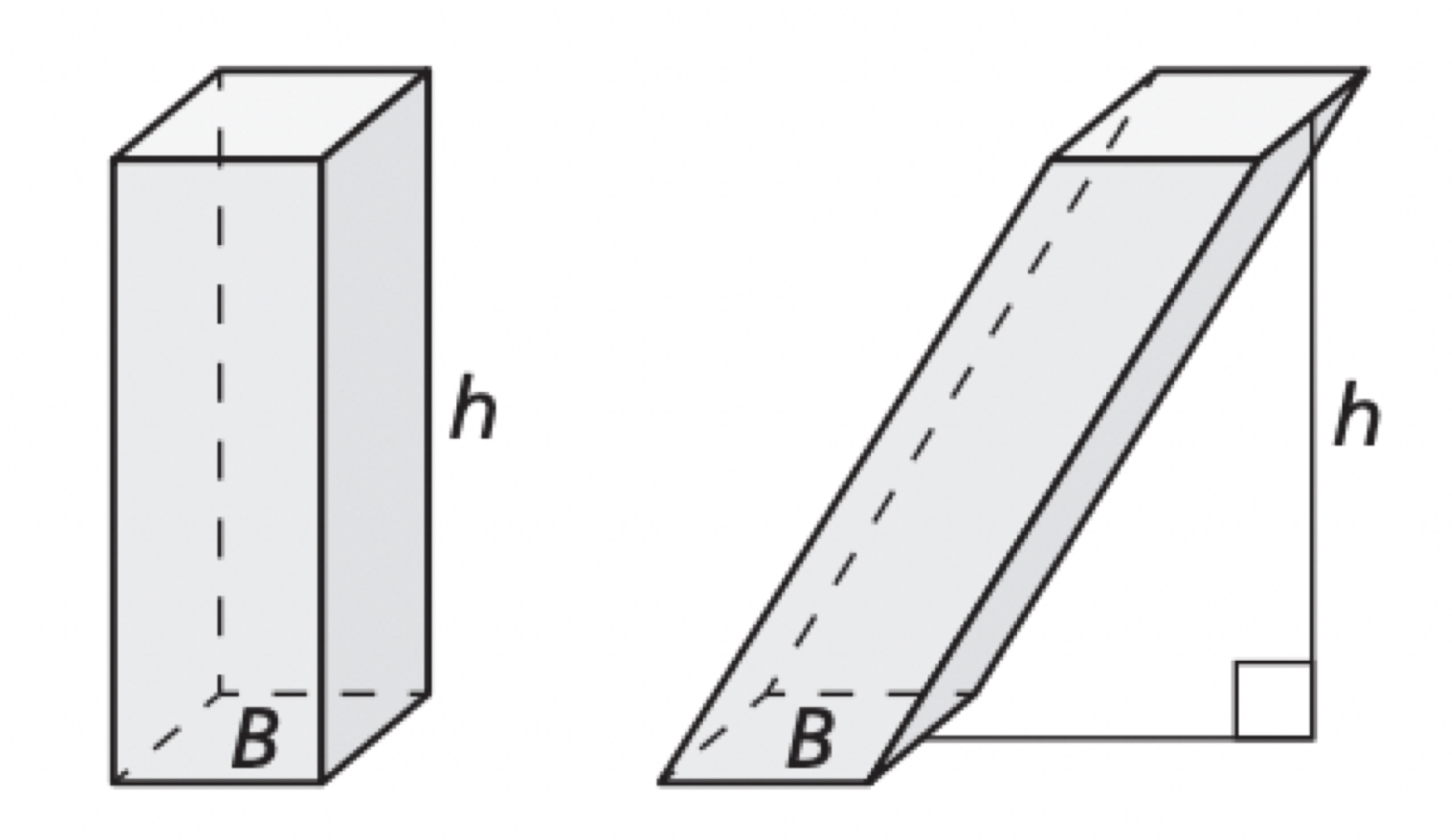
Volume of a Prism

V=Bh where B is the area of the base and h is the height

Volume of a Cylinder

V = Bh = πr²h where B is the area of the base, h is the height, and r is the radius

Density

The amount of matter that an object has in a given unit of volume (mass / volume)

Similar Solids

Two solids of the same type with equal ratios of corresponding linear measures, such as heights or radii. The ratio of the corresponding linear measures of two similar solids is called the scale factor. If two similar solids have a scale factor of k, then the ratio of their volumes is equal to k³

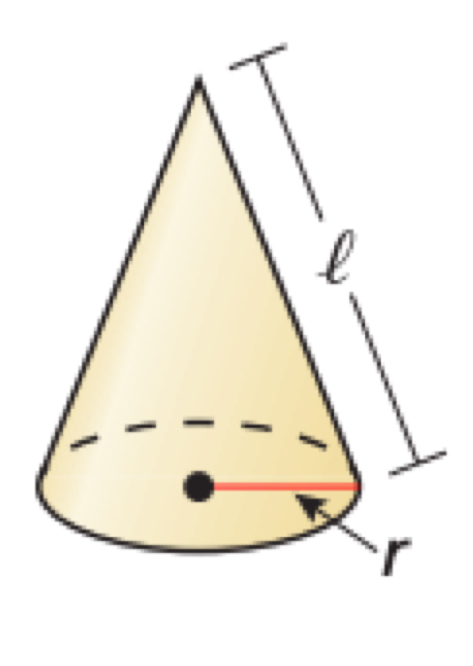
Parts of a Cone

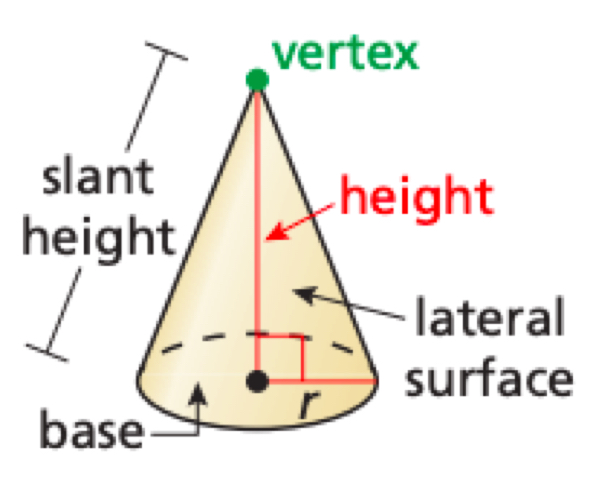
Surface Area of a Right Cone

S = πr² + πrl where r is the radius of the base and l is the slant height

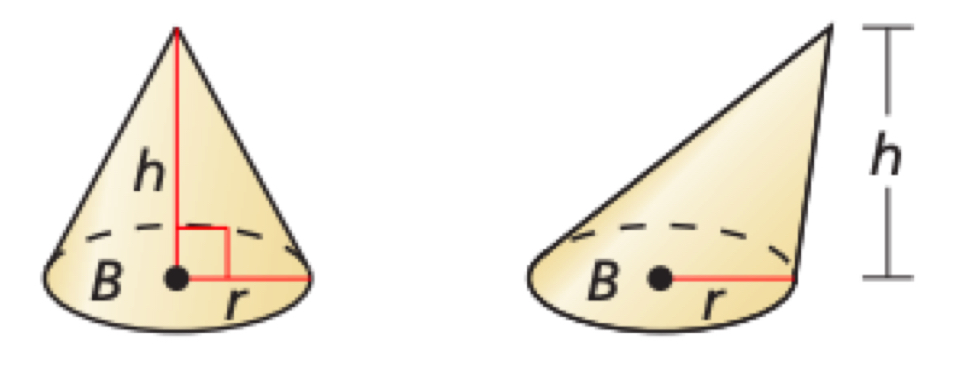
Volume of a Cone

V = 1/3 Bh = 1/3 πr²h

Surface Area of a Sphere

S = 4πr²

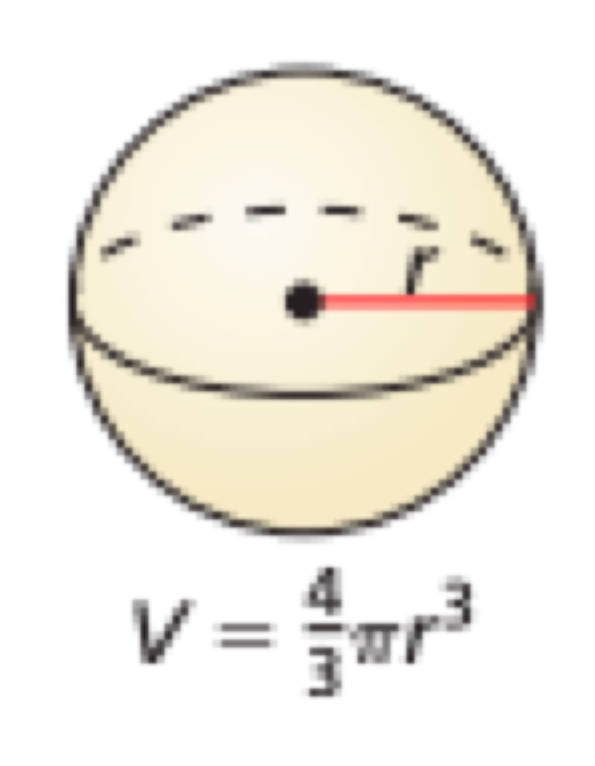
Volume of a Sphere

V = 4/3πr³